Java 数据结构与算法系列精讲之汉诺塔

概述

从今天开始, 小白我将带大家开启 Java 数据结构 & 算法的新篇章.

汉诺塔

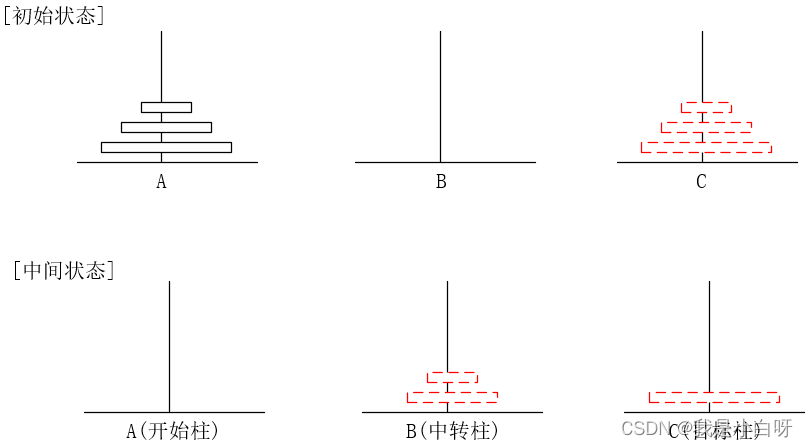
汉诺塔 (Tower of Hanoi) 是一个源于印度的古老益智玩具. 汉诺塔由三根柱子和若干大小不同的圆盘组成. 目标是把圆盘从最左边的柱子移到最右边的柱子上. 如图:

递归

递归 (Recursion) 指的是在函数中调用自身. 递归可以帮助我们简化问题, 使用更少的代码达成目标.

汉诺塔实现

public class 汉诺塔 {

    // 汉诺塔实现
    private static void hanoi(int num, char a, char b, char c) {
        String str = "";

        // 判断是否为最后
        if(num==1) {
            str = "盘1从: " + a + "->" + c;
            System.out.println(str);
        } else {

            // 2^(n-1)次, 把除第n个盘从A移动到B
            hanoi(num - 1, a, c, b);

            str = "盘" + num + "从: " + a + "->" + c;
            System.out.println(str);

            // 2^(n-1)次, 把除第n个盘从B移动到C
            hanoi(num - 1, b, a, c);
        }
    }

    // main
    public static void main(String[] args) {
        hanoi(3, 'A', 'B', 'C');
    }
}

输出结果:

盘1从: A->C
盘2从: A->B
盘1从: C->B
盘3从: A->C
盘1从: B->A
盘2从: B->C
盘1从: A->C

到此这篇关于Java 数据结构与算法系列精讲之汉诺塔的文章就介绍到这了,更多相关Java 汉诺塔内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • JAVA数据结构之汉诺塔代码实例

    本文实例为大家分享了JAVA数据结构之汉诺塔的具体代码,供大家参考,具体内容如下 package p02.动态链表; import p01.动态数组.Stack; public class LinkedStack<E> implements Stack<E> { private LinkedList<E> list; public LinkedStack(){ list=new LinkedList<>(); } @Override public void

  • Java编程用栈来求解汉诺塔问题的代码实例（非递归）

    [题目] 汉诺塔问题比较经典,这里修改一下游戏规则:现在限制不能从最左侧的塔直接移动到最右侧,也不能从最右侧直接移动到最左侧,而是必须经过中间.求当塔有N层的时候,打印最优移动过程和最优移动总步数. [解答] 上一篇用的是递归的方法解决这个问题,这里我们用栈来模拟汉诺塔的三个塔,也就是不用递归的方法 原理是这样的:修改后的汉诺塔问题不能让任何塔从左直接移动到右,也不能从右直接移动到左,而是要经过中间,也就是说,实际上能做的动作,只有四个:左->中,中->左,中->右,右->中 用栈

  • java基于递归算法实现汉诺塔问题实例

    本文实例讲述了java基于递归算法实现汉诺塔问题.分享给大家供大家参考,具体如下: package test; import java.util.List; import java.util.ArrayList; import java.util.Scanner; import sun.net.www.content.audio.x_aiff; /** * @author 年浩 * */ public class test { public static void move(char x,cha

  • Java基于栈方式解决汉诺塔问题实例【递归与非递归算法】

    Java基于栈方式解决汉诺塔问题实例【递归与非递归算法】

    本文实例讲述了Java基于栈方式解决汉诺塔问题.分享给大家供大家参考,具体如下: /** * 栈方式非递归汉诺塔 * @author zy * */ public class StackHanoi { /** * @param args */ public static void main(String[] args) { System.out.println("我们测试结果:"); System.out.println("递归方式:"); hanoiNormal(

  • 手把手带你用java搞定汉诺塔

    手把手带你用java搞定汉诺塔

    目录 什么是汉诺塔 问题剖析 n=1 n=2 n=3 小结 Java代码实现 代码讲解 move函数 hanoiTower函数 附:C语言实现汉诺塔 总结 什么是汉诺塔 汉诺塔问题是一个经典的问题.汉诺塔(Hanoi Tower),又称河内塔,源于印度一个古老传说. 大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘. 大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上.并且规定,任何时候,在小圆盘上都不能放大圆盘,且在三根柱子之间一次只能移

  • Java递归来实现汉诺塔游戏,注释详细

    Java递归来实现汉诺塔游戏,注释详细

    我们很容易能想到,可以用递归来实现汉诺塔游戏.因为要将n(n>1)个盘子从"源"柱子移到"目标"柱子,我们要先把n-1个盘子从"源"柱子移到"辅助"柱子上,然后把最底下那一个盘子移到目标柱子上,最后把"辅助柱"上的n-1个盘子移动到目标柱子上.n==1时直接移到目标柱上,也是递归的出口. 有了以上思路的铺垫,就可以开始实现代码了. public class HanoiDemo { public sta

  • java递归实现汉诺塔步骤介绍

    java递归实现汉诺塔步骤介绍

    汉诺塔的规则是:一共三根柱子,一根柱子从上到下套着有小到大的若干个圆盘,要将所有圆盘按照这个排放顺序移动到第三根柱子上,并且每次只能移动一个圆盘. 可以将整个过程分为三个步骤来看: 第一步:将除最大圆盘外的n-1个圆盘移动辅助柱子上 第二步:将最大的圆盘移动到目标柱子 第三步:将n-1个圆盘从辅助柱子移动到目标柱子 其中第一步又可以拆成一模一样的三步,可以看成一个n-1层的塔要移动到目标柱子,只不过目标柱子换了一个: 第三步也可以拆分成一模一样的三步: 多拆几次就会发现规律:第一步和第三步无论如

  • Java 实现一个汉诺塔实战练习

    Java 实现一个汉诺塔实战练习

    汉诺塔简介: 我们想要实现的是 让 A柱上的盘子,移动到C柱上 1层汉诺塔 2层汉诺塔 3层汉诺塔详解图 第一步 第二步 第三步 第四步 第五步 第六步 第七步 经过上面的图解,相比大家一定在一定程度了解到汉诺塔的游戏规则,以及怎么去玩. 总之 最终C柱上第一个盘子,是最大,最顶的是最小的,而且在操作过程中,前几步就是为了让三个柱子中最大的盘子移动到C柱上, 然后不断,将它两个柱子中最大盘子往上累加,(盘子从大到小,从下往上摆放) 而且盘子一多,你就会发现过程中间,除了最大的盘子,其余的盘子都会

  • Java手把手必会的实例汉诺塔讲解练习

    Java手把手必会的实例汉诺塔讲解练习

    最适合菜鸟的汉诺塔讲解 问题引入 汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘.大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上.并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘. 让我们先从小事入手. 标记汉诺塔的三根柱子分别为 a ,b ,c 标记汉诺塔上的圆盘分别为:1 ,2,3,4 -n a 柱上面只有一个圆盘时 只有这一种走法 a柱上有两个圆盘时

  • Java 数据结构与算法系列精讲之汉诺塔

    Java 数据结构与算法系列精讲之汉诺塔

    概述 从今天开始, 小白我将带大家开启 Java 数据结构 & 算法的新篇章. 汉诺塔 汉诺塔 (Tower of Hanoi) 是一个源于印度的古老益智玩具. 汉诺塔由三根柱子和若干大小不同的圆盘组成. 目标是把圆盘从最左边的柱子移到最右边的柱子上. 如图: 递归 递归 (Recursion) 指的是在函数中调用自身. 递归可以帮助我们简化问题, 使用更少的代码达成目标. 汉诺塔实现 public class 汉诺塔 { // 汉诺塔实现 private static void hanoi(i

  • Java 数据结构与算法系列精讲之贪心算法

    Java 数据结构与算法系列精讲之贪心算法

    概述 从今天开始, 小白我将带大家开启 Java 数据结构 & 算法的新篇章. 贪心算法 贪心算法 (Greedy Algorithm) 指的是在每一步选择中都采取在当前状态下最好或最优的选择, 从而希望导致结果是最好或最优的算法. 贪心算法锁得到的结果不一定是最优的结果, 但是都是相对近似最优的结果. 贪心算法的优缺点: 优点: 贪心算法的代码十分简单 缺点: 很难确定一个问题是否可以用贪心算法解决 电台覆盖问题 假设存在以下的广播台, 以及广播台可以覆盖的地区: 广播台 覆盖地区 K1 北京

  • Java 数据结构与算法系列精讲之排序算法

    Java 数据结构与算法系列精讲之排序算法

    概述 从今天开始, 小白我将带大家开启 Java 数据结构 & 算法的新篇章. 冒泡排序 冒泡排序 (Bubble Sort) 是一种简单的排序算法. 它重复地遍历要排序的数列, 一次比较两个元素, 如果他们的顺序错误就把他们交换过来. 遍历数列的工作是重复地进行直到没有再需要交换, 也就是说该数列已经排序完成. 这个算法的名字由来是因为越小的元素会经由交换慢慢 "浮" 到数列的顶端. 冒泡排序流程: 通过比较相邻的元素, 判断两个元素位置是否需要互换 进行 n-1 次比较,

  • Java 数据结构与算法系列精讲之KMP算法

    Java 数据结构与算法系列精讲之KMP算法

    概述 从今天开始, 小白我将带大家开启 Java 数据结构 & 算法的新篇章. KMP 算法 KMP (Knuth-Morris-Pratt), 是一种改进的字符串匹配算法. KMP 算法解决了暴力匹配需要高频回退的问题, KMP 算法在匹配上若干字符后, 字符串位置不需要回退, 从而大大提高效率. 如图: 举个例子 (字符串 "abcabcdef" 匹配字符串 "abcdef"): 次数 暴力匹配 KMP 算法 说明 1 abcabcdef abcdef

  • Java 数据结构与算法系列精讲之字符串暴力匹配

    Java 数据结构与算法系列精讲之字符串暴力匹配

    概述 从今天开始, 小白我将带大家开启 Java 数据结构 & 算法的新篇章. 字符串匹配 字符串匹配 (String Matching) 指的是判断一个字符串是否包含另一个字符串. 举个例子: 字符串 "Hello World" 包含字符串 "Hello" 字符串 "Hello World" 不包含字符串 "LaLaLa" 暴力匹配 暴力匹配 (Brute-Force) 的思路: 如果charArray1[i] ==

  • Java 数据结构与算法系列精讲之单向链表

    Java 数据结构与算法系列精讲之单向链表

    目录 概述 链表 单向链表 单向链表实现 Node类 add方法 remove方法 get方法 set方法 contain方法 main 完整代码 概述 从今天开始, 小白我将带大家开启 Jave 数据结构 & 算法的新篇章. 链表 链表 (Linked List) 是一种递归的动态数据结构. 链表以线性表的形式, 在每一个节点存放下一个节点的指针. 链表解决了数组需要先知道数据大小的缺点, 增加了节点的指针域, 空间开销较大. 链表包括三类: 单向链表 双向链表 循环链表 单向链表 单向链表

  • Java 数据结构与算法系列精讲之环形链表

    Java 数据结构与算法系列精讲之环形链表

    目录 概述 链表 环形链表 环形链表实现 Node类 insert方法 remove方法 main 完整代码 概述 从今天开始, 小白我将带大家开启 Java 数据结构 & 算法的新篇章. 链表 链表 (Linked List) 是一种递归的动态数据结构. 链表以线性表的形式, 在每一个节点存放下一个节点的指针. 链表解决了数组需要先知道数据大小的缺点, 增加了节点的指针域, 空间开销较大. 链表包括三类: 单向链表 双向链表 循环链表 环形链表 环形链表 (Circular Linked Li

  • Java 数据结构与算法系列精讲之栈

    Java 数据结构与算法系列精讲之栈

    目录 概述 栈 栈实现 push方法 pop方法 main 完整代码 概述 从今天开始, 小白我将带大家开启 Jave 数据结构 & 算法的新篇章. 栈 栈 (Stack) 是一种运算受限的线性表, 遵循先进后出的原则 (Last-In-First-Out). 举个例子, 当我们灌调料的时候, 后灌进去的调料会先被使用. 栈只能在表尾部进行插入和删除的操作. 开口的一端被称为栈顶, 另一端则被称为栈底. 如图: 栈实现 push 方法 栈 (Stack) 的 push 方法, 把项压入栈顶部.

  • Java 数据结构与算法系列精讲之数组

    Java 数据结构与算法系列精讲之数组

    目录 概述 数组 声明数组的两个方法 创建数组的两个方法 索引 自定义数组 泛型 构造函数 元素操作 调用 完整代码 概述 从今天开始, 小白我将带大家开启 Jave 数据结构 & 算法的新篇章. 数组 数组 (Array) 是有序数据的集合, 在 Java 中 java.util.Arrays包含用来操作数组的各种方法, 比如排序和搜索等. 其所有方法均为静态方法, 调用起来非常简单. 声明数组的两个方法 方法一: 数据类型[] array; 方法二: 数据类型 array[]; 创建数组的两

  • Java 数据结构与算法系列精讲之二叉堆

    Java 数据结构与算法系列精讲之二叉堆

    目录 概述 优先队列 二叉堆 二叉堆实现 获取索引 添加元素 siftUp 完整代码 概述 从今天开始, 小白我将带大家开启 Java 数据结构 & 算法的新篇章. 优先队列 优先队列 (Priority Queue) 和队列一样, 是一种先进先出的数据结构. 优先队列中的每个元素有各自的优先级, 优先级最高的元素最先得到服务. 如图: 二叉堆 二叉堆 (Binary Heap) 是一种特殊的堆, 二叉堆具有堆的性质和二叉树的性质. 二叉堆中的任意一节点的值总是大于等于其孩子节点值. 如图: 二

随机推荐