Python实现高斯函数的三维显示方法

在网上查阅资料，发现很少用Python进行高斯函数的三维显示绘图的，原因可能是其图形显示太过怪异，没有MATLAB精细和直观。

回顾一下二维高斯公式：

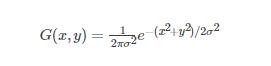
σ此处取3。

在MATLAB下的程序为：

u=[-10:0.1:10];
v=[-10:0.1:10];
[U,V]=meshgrid(u,v);
H=exp(-(U.^2+V.^2)./2/3^2);
mesh(u,v,H); %绘制三维曲面的函数
title('高斯函数曲面');

其显示结果为：

放大效果显示，很平滑和直观。

以下为Python的程序部分：

import numpy as np
import matplotlib.pyplot as plt
import math
import mpl_toolkits.mplot3d

x, y = np.mgrid[-2:2:200j, -2:2:200j]
z=(1/2*math.pi*3**2)*np.exp(-(x**2+y**2)/2*3**2)
ax = plt.subplot(111, projection='3d')
ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap='rainbow', alpha=0.9)#绘面

ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()

显示效果：

以上这篇Python实现高斯函数的三维显示方法就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。

赞 (0)

相关推荐

  • Python最小二乘法矩阵

    最小二乘法矩阵 #! /usr/bin/env python # -*- coding: utf-8 -*- import numpy as np def calc_left_k_mat(k): """ 获得左侧k矩阵 :param k: :return: """ k_mat = [] for i in range(k + 1): now_line = [] for j in range(k + 1): now_line.append(j + i

  • 对Python的zip函数妙用,旋转矩阵详解

    Python的zip函数 示例1: x = [1, 2, 3] y = [4, 5, 6] z = [7, 8, 9] xyz = zip(x, y, z) print xyz 运行的结果是: [(1, 4, 7), (2, 5, 8), (3, 6, 9)] 从这个结果可以看出zip函数的基本运作方式. 示例2: x = [1, 2, 3] y = [4, 5, 6] z = [7, 8, 9] xyz = zip(x, y, z) u = zip(*xyz) print u 运行的结果是:

  • python for循环输入一个矩阵的实例

    代码如下: a=[] for i in range(3): a.append([]) for j in range(3): a[i].append(int(input('输入整数:\n'))) print(a) 结果如下: 输入整数: 1 输入整数: 2 输入整数: 3 输入整数: 4 输入整数: 5 输入整数: 6 输入整数: 7 输入整数: 8 输入整数: 9 [[1, 2, 3], [4, 5, 6], [7, 8, 9]] 以上这篇python for循环输入一个矩阵的实例就是小编分享给

  • Python高斯消除矩阵

    高斯消除矩阵 #! /usr/bin/env python # -*- coding: utf-8 -*- # def pprint(A): for i in A: print(i) print("") data = [ [1, 2, 1, 2], [3, 8, 1, 12], [0, 4, 1, 2] ] n = len(data) print("输入数据") pprint(data) for i in range(n): print("第{}次操作&q

  • python 顺时针打印矩阵的超简洁代码

    如下所示: # -*- coding:utf-8 -*- class Solution: # matrix类型为二维列表,需要返回列表 def printMatrix(self, matrix): # write code here res=[] n=len(matrix) m=len(matrix[0]) if m==1 and n==1: res=[matrix[0][0]] return res else: for o in range((min(m,n)+1)//2): [res.app

  • Python基于高斯消元法计算线性方程组示例

    本文实例讲述了Python基于高斯消元法计算线性方程组.分享给大家供大家参考,具体如下: #!/usr/bin/env python # coding=utf-8 # 以上的信息随自己的需要改动吧 def print_matrix( info, m ): # 输出矩阵 i = 0; j = 0; l = len(m) print info for i in range( 0, len( m ) ): for j in range( 0, len( m[i] ) ): if( j == l ):

  • python+opencv实现高斯平滑滤波

    python+opencv实现高斯平滑滤波

    功能: 创建两个滑动条来分别控制高斯核的size和σσ的大小,这个程序是在阈值分割的那个程序上改动的.阈值分割程序在这 注意:由于σ=0σ=0时,opencv会根据窗口大小计算出σσ,所以,从0滑动σσ的滑动条时,会出现先边清晰又变模糊的现象 python+opencv实现阈值分割 python+opencv实现霍夫变换检测直线 (2016-5-10)到OpenCV-Python Tutorials's documentation!可以下载 代码: # -*- coding: utf-8 -*-

  • 在Python中使用PIL模块对图片进行高斯模糊处理的教程

    在Python中使用PIL模块对图片进行高斯模糊处理的教程

    从一篇文章中看到,PIL 1.1.5 已经内置了高斯模糊,但是并没有在文档中提及,而且PIL的高斯模糊中 radius 是硬编码, 虽然构造方法中有传入 radius 参数,但压根就没有用到 (看这里),所以需要自己进行改造,当然,知道了原因, 修改起来自然非常简单了. 结合帖子中的需求,对局部进行高斯模糊,所以还需要结合使用 crop和 paste 方法实现局部使用滤镜. 代码如下: #-*- coding: utf-8 -*- from PIL import Image, ImageFilt

  • python矩阵的转置和逆转实例

    如下所示: # 矩阵的转置 def transpose(list1): return [list(row) for row in zip(*list1)] list1 = [[1, 4], [2, 5], [3, 6]] print(transpose(list1)) # [[1, 2, 3], [4, 5, 6]] 矩阵转置 用zip将一系列可迭代对象中的元素打包为元组,之后将这些元组放置在列表中,两步加起来等价于行列转置. # 矩阵逆转 def invert(list1): return [

  • Python中使用PIL库实现图片高斯模糊实例

    Python中使用PIL库实现图片高斯模糊实例

    一.安装PIL PIL是Python Imaging Library简称,用于处理图片.PIL中已经有图片高斯模糊处理类,但有个bug(目前最新的1.1.7bug还存在),就是模糊半径写死的是2,不能设置.在源码ImageFilter.py的第160行: 所以,我们在这里自己改一下就OK了. 项目地址:http://www.pythonware.com/products/pil/ 二.修改后的代码 代码如下: 复制代码 代码如下: #-*- coding: utf-8 -*- from PIL

随机推荐