哈夫曼算法构造代码

1.定义

　　哈夫曼编码主要用于数据压缩。

　　哈夫曼编码是一种可变长编码。该编码将出现频率高的字符，使用短编码；将出现频率低的字符，使用长编码。

　　变长编码的主要问题是，必须实现非前缀编码，即在一个字符集中，任何一个字符的编码都不是另一个字符编码的前缀。如：0、10就是非前缀编码，而0、01不是非前缀编码。

2.哈夫曼树的构造

　　按照字符出现的频率，总是选择当前具有较小频率的两个节点，组合为一个新的节点，循环此过程知道只剩下一个节点为止。

　　对于5个字符A、B、C、D、E，频率分别用1、5、7、9、6表示，则构造树的过程如下：

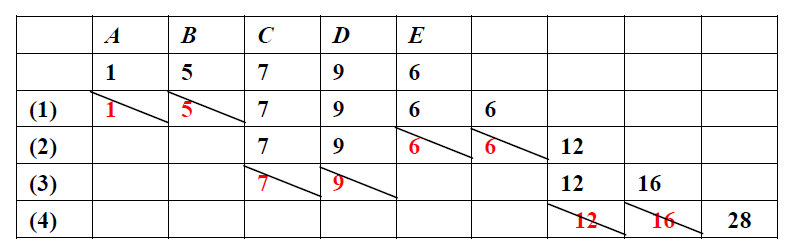
上面过程对应的哈夫曼树为：

假设规定左边为0，右边为1，则变长编码为：

　　A 1:010

　　B 5:011

　　C 7:10

　　D 9:11

　　E 6: 00

3.哈夫曼构造代码

代码如下:

#include <iostream>
#include <string.h>
using namespace std;
struct Node{
    char c;
    int value;
    int par;
    char tag;    //tag='0',表示左边；tag='1'，表示右边
    bool isUsed;    //判断这个点是否已经用过
    Node(){
        par=-1;
        isUsed=false;
    }
};

int input(Node*,int);   //输入节点信息
int buildedTree(Node*,int); //建哈夫曼树
int getMin(Node*,int);  //寻找未使用的，具有最小频率值的节点
int outCoding(Node*,int);   //输出哈夫曼编码

int main ()
{
    int n;
    cin>>n;
    Node *nodes=new Node[2*n-1];
    input(nodes,n);
    buildedTree(nodes,n);
    outCoding(nodes,n);
    delete(nodes);
    return 0;
}

int input(Node* nodes,int n){
    for(int i=0;i<n;i++){
        cin>>(nodes+i)->c;
        cin>>(nodes+i)->value;
    }
    return 0;
}

int buildedTree(Node* nodes,int n){
    int last=2*n-1;
    int t1,t2;
    for(int i=n;i<last;i++){
        t1=getMin(nodes,i);
        t2=getMin(nodes,i);
        (nodes+t1)->par=i; (nodes+t1)->tag='0';
        (nodes+t2)->par=i; (nodes+t2)->tag='1';
        (nodes+i)->value=(nodes+t1)->value+(nodes+t2)->value;
    }
    return 0;
}

int getMin(Node* nodes,int n){
    int minValue=10000000;
    int pos=0;
    for(int i=0;i<n;i++)
    {
        if((nodes+i)->isUsed == false && (nodes+i)->value<minValue){
            minValue=(nodes+i)->value;
            pos=i;
        }
    }
    (nodes+pos)->isUsed=true;
    return pos;
}

int outCoding(Node* nodes,int n){
    char a[100];
    int pos,k,j;
    char tmp;
    for(int i=0;i<n;i++){
        k=0;
        pos=i;
        memset(a,'\0',sizeof(a));
        while((nodes+pos)->par!=-1){
            a[k++]=(nodes+pos)->tag;
            pos=(nodes+pos)->par;
        }
        strrev(a);    //翻转字符串
        cout<<(nodes+i)->c<<" "<<(nodes+i)->value<<":"<<a<<endl;
    }
    return 0;
}

执行示例：