JS使用Dijkstra算法求解最短路径

一、Dijkstra算法的思路

Dijkstra算法是针对单源点求最短路径的算法。

其主要思路如下：

1. 将顶点分为两部分：已经知道当前最短路径的顶点集合Q和无法到达顶点集合R。

2. 定义一个距离数组（distance）记录源点到各顶点的距离，下标表示顶点，元素值为距离。源点（start）到自身的距离为0，源点无法到达的顶点的距离就是一个大数（比如Infinity）。

3. 以距离数组中值为非Infinity的顶点V为中转跳点，假设V跳转至顶点W的距离加上顶点V至源点的距离还小于顶点W至源点的距离，那么就可以更新顶点W至源点的距离。即下面distance[V] + matrix[V][W] < distance[W]，那么distance[W] = distance[V] + matrix[V][W]。

4. 重复上一步骤，即遍历距离数组，同时无法到达顶点集合R为空。

二、具体例子

偷个懒，直接用上一篇博客《最小生成树算法——Prim算法和Kruskal算法的JS实现》的图为例子。

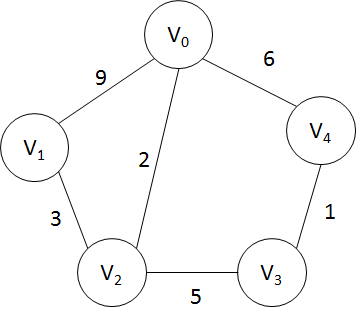
它的邻接矩阵如下：

求解步骤 

第一步：假设源点为V0，那么目前最短路径的顶点集合Q中就只有{V0}和无法到达顶点集合R中有{V1, V2, V3, V4}

第二步：初始化distance数组，就是下面这样

第三步：以distance数组中值为非Infinity的顶点为中转跳点，这一步就是V0，依照如果distance[V] + matrix[V][W] < distance[W]，那么distance[W] = distance[V] + matrix[V][W]的规则，distance数组就会变成下面这样，同时集合Q变成了{V0, V1, V2, V4}，集合R变成了{V3}

第四步：因为集合R中还有1个顶点，所以重复第三步的方法，然后变成以V1为中转跳点，但是以V1为中转顶点都不满足distance[V] + matrix[V][W] < distance[W]，所以没更新distance和两个集合

第五步：因为集合R中还有1个顶点，所以重复第三步的方法，此时变成以V2为中转跳点，然后发现V0到达V3的距离可以更新，因为2 + 3 < 9，所以distance更新，集合也更新。

之后同理，遍历完distance之后，输出

三、代码实现

这个代码没有考虑权值为负数的情况，还没验证负数的情况，目前是按照权值为正数实现的，之后考虑完善。

同时这是针对单源点求最短路径，如果求全图各顶点的最短路径，只需要遍历顶点然后使用Dijkstra算法，这样算上Dijkstra算法本身的时间复杂度，总的复杂度会是O(n^3)。

/**
 * Dijkstra算法：单源最短路径
 * 思路：
 * 1. 将顶点分为两部分：已经知道当前最短路径的顶点集合Q和无法到达顶点集合R。
 * 2. 定义一个距离数组（distance）记录源点到各顶点的距离，下标表示顶点，元素值为距离。源点（start）到自身的距离为0，源点无法到达的顶点的距离就是一个大数（比如Infinity）。
 * 3. 以距离数组中值为非Infinity的顶点V为中转跳点，假设V跳转至顶点W的距离加上顶点V至源点的距离还小于顶点W至源点的距离，那么就可以更新顶点W至源点的距离。即下面distance[V] + matrix[V][W] < distance[W]，那么distance[W] = distance[V] + matrix[V][W]。
 * 4. 重复上一步骤，即遍历距离数组，同时无法到达顶点集合R为空。
 *
 * @param matrix 邻接矩阵，表示图
 * @param start 起点
 *
 *
 *
 * 如果求全图各顶点作为源点的全部最短路径，则遍历使用Dijkstra算法即可，不过时间复杂度就变成O(n^3)了
 * */
function Dijkstra(matrix, start = 0) {
  const rows = matrix.length,//rows和cols一样，其实就是顶点个数
    cols = matrix[0].length;

  if(rows !== cols || start >= rows) return new Error("邻接矩阵错误或者源点错误");

  //初始化distance
  const distance = new Array(rows).fill(Infinity);
  distance[start] = 0;

  for(let i = 0; i < rows; i++) {
    //达到不了的顶点不能作为中转跳点
    if(distance[i] < Infinity) {
      for(let j = 0; j < cols; j++) {
        //比如通过比较distance[i] + matrix[i][j]和distance[j]的大小来决定是否更新distance[j]。
        if(matrix[i][j] + distance[i] < distance[j]) {
          distance[j] = matrix[i][j] + distance[i];
        }
      }
      console.log(distance);
    }
  }
  return distance;
}

/**
 * 邻接矩阵
 * 值为顶点与顶点之间边的权值，0表示无自环，一个大数表示无边(比如10000)
 * */
const MAX_INTEGER = Infinity;//没有边或者有向图中无法到达
const MIN_INTEGER = 0;//没有自环

const matrix= [
  [MIN_INTEGER, 9, 2, MAX_INTEGER, 6],
  [9, MIN_INTEGER, 3, MAX_INTEGER, MAX_INTEGER],
  [2, 3, MIN_INTEGER, 5, MAX_INTEGER],
  [MAX_INTEGER, MAX_INTEGER, 5, MIN_INTEGER, 1],
  [6, MAX_INTEGER, MAX_INTEGER, 1, MIN_INTEGER]
];

console.log(Dijkstra(matrix, 0));//[ 0, 5, 2, 7, 6 ]

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。