pytorch之深度神经网络概念全面整理

目录

• 1、神经网络训练过程
• 2、基础概念
• 2.1数学知识
• 2.1.1导数
• 2.1.2 梯度
• 2.2前向传播和反向传播
• 3、数据预处理手段
• 3.1 归一化  (normalization)
• 3.2 标准化（Standardization）
• 3.3 正则化
• 3.4 独热码编码（one hot）
• 4、数据处理库
• 4.1 numpy
• 4.2 pandas
• 4.3 matplotlib
• 5、训练集、测试集，测试集
• 6、损失函数
• 7、优化器
• 8、激活函数
• 9、hello world
• 10、总结

推荐阅读 点击标题可跳转

1、如何搭建pytorch环境的方法步骤

今天是第一篇文章，希望自己能坚持，加油。

深度神经网络就是用一组函数去逼近原函数，训练的过程就是寻找参数的过程。

1、神经网络训练过程

神经网络的训练过程如下：

• 收集数据，整理数据
• 实现神经网络用于拟合目标函数
• 做一个真实值和目标函数值直接估计误差的损失函数，一般选择既定的损失函数
• 用损失函数值前向输入值求导，
• 再根据导数的反方向去更新网络参数(x),目的是让损失函数值最终为0.，最终生成模型

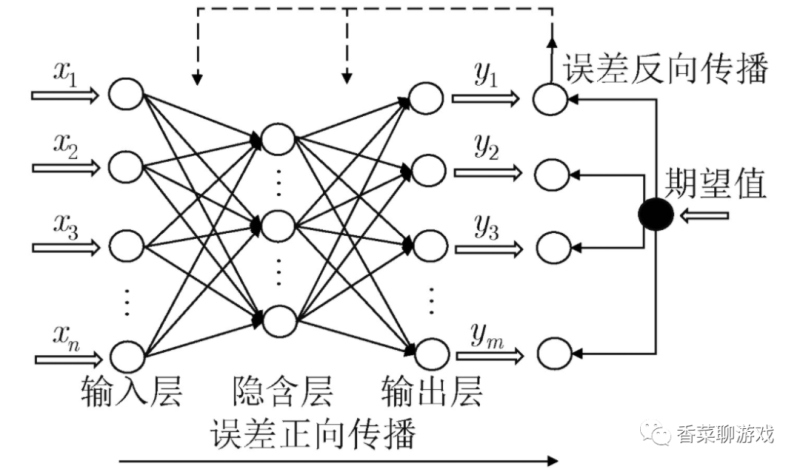
各层概念解释

• 输入层：就是参数输入
• 输出层：就是最后的输出
• 隐藏层（隐含层）：除去其他两层之外的层都可以叫隐藏层

模型是什么：

• 模型包含两部分，一部分是神经网络的结构，一部分是各个参数，最后训练的成果就是这个

2、基础概念

2.1数学知识

2.1.1导数

导数在大学的时候还是学过的，虽然概念很简单，但是过了这么多年几乎也都忘了，连数学符号都不记得了，在复习之后才理解：就是表示数据变化的快慢，是变化率的概念，比如重力加速度，表示你自由落体之后每秒速度的增量。

数学公式是：

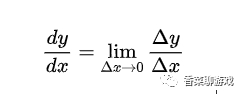
不重要，看不看的懂都行，因为在后面的学习中也不会让你手动求导，框架里都有现成的函数

2.1.2 梯度

梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）

梯度：是一个矢量，其方向上的方向导数最大，其大小正好是此最大方向导数。

2.2前向传播和反向传播

前向传播就是前向调用，正常的函数调用链而已，没什么特别的，破概念搞得神神秘秘的

比如

def a(input):
    return y

def b(input):
    return y2
# 前向传播
def forward(input):
    y = a(input)
    y2 = b(y)

反向传播

反向传播就是根据误差和学习率，将参数权重进行调整，具体的算法下次会专门写一篇文章进行解析。

3、数据预处理手段

3.1 归一化  (normalization)

将数据放缩到0~1区间，利用公式（x-min）/（max-min）

3.2 标准化（Standardization）

数据的标准化是将数据按比例缩放，使之落入一个小的特定区间。将数据转化为标准的正态分布，均值为0，方差为1

3.3 正则化

正则化的主要作用是防止过拟合，对模型添加正则化项可以限制模型的复杂度，使得模型在复杂度和性能达到平衡。

3.4 独热码编码（one hot）

one hot编码是将类别变量转换为机器学习算法易于使用的一种形式的过程。one-hot通常用于特征的转换

比如：一周七天，第三天可以编码为 [0,0,1,0,0,00]

注：我把英语都补在了后面，并不是为了装逼，只是为了下次看到这个单词的时候知道这个单词在表示什么。

4、数据处理库

numpy ，pandas， matplotlib 这三个是数据分析常用的库，也是深度学习中常用的三个库

4.1 numpy

numpy 是优化版的python的列表，提高了运行效率，也提供了很多便利的函数，一般在使用的时候表示矩阵

numpy中的一个重要概念叫shape ,也就是表示维度

注：numpy 的api 我也使用不熟练，相信会在以后的学习过程中熟练的，使用的时候查一查，不用担心。

4.2 pandas

Pandas 的主要数据结构是 Series （一维数据）与 DataFrame（二维数据）.

[Series] 是一种类似于一维数组的对象，它由一组数据（各种Numpy数据类型）以及一组与之相关的数据标签（即索引）组成。

DataFrame 是一个表格型的数据结构，它含有一组有序的列，每列可以是不同的值类型（数值、字符串、布尔型值）。DataFrame 既有行索引也有列索引，它可以被看做由 Series 组成的字典（共同用一个索引）。

注：pandas 可以当做Excel使用，里面的api 我也使用不熟练，不用担心，可以扫下核心概念就好

4.3 matplotlib

Matplotlib 是画图用的，可以用来在学习的过程中对数据进行可视化，我还没有学习这个库，只会照猫画虎，所以放轻松，只是告诉你有这么个东西，不一定现在就要掌握

5、训练集、测试集，测试集

训练集：用来训练模型的数据，用来学习的

验证集：用来验证模型的数据，主要是看下模型的训练情况

测试集: 训练完成之后，验证模型的数据

一般数据的比例为6:2:2

一个形象的比喻：

训练集----学生的课本；学生 根据课本里的内容来掌握知识。

验证集----作业，通过作业可以知道 不同学生学习情况、进步的速度快慢。

测试集----考试，考的题是平常都没有见过，考察学生举一反三的能力。

6、损失函数

损失函数用来评价模型的预测值和真实值不一样的程度，损失函数越好，通常模型的性能越好。不同的模型用的损失函数一般也不一样.

注：f(x) 表示预测值，Y 表示真实值，

这些只是常用的损失函数，实现不同而已，在后面的开发理解各个函数就行了，API caller 不用理解具体的实现，就像你知道快速排序的算法原理，但是没必要自己去实现，现成的实现拿来用不香吗？

7、优化器

优化器就是在深度学习反向传播过程中，指引损失函数（目标函数）的各个参数往正确的方向更新合适的大小，使得更新后的各个参数让损失函数（目标函数）值不断逼近全局最小。

常见的几种优化器

8、激活函数

激活函数就是对输入进行过滤，可以理解为一个过滤器

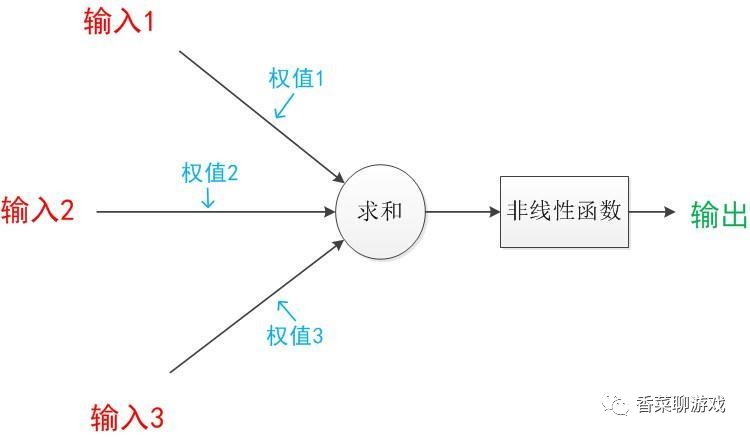
常见的非线性激活函数通常可以分为两类，一种是输入单个变量输出单个变量，如sigmoid函数，Relu函数；还有一种是输入多个变量输出多个变量，如Softmax函数，Maxout函数。

• 对于二分类问题，在输出层可以选择 sigmoid 函数。
• 对于多分类问题，在输出层可以选择 softmax 函数。
• 由于梯度消失问题，尽量sigmoid函数和tanh的使用。
• tanh函数由于以0为中心，通常性能会比sigmoid函数好。
• ReLU函数是一个通用的函数，一般在隐藏层都可以考虑使用。
• 有时候要适当对现有的激活函数稍作修改，以及考虑使用新发现的激活函数。

9、hello world

说了很多概念，搞个demo 看看，下面是一个最简单的线性回归的模型。

环境的安装在文章的开头。

import torch as t
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
import numpy as np

# 学习率，也就是每次参数的移动的大小
lr = 0.01
# 训练数据集的次数
num_epochs = 100
# 输入参数的个数
in_size = 1
#输出参数的个数
out_size = 1
# x 数据集
x_train = np.array([[3.3], [4.4], [5.5], [6.71], [6.93], [4.168],
                    [9.779], [6.182], [7.59], [2.167], [7.042],
                    [10.791], [5.313], [7.997], [3.1]], dtype=np.float32)
# y 对应的真实值
y_train = np.array([[1.7], [2.76], [2.09], [3.19], [1.694], [1.573],
                    [3.366], [2.596], [2.53], [1.221], [2.827],
                    [3.465], [1.65], [2.904], [1.3]], dtype=np.float32)
# 线性回归网络
class LinerRegression(nn.Module):
    def __init__(self, in_size, out_size):
        super(LinerRegression, self).__init__()
        self.fc1 = nn.Linear(in_size, out_size)

    def forward(self, x):
        y_hat = self.fc1(x)
        return y_hat

model = LinerRegression(in_size, out_size)
# 损失函数
lossFunc = nn.MSELoss()
# 优化器
optimizer = optim.SGD(model.parameters(), lr=lr)
# 对数据集训练的循环次数
for epoch in range(num_epochs):
    x = t.from_numpy(x_train)
    y = t.from_numpy(y_train)
    y_hat = model(x)
    loss = lossFunc(y_hat, y)
    # 导数归零
    optimizer.zero_grad()
    # 反向传播，也就是修正参数，将参数往正确的方向修改
    loss.backward()
    optimizer.step()
    print("[{}/{}] loss:{:.4f}".format(epoch+1, num_epochs, loss))

# 画图看下最终的模型拟合的怎么样
y_pred = model(t.from_numpy(x_train)).detach().numpy()
plt.plot(x_train, y_train, 'ro', label='Original Data')
plt.plot(x_train, y_pred, 'b-', label='Fitted Line')
plt.legend()
plt.show()

上面是最简单的一个线性回归的神经网络，没有隐藏层，没有激活函数。

运行很快，因为参数很少,运行的最终结果可以看下，最终达到了我们的结果，你可以试着调整一些参数

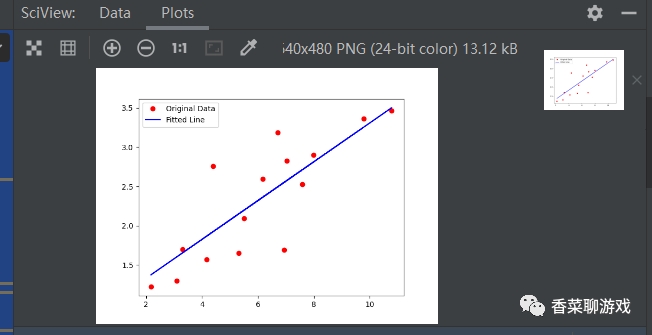
10、总结

今天写了很多的概念，不需要全部掌握，先混个脸熟，先有个全局观，慢慢的认识即可，里面的公式很多，不需要看懂，be easy.

到此这篇关于pytorch之深度神经网络概念全面整理的文章就介绍到这了,更多相关pytorch神经网络内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！