IIS8中添加WCF支持几种方法小结[图文]

方法一

最近在做Silverlight，Windows Phone应用移植到Windows 8平台，在IIS8中测试一些传统WCF服务应用，发现IIS8不支持WCF服务svc请求，后来发现IIS8缺少对WCF服务的Managed Handler，按照以下步骤添加后，IIS8即支持WCF服务。

1. 首先添加MIME类型 扩展名“.svc”，MIME类型 “application/octet-stream”

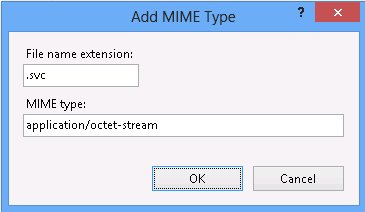
2. 然后在“Handler Mappings”中添加Managed Handler，

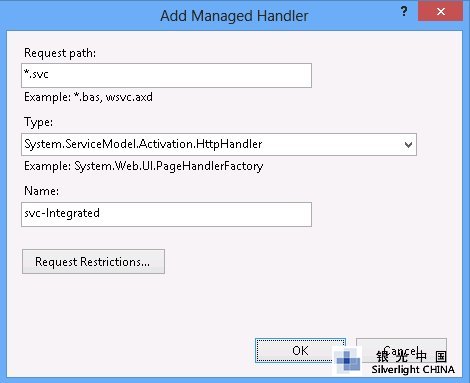
Request path: *.svc
Type: System.ServiceModel.Activation.HttpHandler
Name: svc-Integrated

方法二

另外一种解决方法。

图-1

图-2

解决方法：

只需在“启用或关闭Windows功能”添加如下功能(红线标注):

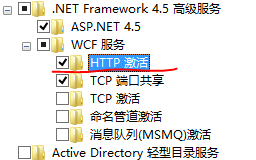
之后，会看到在IIS的 “处理程序映射”中就会有：

好了，“在IIS8中添加WCF服务支持”的问题就迎刃而解

赞 (0)

相关推荐

  • 让IIS8支持WCF的更简单方法

    让IIS8支持WCF的更简单方法

    以前在IIS8中使用WCF时,总是参考在IIS8服务器添加WCF服务支持的方法进行手工设置: 复制代码 代码如下: 1. 首先添加MIME类型:扩展名".svc",MIME类型 "application/octet-stream": 2. 然后在"Handler Mappings"中添加Managed Handler:Request path: *.svcType: System.ServiceModel.Activation.HttpHandl

  • 在IIS8服务器添加WCF服务支持的方法

    在IIS8服务器添加WCF服务支持的方法

     最近在做Silverlight,Windows Phone应用移植到Windows 8平台,在IIS8中测试一些传统WCF服务应用,发现IIS8不支持WCF服务svc请求,后来发现IIS8缺少对WCF服务的Managed Handler,按照以下步骤添加后,IIS8即支持WCF服务. 1. 首先添加MIME类型 扩展名".svc",MIME类型 "application/octet-stream"  2. 然后在"Handler Mappings&quo

  • IIS8中添加WCF支持几种方法小结[图文]

    IIS8中添加WCF支持几种方法小结[图文]

    方法一 最近在做Silverlight,Windows Phone应用移植到Windows 8平台,在IIS8中测试一些传统WCF服务应用,发现IIS8不支持WCF服务svc请求,后来发现IIS8缺少对WCF服务的Managed Handler,按照以下步骤添加后,IIS8即支持WCF服务. 1. 首先添加MIME类型 扩展名".svc",MIME类型 "application/octet-stream" 2. 然后在"Handler Mappings&q

  • Java 在PDF中添加条形码的两种方法

    条形码,是由宽度不等的多个黑条和空白所组成,用以表达一组信息的图形标识符.通过给文档添加条形码,可以直观,快捷地访问和分享一些重要的信息.本文就将通过使用Java程序来演示如何在PDF文档中添加Codebar.Code128A和Code39条形码.除此之外,还可支持创建Code11.Code128B.Code32.Code39 Extended .Code93和Code93 Extended条形码. 使用工具:Free Spire.PDF for Java(免费版) Jar文件获取及导入: 方法

  • Java中List分片的5种方法小结

    Java中List分片的5种方法小结

    目录 简介 1.Google Guava 2.apache commons 3.Hutool 4.JDK 5.自定义分片 总结 前些天在实现 MyBatis 批量插入时遇到了一个问题,当批量插入的数据量比较大时,会导致程序执行报错,如下图所示: 原因是 MySQL 只能执行一定长度的 SQL 语句,但当插入的数据量较多时,会生成一条很长的 SQL,这样程序在执行时就会报错. 要解决这个问题,有两种方法:第一,设置 MySQL 可以执行 SQL 的最大长度:第二,将一个大 List 分成 N 个小

  • 关于C++中定义比较函数的三种方法小结

    C++编程优与Pascal的原因之一是C++中存在STL(标准模板库).STL存在很多有用的方法. C++模板库中的许多方法都需要相关参数有序,例如Sort().显然,如果你想对一个集合进行排序,你必须要知道集合中的对象,那个在前那个在后.因此,学会如何定义比较方法是非常重要的. C++模板库的许多容器需要相关类型有序,例如set<T> 和priority_queue<T>. 这篇文章旨在告诉大家如何为一个类定义一个排序方法,以便在STL容器或者方法中使用. 作为一个C++程序员,

  • python 字典中取值的两种方法小结

    如下所示: a={'name':'tony','sex':'male'} 获得name的值的方式有两种 print a['name'],type(a['name']) print a.get('name'),type(a.get('name')) 发现这两个结果完全一致,并没有任何的差异. 怎么选择这两个不同的字典取值方式呢? 如果字典已知,我们可以任选一个,而当我们不确定字典中是否存在某个键时,我之前的做法如下 if 'age' in a.keys(): print a['age'] 因为不先

  • Python中取整的几种方法小结

    前言 对每位程序员来说,在编程过程中数据处理是不可避免的,很多时候都需要根据需求把获取到的数据进行处理,取整则是最基本的数据处理.取整的方式则包括向下取整.四舍五入.向上取整等等.下面就来看看在Python中取整的几种方法吧. 1.向下取整 向下取整直接用内建的 int() 函数即可: >>> a = 3.75 >>> int(a) 3 2.四舍五入 对数字进行四舍五入用 round() 函数: >>> round(3.25); round(4.85)

  • MySQL表中添加时间戳的几种方法

    MySQL表中添加时间戳的几种方法

    场景: 有张表的数据需要用同步工具同步至其他库,需要 update_time 时间戳字段 来做增量同步. 解决方法: alter table quant_stk_calc_d_wxcp add update_time timestamp DEFAULT CURRENT_TIMESTAMP ON UPDATE CURRENT_TIMESTAMP; 以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持我们.

  • 在vue中使用 jquery 的两种方法小结

    目录 vue中使用 jquery的方法 方法一 方法二 vue和jquery混用注意事项 vue+jquery应该如何使用呢? vm实例里面如何调用外部的jq方法呢? vue中使用 jquery的方法 方法一 直接在vue项目的index.html中引入 外部链接即可 #index.html文件中 <script src="https://cdn.bootcdn.net/ajax/libs/jquery/3.5.1/jquery.js"></script> 不推

  • 基于Android在布局中动态添加view的两种方法(总结)

    一.说明 添加视图文件的时候有两种方式:1.通过在xml文件定义layout:2.java代码编写 二.前言说明 1.构造xml文件 2.LayoutInflater 提到addview,首先要了解一下LayoutInflater类.这个类最主要的功能就是实现将xml表述的layout转化为View的功能.为了便于理解,我们可以将它与findViewById()作一比较,二者都是实例化某一对象,不同的是findViewById()是找xml布局文件下的具体widget控件实例化,而LayoutI

  • Python在图片中添加文字的两种方法

    Python在图片中添加文字的两种方法

    本文主要介绍的是利用Python在图片中添加文字的两种方法,下面分享处理供大家参考学习,下来要看看吧 一.使用OpenCV 在图片中添加文字看上去很简单,但是如果是利用OpenCV来做却很麻烦.OpenCV中并没有使用自定义字体文件的函数,这不仅意味着我们不能使用自己的字体,而且意味着他无法显示中文字符.这还是非常要命的事情.而且他显示出来的文字位置也不太好控制.比如下面的代码,他想做的仅仅是显示数字3: 代码: #coding=utf-8 import cv2 import numpy as

随机推荐