c++实现高精度加法

最近遇到一个c++实现高精度加法的问题，高精度问题往往十复杂但发现其中的规律后发现并没有那么复杂，这里我实现了一个整数的高精度加法，主要需要注意以下几点：

1：将所需输入的数据以字符数组的形式输入，建立字符数组，建立相应的整数数组，然后一一映射，以此来实现数据的输入，需要注意的是，当实现字符向数字映射时，应该减去相应的ASCII偏移值，即48。

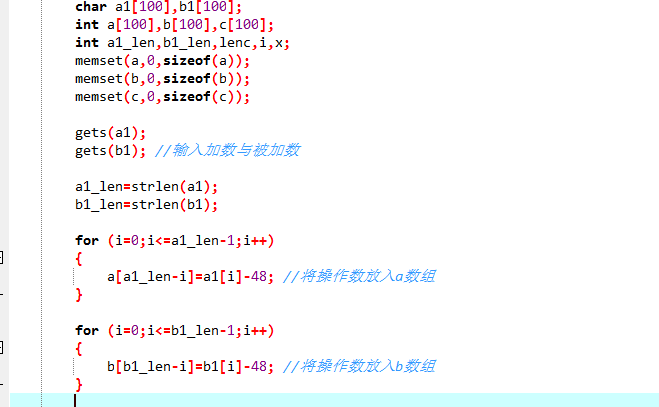
2：为了模拟我们在纸上手算的进位模拟运算，我们将字符数组反向填入整数数组，上图的后几行代码实现了这个操作。

3：实现进位加法，这是整个代码的核心部分，需要读者细细体会，认真揣摩，往往需要反复思考，容易遗忘

4：反向输出数据。因为我们的加法是将数组反置，然后由左到右想加的，加完后，个数位在左边，所以，需要反向输出

以下是全部代码：

  #include<iostream>
  #include<cstdio>
  #include<cstring>
  using namespace std;
  int main()
  {
    char a1[100],b1[100];
    int a[100],b[100],c[100];
    int a1_len,b1_len,lenc,i,x;
    memset(a,0,sizeof(a));
    memset(b,0,sizeof(b));
    memset(c,0,sizeof(c)); 

    gets(a1);
    gets(b1); //输入加数与被加数  

    a1_len=strlen(a1);
    b1_len=strlen(b1);  

    for (i=0;i<=a1_len-1;i++)
    {
      a[a1_len-i]=a1[i]-48; //将操作数放入a数组 　
    } 

    for (i=0;i<=b1_len-1;i++)
    {
      b[b1_len-i]=b1[i]-48; //将操作数放入b数组
    }  

    lenc =1;
    x=0;  

    while(lenc <=a1_len || lenc <=b1_len)
    {
      c[lenc]=a[lenc]+b[lenc]+x; //两数相加 　
      x=c[lenc]/10;  //要进的位
      c[lenc]=c[lenc]%10;   //进位后的数
      lenc++;   //数组下标加1
    } 

    c[lenc]=x;
    if (c[lenc]==0)
    {
      lenc--; //处理最高进位
    }  

    for (i=lenc;i>=1;i--)
    {
      cout<<c[i]; //输出结果
    }
    cout<<endl; 

    return 0;
  }

以上就是本文给大家分享的代码了，希望大家能够喜欢

赞 (0)

相关推荐

  • 深入C/C++浮点数在内存中的存储方式详解

    任何数据在内存中都是以二进制的形式存储的,例如一个short型数据1156,其二进制表示形式为00000100 10000100.则在Intel CPU架构的系统中,存放方式为  10000100(低地址单元) 00000100(高地址单元),因为Intel CPU的架构是小端模式.但是对于浮点数在内存是如何存储的?目前所有的C/C++编译器都是采用IEEE所制定的标准浮点格式,即二进制科学表示法.在二进制科学表示法中,S=M*2^N 主要由三部分构成:符号位+阶码(N)+尾数(M).对于flo

  • 基于C++浮点数(float、double)类型数据比较与转换的详解

    浮点数在内存中的存储机制和整型数不同,其有舍入误差,在计算机中用近似表示任意某个实数.具体的说,这个实数由一个整数或定点数(即尾数)乘以某个基数(计算机中通常是2)的整数次幂得到,这种表示方法类似于基数为10的科学记数法.所以浮点数在运算过程中通常伴随着因为无法精确表示而进行的近似或舍入.但是这种设计的好处是可以在固定的长度上存储更大范围的数.1.将字符串转换为float.double过程存在精度损失,只是float.double各自损失的精度不相同而已std::string str="8.2&

  • 解析C++浮点数无效值的定义与无效值判定的小结

    在实际计算中可能会出现浮点型的无效数据,格式化输出到文件中内容为1.79769e+308,输出到界面就是很大一串数据.这两种方式无论哪种在阅读和查找时就不是很方便.在开发中遇见浮点型数据无效值得判定. 无效值定义如下:#define InvalidDouble *(double*)("\xff\xff\xff\xff\xff\xff\xef\x7f")double  price;.........(计算步骤省掉)price=GetPrice(); //获取数据 通过下面方式对浮点型的无

  • 解析C++ 浮点数的格式化显示

    代码如下所示: 复制代码 代码如下: #include <stdlib.h>      #include <string>      #include <windows.h>      #include <stdio.h>      #include <iostream>      #include <limits>      #include <sstream>      using namespace std; str

  • C++数据精度问题的解决方案(对浮点数保存指定位小数)

     1.背景 对浮点数保存指定位小数.比如,  1.123456.   要保存1位小数,,调用方法后, 保存的结果为: 1.1. 再比如,1.98765,  保存2位小数的结果为: 2.00. 2. 解决方案 A.添加头文件 #include <sstream> #include <iomanip> B.添加命名空间 using namespace std; C.添加函数 /*******************************************************

  • c++加法高精度算法的简单实现

    c++高精度算法,对于新手来说还是一大挑战,只要克服它,你就开启了编程的新篇章,算法. 我发的这个代码并不是很好,占用内存很多而且运行时间很长(不超过1秒),但是很好理解,很适合新手 高精算法的本质就是把数组编程字符串,然后将字符串像竖式一样加起来: a+b高精度算法 #include <iostream> #include <cmath> #include <cstring> using namespace std; int main() { char a[10001

  • 使用C++的string实现高精度加法运算的实例代码

    对于超大数字的运算,用long long int仍然不能解决,这时候就需要考虑通过模拟运算和数组存储来实现高精度运算. 本文讨论借助C++的string来实现高精度的运算. 首先输入的量直接存储为string,设为s1和s2. 接下来设计一个反转函数,用于把整个字符串反转(为了方便后续计算). string reverseStr(string input){ string output = ""; for(int i = 0; i < input.length(); i++){

  • c++实现高精度加法

    c++实现高精度加法

    最近遇到一个c++实现高精度加法的问题,高精度问题往往十复杂但发现其中的规律后发现并没有那么复杂,这里我实现了一个整数的高精度加法,主要需要注意以下几点: 1:将所需输入的数据以字符数组的形式输入,建立字符数组,建立相应的整数数组,然后一一映射,以此来实现数据的输入,需要注意的是,当实现字符向数字映射时,应该减去相应的ASCII偏移值,即48. 2:为了模拟我们在纸上手算的进位模拟运算,我们将字符数组反向填入整数数组,上图的后几行代码实现了这个操作. 3:实现进位加法,这是整个代码的核心部分,需

  • C语言实现高精度加法

    C语言实现高精度加法

    本篇为高精度加法的计算,接下来我还会去写高精度乘法的计算. 一.高精度运算的概念 高精度运算其实就是参与运算的数完全超出基本数据类型所能表示的范围的运算(例如int型范围就是 - 2147483648 ~+ 2147483647) 所以如果想求较大数的话就要创建新的数据类型 二.数据类型的选取 我选择的是int型数组,这样比较便于计算和理解 三.代码 其中a和b我是通过随机数来赋值 //author summer_awn //date 2017/6/20 #include<iostream>

  • 大数(高精度数)模板(分享)

    复制代码 代码如下: #include <stdio.h>#include <string.h> #include <stdlib.h> #include <math.h>#include <assert.h>  #include <ctype.h> #include <map>#include <string>#include <set>#include <bitset>#includ

  • C/C++高精度算法的实现

    做ACM题的时候,经常遇到大数的加减乘除,乘幂,阶乘的计算,这时给定的数据类型往往不够表示最后结果,这时就需要用到高精度算法.高精度算法的本质是把大数拆成若干固定长度的块,然后对每一块进行相应的运算.这里以考虑4位数字为一块为例,且输入的大数均为正整数(也可以考虑其他位,但要注意在每一块进行相应运算时不能超出数据类型的数值范围:有负整数的话读入时判断一下正负号在决定运算). 1. 高精度加法 以3479957928375817 + 897259321544245为例: 3479 9579 283

  • C语言实现高精度加减法

    本文实例为大家分享了C语言实现高精度加减法的具体代码,供大家参考,具体内容如下 首先,我们来看一下C语言中各类型的最值: unsigned int 0-4294967295 int -2147483648-2147483647 unsigned long 0-4294967295 long -2147483648-2147483647 long long的最大值:9223372036854775807 long long的最小值:-9223372036854775808 unsigned lon

  • C/C++高精度运算(大整数运算)详细讲解

    目录 前言 什么是大整数 大整数的表示 大整数的运算 1.高精度加法 2.高精度减法 3.高精度乘以低精度 4.高精度除以低精度 大整数的表示 补充:使用示例 总结 前言 高精度的运算在算法题尤为常见,在处理一些大型数据的项目中也需要用到.虽然Boost库中有处理高精度问题的模板,但是标准库中并没有.为了方便学习,本文提供了高精度运算的模板,供大家参考. 什么是大整数 众所周知,最大的整型long long的范围是[-9223372036854775808~9223372036854775807

  • C++高精度算法的使用场景详解

    目录 描述 1. 高精度加法 1. 思路 2. 代码 2. 高精度减法 1. 思路 2. 代码 3. 如果出现被减数的位数小于减数时呢 描述 如果要计算的数超过了long long怎么解决? —>使用高精度加减乘除,简单理解就是 很大的数进行加减乘除. 1. 高精度加法 1. 思路 创建对应的数组变量及其他变量 输入字符串 将读入的数据转化为整数类型,并逆序(反转)存储到数组中 将两个数组做累加(注意进位) 判断最高位是否为0,大于0代表进位了,则让长度加1 倒序输出 2. 代码 #includ

  • C C++ 算法实例大全

    C C++,算法实例 一.数论算法   1．求两数的最大公约数 function gcd(a,b:integer):integer; begin if b=0 then gcd:=a else gcd:=gcd (b,a mod b); end ; 2．求两数的最小公倍数 function lcm(a,b:integer):integer; begin if a<b then swap(a,b); lcm:=a; while lcm mod b>0 do inc(lcm,a); end; 3．

随机推荐