Python之维度dim的定义及其理解使用方式

目录

• 一、dim的定义
• 二、dim 的理解
• 三、举例
• torch.argmax()
• sum()
• cumsum()
• 总结

一、dim的定义

TensorFlow对张量的阶、维度、形状有着明确的定义，而在pytorh中对其的定义却模糊不清，仅仅有一个torch.size()的函数来查看张量的大小（我理解的这个大小指的就是TensorFlow对张量的形状描述，也和numpy的.shape类似）。

所以，首先要搞清楚如何看一个张量的形状。

import torch
z = torch.ones(2,3,4)
print(z)
print(z.size())
print(z.size(0))
print(z.size(1))
print(z.size(2))

以上代码的控制台输出为：

tensor([[[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]],
 
        [[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]]])
torch.Size([2, 3, 4])
2
3
4

可见，我们成功创建了一个（2，3，4）大小的张量，那么我们人工应该怎么辨别一个张量的大小呢？

为了直观，我把这个张量的中括号调整一个位置：

[
    [
         [1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]
    ],
 
    [
         [1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]
    ]
]

我们可以看到：

• 第一层（最外层）中括号里面包含了两个中括号（以逗号进行分割），这就是（2，3，4）中的2
• 第二层中括号里面包含了三个中括号（以逗号进行分割），这就是（2，3，4）中的3
• 第三层中括号里面包含了四个数（以逗号进行分割），这就是（2，3，4）中的4

结论：pytorch中的tensor维度可以通过第一个数前面的中括号数量来判断，有几个中括号维度就是多少。拿到一个维度很高的向量，将最外层的中括号去掉，数最外层逗号的个数，逗号个数加一就是最高维度的维数，如此循环，直到全部解析完毕。

我们还看到：

z.size(0) = 2，z.size(1) = 3，z.size(2) = 4

第0维度为2，第1维度为3，第2维度为4，即维度的标号是以0开始的

二、dim 的理解

网上很多对dim的理解，比如，dim=0，表示的是行，函数的意思就是不要行这一维度，保留列巴拉巴拉之类的，个人觉得不好理解。

比如下图博主的理解

那我的理解就是：

控制变量法大家知道吗？？或者消融实验？就是几个方法或者实验的比较，保持只有一个因素是可变的，其他都是一致的，就是控制变量法，论文术语也叫消融实验。

所以，dim的使用也是这样，只有dim指定的维度是可变的，其他都是固定不变的。

• dim = 0，列不变（按列-将当前列所有行数据-计算），指定的是行，那就是行变，理解成：针对每一列中，所有行之间的数据比较或者求和等操作，是每一行的比较，因为行是可变的。
• dim = 1，行不变（按行-将当前行所有列数据-计算），指定的是列，那就是列变，理解成：针对每一行中，所有列之间的数据比较或者求和等操作，是每一行的比较，因为行是可变的。

三、举例

torch.argmax()

• 得到最大值的序号索引
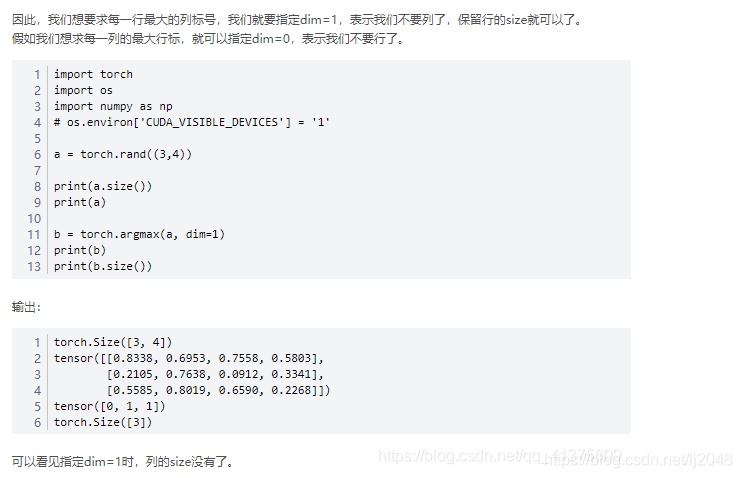
• dim=0保留列维度，不要行了，保留列的size就可以了
• dim=1保留行维度，不要列了，保留行的size就可以了

a = torch.rand((3,4))
print(a)
b = torch.argmax(a, dim=1) ##行不变，指定列，列之间的比较，对下面每列数值进行比较，将最大值对应序号存下，比如下面第一列中第一个值最大，为0，第二列中第二个是最大值，为1，第三列同
print(b)
>>tensor([[0.8338, 0.6953, 0.7558, 0.5803],
        [0.2105, 0.7638, 0.0912, 0.3341],
        [0.5585, 0.8019, 0.6590, 0.2268]])
>>tensor([0, 1, 1])

说明：dim=1，指定列，也就是行不变，列之间的比较，所以原来的a有三行，最后argmax()出来的应该也是三个值，第一行的时候，同一列之间比较，最大值是0.8338，索引是0，同理，第二行，最大值的索引是1……

sum()

求和

a = t.arange(0,6).view(2,3)
a
>>tensor([[0, 1, 2],
        [3, 4, 5]])
a.sum()
a.sum(dim=0) #列不变，指定行，行是可变的，对每一列中的所有行之间的数值进行求和，比如这个例子中，第一列0+3，第二列1+4，第三列2+5
a.sum(dim=1) #行不变，指定列，列是可变的，对每一行中的所有列之间的数值进行求和，比如这个例子中，第一行0+1+2，第二行3+4+5
>>tensor(15.)
>>tensor([3., 5., 7.])
>>tensor([ 3., 12.])

说明：dim=0，指定行，行是可变的，列是不变，所以就是同一列中，每一个行的比较，所以a.sum(dim = 0)，第一列的和就是3，第二列的和就是5，第三列的和就是7.

同理，a.sum(dim=1)，指定列，列是可变的，行是不变的，所以就是同一列之间的比较或者操作，所以第一行的求和是3，第二行的求和是12

cumsum()

累加

a = t.arange(0,6).view(2,3)
a
>>tensor([[0, 1, 2],
        [3, 4, 5]])
a.cumsum(dim=0)  # 指定行，列不变，行变，从第一行到最后一行的累加
>>tensor([[0, 1, 2],
        [3, 5, 7]])

a.cumsum(dim=1) # 指定列，行不变，列变，从第一列到最后一列的累加
>>tensor([[ 0,  1,  3],
        [ 3,  7, 12]])

总结

以上为个人经验，希望能给大家一个参考，也希望大家多多支持我们。