Java深入浅出理解快速排序以及优化方式

可能经常看面经的同学都知道，面试所遇到的排序算法，快速排序占主要位置，热度只增不减啊，其次就是归并和堆排序。

其实以前写过一篇排序的文章，写的比较简单，只是轻描淡写。今天我再次重新拿起笔，将快速排序的几大优化，再次一一讲述一遍。各位同学，读完这篇文章，如若对你能够带来一些感悟，记得给个大大的赞哦！！！

前言

快速排序是在冒泡排序的基础之上，再次进行优化得来的。具体的步骤如下：

• 在待排序的序列中，选取一个数值，将大于它的数放到数组的右边，小于它的数放到数组的左边，等于它的数就放到数组的中间。
• 此时，相对于上一步挑选出来的数值而言，此时数组的左部分都小于它，右部分都大于它。达到“相对有序”。
• 然后，递归左部分和右部分，重复以上操作即可。

流程知道后，问题就在于如何选取这个基准值？我们有以下几种选取基准值和优化的方法：

• 挖坑法
• 随机取值法
• 三数取中法
• 荷兰国旗问题优化

以上四种，笔试最容易考到的代码题就是挖坑法，可能最难理解的就是荷兰国旗问题带来的优化。要想拿到一个好的offer，以上必须全部掌握，并且还得学会写非递归版本的代码（非递归比较简单）。

本期文章源码：GitHub

以下所有讲解，可能会频繁用到如下交换数值的方法，这里提前写了：

public void swap(int[] array, int L, int R) {
    int tmp = array[L];
    array[L] = array[R];
    array[R] = tmp;
}

一、挖坑法

挖坑法：默认将数组的第一个数值作为基准值。然后做以下步骤：

• 第一、从数组的最后开始遍历（下标R），找到第一个小于基准值的数值。然后将小于的这个数值放入上次空出来的位置（第一次就是基准值的位置）
• 第二、上一步将小于的数值交换位置后，空出来的位置用于：在数组的前面找到第一个大于基准值的数值（下标L），放到这个空出来的位置。
• 循环以上两个步骤，直到遍历到L==R时，循环停止

看如下长图：

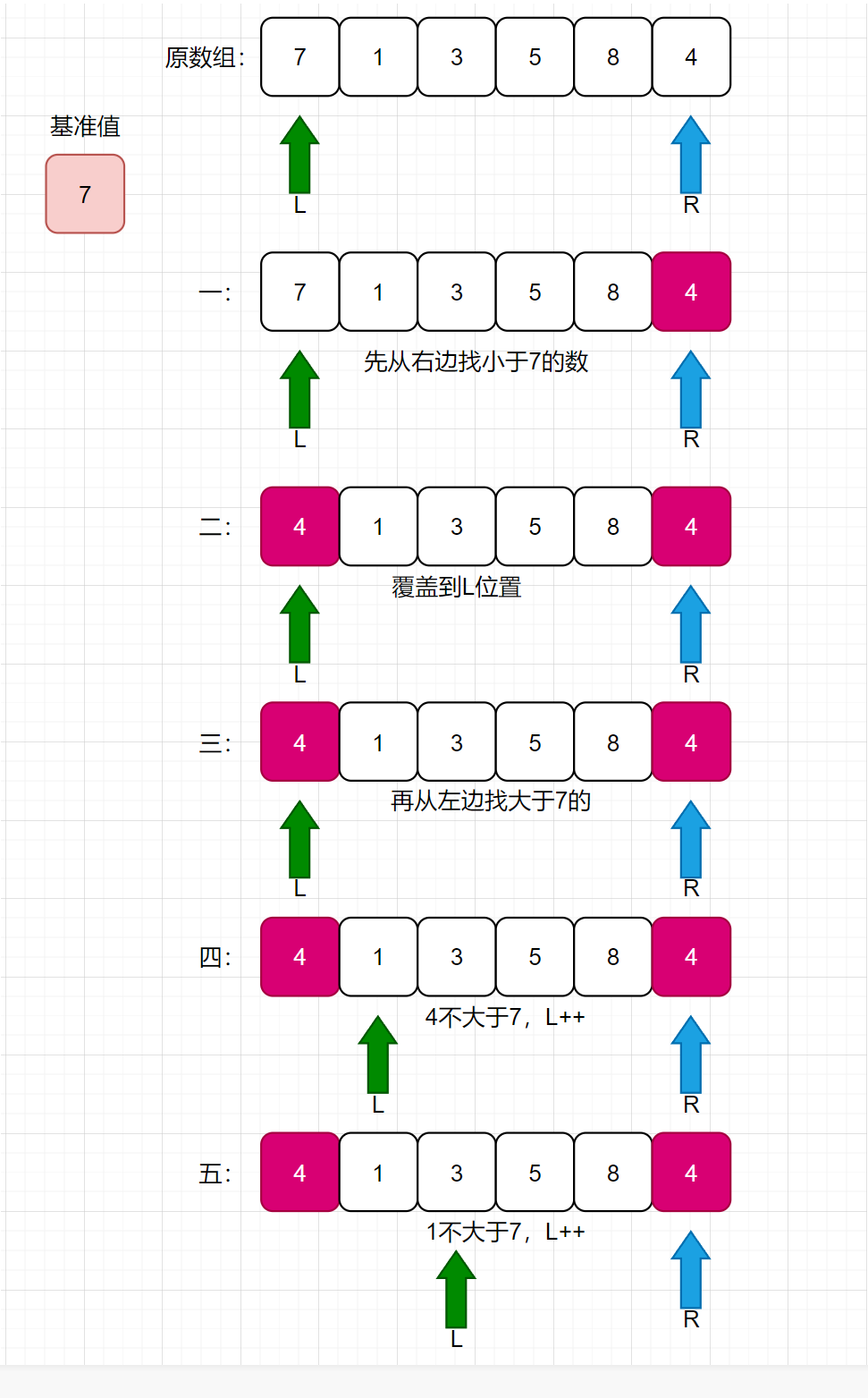
挖坑法，就类似于，我先拿出基准值，此时基准值的位置就空出来了，需要从后面的数值拿一个数来补这个空位置；补完之后，后面的位置又空出来了，此时再从前面的数组找一个数去补后面的空位置，循环往复，知道L和R相遇。再把基准值放入此时的L位置即可。

此时，整个数组，就从基准值位置分为了两部分，分别递归左部分和右部分即可。

//挖坑法-升序
public int partition(int[] array, int L, int R) {
    int tmp = array[L]; //保存基准值
    while (L < R) {
        //先从右边找一个数
        while (L < R && array[R] >= tmp) {
            R--; //找小于基准值的数
        }
        array[L] = array[R];

        //再从左边找一个数
        while (L < R && array[L] <= tmp) {
            L++; //找大于基准值的数
        }
        array[R] = array[L];
    }
    array[L] = tmp; //将基准值放入中间位置
    return L; //返回此时基准值的下标，用于将数组分为两部分
}

特别值得注意的是，在数组左右两边查找一个数的时候，while循环的判断（L<R && array[R] <= tmp）; 此时的等于号，切记不能少了，因为当待排序数组中有相同的数据时，会导致死循环。

主方法调用如下：

public void quick(int[] array, int L, int R) {
    if (L >= R) {
        return;
    }
    int p = partition(array, L, R); //返回基准值的下标
    quick(array, L, p - 1); //递归左半部分
    quick(array, p + 1, R); //递归右半部分
}

二、随机取值法

随机取值法：就是在数组范围内，随机抽取一个数值，作为基准值，这里与挖坑法不同的是：挖坑法每次固定以数组的第一个数为基准值，而随机取值法，则是随机的。此时这种优化搭配着挖坑法，有更快的效率。主方法代码如下：

public void quick2(int[] array, int L, int R) {
    if (L >= R) {
        return;
    }
    int index = L + (int)((R - L) * Math.random()); //生成L~R之间的随机值
     //为了好理解，我将这个随机值放到数组开头。也可以不交换，只需改partition即可
    swap(array, L, index);

    int p = partition(array, L, R); //调用挖坑法
    quick2(array, L, p - 1); //递归左半部分
    quick2(array, p + 1, R); //递归右半部分
}

三、三数取中法

三数取中法：原意是，随机生成数组范围内的三个数，然后取三者的中间值作为基准值。但是在后序变化中，就没有随机生成，而是直接以数组的第一个数、最后一个数和中间数，这三个位置的数，取中间值，作为基准值。也是搭配着挖坑法来使用的，与随机取值法一样，都是起到优化的作用。

public void quick3(int[] array, int L, int R) {
    if (L >= R) {
        return;
    }
    threeNumberMid(array, L, R); //三数取中，并将中间值，放到数组最前面
    int p = partition(array, L, R);
    quick3(array, L, p - 1);
    quick3(array, p + 1, R);
}

private void threeNumberMid(int[] array, int L, int R) {
    int mid = L + ((R - L) >> 1); //中间值
    if (array[L] > array[R]) {
        swap(array, L, R);
    }
    if (array[L] > array[mid]) {
        swap(array, L, mid);
    }
    if (array[mid] > array[R]) {
        swap(array, mid, R);
    }
    //以上三个if过后，这三个数就是一个升序
    //然后将中间值，放到数组的最前面
    swap(array, L, mid);
}

四、荷兰国旗问题优化

荷兰国旗问题所带来的优化，有明显是优于挖坑法的。在以后的使用中，可能这种优化可能会多一点。

至于为什么叫荷兰国旗问题所带来的优化。大家去百度查一下这关键字即可，我们这里就不多说了。

原意是：给定一个数组，将这个数组，以某一个基准值，整体分为三个区域（大于区，小于区、等于区）。然后再去递归小于区和大于区的范围。这就是荷兰国旗问题所带来的优化思想，不同于挖坑法的是，这种优化，会将所有等于基准值的数，都聚集在中间，这样的话，分别去递归左右两边的子数组时，范围上就有一定的缩小。

具体步骤：

• 有三个变量（less，more，index）。分别表示小于区的右边界、大于区的左边界，index则表示遍历当前数组的下标值。less左边都是小于基准值的，more右边都是大于基准值的。如下图：暂时先不看more范围内的50，等会说明。

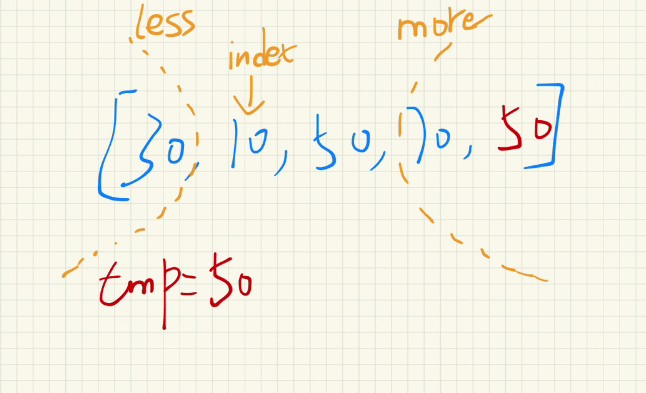
• index从左开始遍历，每遍历一个数，进行判断，小于基准值，就划分到less区域；大于基准值就划分到more区域；等于的话，不交换，index往后走就行。
• 循环上一走即可，直到index和more相遇就停止。

//伪代码
public int[] partition(int[] array, int L, int R) {
    int less = L - 1;
    int more = R;
    int index = L;
    while (index < more) { //index和more相遇就停止
        if (array[index] > 基准值) {

        } else if (array[index] < 基准值) {

        } else { //等于基准值时，index后移即可
            index++;
        }
    }

    //返回等于区的开始和结束下标即可。
}

以上就是荷兰国旗问题的伪代码，是不是感觉很简单？？？返回的是一个数组，这个数组只有两个元素，第一个元素就是等于区的开始下标，第二个元素就是等于区的结束下标。

具体的思想我们讲了，但是还是会遇到一个问题，那就是基准值的选择。我们只需套用前面讲过的随机取值法或者三数取中法即可。

我们前面将随机取值法的时候，是将随机抽取的基准值，放到数组的第一个元素的位置，然后再去调用partition方法，进行挖坑法的。这里我们就换一下，将随机抽取的基准值，放到数组的末尾。这也就是在上一张图中，为什么more范围内的50是红色的原因。因为它就是基准值，只是暂时先放到了数组的最后而已。（当然，也可以像挖坑法一样，放到数组的第一个元素位置，一样的道理，只是partition方法稍微修改一下初始值即可）。

既然我们将基准值放到了数组的末尾，那么在while循环结束后，也就是index遍历完之后，也需要将最后这个基准值放回到等于区的范围。而此时数组状态是这样的：L……less是小于区，less+1 …… more - 1是等于区，more …… R是大于区。

我们将最后这个基准值放到等于区的末尾即可，也就是调用swap(array, more, R)。R是基准值的位置，more是大于区的开始位置。

所以完整的partition代码如下：

//R位置就是基准值
public int[] partition(int[] array, int L, int R) {
    if (L > R) {
        return new int[] {-1, -1};
    }
    if (L == R) {
        return new int[] {L, L};
    }

    int less = L - 1; //数组最前面开始为less
    int more = R; //数组末尾，包括了最后的基准值
    int index = L; //遍历数组
    while (index < more) {
        if(array[index] > array[R]) { //大于区
            swap(array, index, --more);
        } else if (array[index] < array[R]) { //小于区
            swap(array, index++, ++less);
        } else { //等于区
            index++;
        }
    }
    swap(array, more, R); //将最后的基准值放回等于区
    //此时的范围：L …… less 是小于区。less+1 ……more 是等于区。more + 1 …… R是大于区
    return new int[] {less+1, more};
}

特别值得注意的是，循环里第一个if语句，大于基准值的时候，从与数组后面的元素交换。但是从数组后面交换过来的数据，并不知道大小情况，所以此时的index还不能移动，需再次判断交换过来的数据才行。其他的注意地方就是less和more的变化，留意一下是前置++-- 。

主方法的调用：

public void quick(int[] array, int L, int R) {
    if (L >= R) {
        return;
    }
    int i = L + (int)((R - L) * Math.random()); //随机值
    swap(array, i, R); //放到数组的最后
    int[] mid = partition(array, L, R); //返回的是等于区的范围
    quick(array, L, mid[0] - 1); //左半部分
    quick(array, mid[0] + 1, R); //右半部分
}

五、非递归版本

讲完了快速排序的挖坑法和荷兰国旗问题的优化，剩下的就很简单了。非递归的话，就是申请一个栈，栈里压入的是待排序数组的开始下标和结束下标。也就是说，这个入栈时，需要同时压入两个下标值的。弹出的时候，也是同时弹出两个下标值的。

唯一的问题就在于，我该在什么时候进行压入？

• 当此时的右半部分只有一个数据，或者没有数据的时候，此时右半部分就不需要再入栈了。

• 同理，当此时左半部分只有一个数据，或者没有数据的时候，就不需要再入栈了。

以上两点，推导出，当mid[1] + 1 >= R 时，不需要再压入右半部分；当mid[0] - 1 <= L 时，就不需要再压入左半部分。

则可反推：mid[1] + 1 < R时，就压入；mid[0] - 1 > L 时，就压入。则有如下代码：

//非递归版本
public void quick(int[] array) {
    Stack<Integer> stack = new Stack<>();
    stack.push(0);
    stack.push(array.length - 1); 

    while (!stack.isEmpty()) {
        int R = stack.pop();
        int L = stack.pop();
        int[] mid = partition(array, L, R); //调用荷兰国旗问题优化的代码

        if (mid[1] + 1 < R) {
            stack.push(mid[1] + 1);
            stack.push(R);
        }
        if (mid[0] - 1 > L) {
            stack.push(L);
            stack.push(mid[0] - 1);
        }
    }
}

非递归代码，就是需要注意，先压入数组的左边界L，再压入右边界R，则弹出栈的时候，是先弹出R的值。这里需要注意，不要反了。

快速排序的时间复杂度O(NlogN)，空间复杂度O(logN)，没有稳定性。快速排序的时间复杂度，取决于基准值的选择，基准值选在所有数据的中间，将左右部分的子数组平分，就是最优的，能达到O(NlogN)，如果选在所有数据的最小值或最大值，则时间复杂度就会退化为O(N^2)。

还有一个优化就是，当待排序数组的数据个数到达一定的范围时，可直接使用插入排序，会比快速排序快一点点的。

好啦，本期更新就到此结束啦。以上全部就是快速排序的代码，大家需要多敲几遍代码，多过几遍思路，这个排序算法就算收入囊中啦！

我们下期再见吧！！！

到此这篇关于Java深入浅出理解快速排序以及优化方式的文章就介绍到这了,更多相关Java 快速排序内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！