OpenGL画bezier曲线

Bezier Curve算法是根据参数曲线方程来得到光滑曲线的一种算法，曲线方程的参数由控制点决定。
其本质是由调和函数根据控制点插值而成，其参数方程如下：

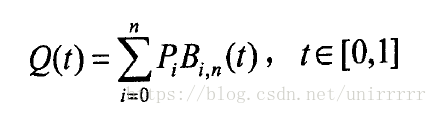
其中Pi（i=0,1，…，n）为控制点的向量，

Bi,n(t)为伯恩斯坦Bernstein基函数，其多项式表示为：

线性Bezier Curve由两个控制点决定：

二次Bezier Curve由三个控制点决定：

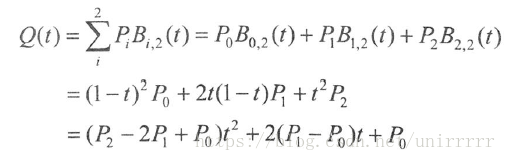
三次Bezier Curve由四个控制点决定：

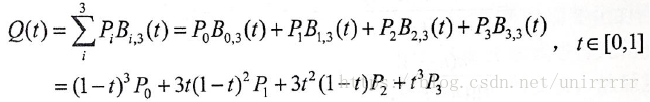
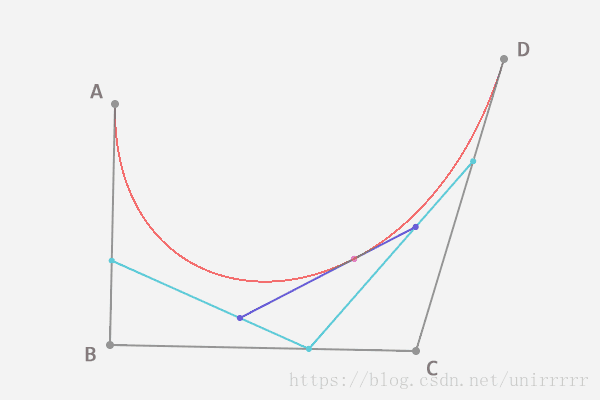
如下图，t = AE:AB = BF:BC = CG:CD = EH:EF = FI:FG = HJ:HI，J即为Bezier曲线上的点

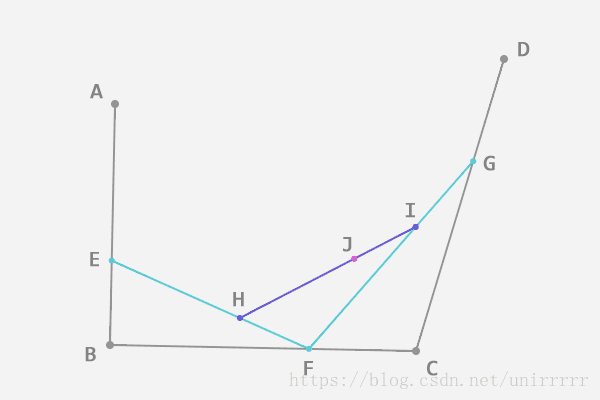
t取0到1的过程就把bezier曲线画出来了。

Bezier Curve的特点：

1、端点性质：通过起点和终点；
2、对称性：保持顶点位置不变，顺序颠倒，新曲线的形状不变，只是参数变化的方向相反；
3、凸包性：由二项式定理得知Bi,n(t)求和为1，即Bi,n(t)构成了Bezier曲线的一组权函数，因此Bezier曲线一定落在其控制多边形的凸包之中。
4、几何不变性：Bezier曲线的形状只与其控制点的相对位置有关，与坐标变化无关。

实现三次Bezier曲线函数的代码如下：vector用于储存构成曲线的点坐标，若每次都重新分配会导致堆溢出，因此每次都用同一内存空间

//用于存储画曲线的点坐标
float* vector = new float[2000];
float* bezierCurve(float step, float* points) {
 //一共有几个点
 int size = 1.0 / step;

 float t = 0.0f;
 //参考公式 Q(t)=(1-t)^3*P0 + 3t(1-t)^2*P1 + 3t^2(1-t)*P2 + t^3*P3
 for (int index = 0; index < size; index++, t += step) {
 vector[index * 3] = (1 - t)*(1 - t)*(1 - t)*points[0] + 3 * t*(1 - t)*(1 - t)*points[3]
    + 3 * t*t*(1 - t)*points[6] + t*t*t*points[9];
 vector[index * 3 + 1] = (1 - t)*(1 - t)*(1 - t)*points[1] + 3 * t*(1 - t)*(1 - t)*points[4]
    + 3 * t*t*(1 - t)*points[7] + t*t*t*points[10];
 vector[index * 3 + 2] = 0.0f;
 }

 return vector;
}

【部分运行效果】

用鼠标左键点击四个点，根据点的顺序画出三次Bezier曲线

改变点的顺序，得到新的Bezier曲线

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。

赞 (0)

相关推荐

  • OpenGL绘制Bezier曲线的方法

    本文实例为大家分享了OpenGL绘制Bezier曲线的具体代码,供大家参考,具体内容如下 项目要求: – 使用鼠标在屏幕中任意设置控制点,并生成曲线 – 使用鼠标和键盘的交互操作实现对曲线的修改. 项目总体介绍 本项目利用Bezier曲线生成算法生成可由用户自定义的曲线.可实现核心功能如下: 1.用户用鼠标左击屏幕任意处产生记录点. 2.鼠标右击屏幕任意处由先前的任意个数记录点和其先后关系生成Bezier曲线. 另有辅助输入功能: 1.按键盘'C'键可清除所有记录点. 2.按键盘'R'键可清除上

  • OpenGL实现Bezier曲线的方法示例

    OpenGL实现Bezier曲线的方法示例

    Bezier曲线的形状是通过一组多边折线(特征多边形)的各顶点唯一地定义出来的.在这组顶点中: (1)只有第一个顶点和最后一个顶点在曲线上: (2)其余的顶点则用于定义曲线的导数.阶次和形状: (3)第一条边和最后一条边则表示了曲线在两端点处的切线方向. // BezierCurve.cpp : 定义控制台应用程序的入口点. // #include "stdafx.h"</div></div></li><li><div class=

  • 基于OpenGL实现多段Bezier曲线拼接

    本文实例为大家分享了OpenGL实现多段Bezier曲线拼接的具体代码,供大家参考,具体内容如下 运行程序的交互方式有点类似corelDraw中的自由曲线绘制,或者photoShop中的钢笔自由路径绘制. 截图: 将BezierCurve封装成了一个类,代码如下: #ifndef _BEZIERCURVE_H #define _BEZIERCURVE_H #include "vec3.hpp" #include <vector> #include <iostream&

  • 使用OpenGL绘制Bezier曲线

    本文实例为大家分享了OpenGL绘制Bezier曲线的具体代码,供大家参考,具体内容如下 最近在看Francis S Hill ,Jr 和 Stephen M Kelley合著的<计算机图形学>(OpenGL版)(第三版)书中有绘制三个控制点的Bezier曲线的代码.自己重新敲了一遍代码.发现了其中的一点小错误,修正过来了.并做了一点小小的改动. 源码见下 #include <windows.h> #include <math.h> #include <gl/GL

  • OpenGL绘制三次Bezier曲线

    本文实例为大家分享了OpenGL绘制三次Bezier曲线的具体代码,供大家参考,具体内容如下 计算公式: 运行结果: 代码如下: #include<gl/glut.h> #include<math.h> #include<windows.h> #include<vector> #include<algorithm> using namespace std; struct Point { int x, y; Point(){}; Point(int

  • OpenGL画bezier曲线

    Bezier Curve算法是根据参数曲线方程来得到光滑曲线的一种算法,曲线方程的参数由控制点决定. 其本质是由调和函数根据控制点插值而成,其参数方程如下: 其中Pi(i=0,1,-,n)为控制点的向量, Bi,n(t)为伯恩斯坦Bernstein基函数,其多项式表示为: 线性Bezier Curve由两个控制点决定: 二次Bezier Curve由三个控制点决定: 三次Bezier Curve由四个控制点决定: 如下图,t = AE:AB = BF:BC = CG:CD = EH:EF = F

  • 解析在Direct2D中画Bezier曲线的实现方法

    解析在Direct2D中画Bezier曲线的实现方法

    Direct2D通过ID2D1RenderTarget接口支持基本图元(直线,矩形,圆角矩形,椭圆等)的绘制,然而,此接口并未提供对曲线绘制的直接支持.因此,想要使用Direct2D绘制一段通过指定点的曲线,比如Bezier曲线,必须借助于DrawGeometry()方法间接实现.需要通过一定的算法,将指定点转换为定义Path的控制点.幸运的是,codproject上已经有人做了这项工作,给出了相应的转换算法,并给出了C#版的实现:Draw a Smooth Curve through a Se

  • 如何通过python画loss曲线的方法

    1. 首先导入一些python画图的包,读取txt文件,假设我现在有两个模型训练结果的records.txt文件 import numpy as np import matplotlib.pyplot as plt import pylab as pl from mpl_toolkits.axes_grid1.inset_locator import inset_axes data1_loss =np.loadtxt("valid_RCSCA_records.txt") data2_l

  • python 画函数曲线示例

    如下所示: import numpy as np import matplotlib.pyplot as plt x = np.linspace(0, 2 * np.pi, 100) y1, y2 = np.sin(x), np.cos(x) plt.plot(x, y1) plt.plot(x, y2) plt.title('line chart') plt.xlabel('x') plt.ylabel('y') plt.show() 以上这篇python 画函数曲线示例就是小编分享给大家的全

  • OpenGL绘制贝塞尔曲线

    本文实例为大家分享了OpenGL绘制贝塞尔曲线的具体代码,供大家参考,具体内容如下 最终效果图: 通过3个点形成一条贝塞尔曲线 1. 鼠标问题 在使用鼠标获取坐标的时候,要知道鼠标获取的坐标和屏幕坐标是不同的; openGL使用右手坐标 从左到右,x递增 从下到上,y递增 从远到近,z递增 而鼠标是从左到右增x,同时从上到下也是增y 所以在求 y 的时候,用(屏幕大小-y)来获取 2. 绘制 setpoint 用来绘制点 setline 用来绘制线 setBezier 用来绘制贝塞尔曲线 其中公

  • OpenGL实现贝塞尔曲线或曲面

    本文实例为大家分享了OpenGL实现贝塞尔曲线或曲面的具体代码,供大家参考,具体内容如下 理论基础 贝塞尔曲线和曲面:OpenGL只能直接绘制基本图元,对于曲线和曲面我们一般采用一系列线段或多边形来模拟的,这样当线段或多边形增多时必定很耗性能.其实对于这种曲线和曲面,我们可以使用一些控制点,通过求值器程序先计算出坐标等信息,然后直接用这些数据绘制,这样不仅节省内存,还提高了模拟曲线或曲面的精度(本质还是通过线段或多边形绘制的,只是求值器提前算出了曲线或曲面的顶点信息). 求值器使用一般步骤:1.

随机推荐