python灰色预测法的具体使用

目录

• 1.简介
• 2.算法详解
• 2.1生成累加数据
• 2.2  累加后的数据表达式
• 2.3 求解2.2的未知参数
• 3.实例分析
• 3.1导入数据
• 3.2进行累加数据
• 3.3求解系数
• 3.4预测数据及对比

1.简介

灰色系统理论认为对既含有已知信息又含有未知或非确定信息的系统进行预测，就是对在一定方位内变化的、与时间有关的灰色过程的预测。尽管过程中所显示的现象是随机的、杂乱无章的，但毕竟是有序的、有界的，因此这一数据集合具备潜在的规律，灰色预测就是利用这种规律建立灰色模型对灰色系统进行预测。

灰色预测通过鉴别系统因素之间发展趋势的相异程度，即进行关联分析，并对原始数据进行生成处理来寻找系统变动的规律，生成有较强规律性的数据序列，然后建立相应的微分方程模型，从而预测事物未来发展趋势的状况。其用等时距观测到的反应预测对象特征的一系列数量值构造灰色预测模型，预测未来某一时刻的特征量，或达到某一特征量的时间。

2.算法详解

2.1 生成累加数据

2.2  累加后的数据表达式

2.3 求解2.2的未知参数

3.实例分析

现有1997—2002年各项指标相关统计数据如下表：

用灰色预测方法预测2003—2009年各项指标的数据。且已知实际的预测数据如下：将预测数据与实际数据进行比较

3.1 导入数据

#原数据
data=np.array([[72.03,241.2,1592.74],[73.84,241.2,1855.36],[74.49,244.8,2129.60],[76.68,250.9,2486.86],[78.00,250.9,2728.94],[79.68,252.2,3038.90]])
#要预测数据的真实值
data_T=np.array([[81.21,256.5,3458.05],[82.84,259.4,3900.27],[84.5,262.4,4399.06],[86.19,265.3,4961.62],[87.92,268.3,5596.1],[89.69,271.4, 6311.79],[91.49,274.5,7118.96]])

返回结果，请自行打印查看

3.2 进行累加数据

#累加数据
data1=np.cumsum(data.T,1) #按列相加
print(data1)

返回：

3.3 求解系数

[m,n]=data1.shape #得到行数和列数 m=3,n=6
#对这三列分别进行预测
X=[i for i in range(1997,2003)]#已知年份数据
X=np.array(X)
X_p=[i for i in range(2003,2010)]#预测年份数据
X_p=np.array(X_p)
X_sta=X[0]-1#最开始参考数据
#求解未知数
for j in range(3):
    B=np.zeros((n-1,2))
    for i in range(n-1):
        B[i,0]=-1/2*(data1[j,i]+data1[j,i+1])
        B[i,1]=1
    Y=data.T[j,1:7]
    a_u=np.dot(np.dot(np.linalg.inv(np.dot(B.T,B)),B.T),Y.T)
    print(a_u)
    #进行数据预测
    a=a_u[0]
    u=a_u[1]

返回：

得到3对 a和u

3.4 预测数据及对比

需在3.3的基础上进行预测

[m,n]=data1.shape #得到行数和列数 m=3,n=6
#对这三列分别进行预测
X=[i for i in range(1997,2003)]#已知年份数据
X=np.array(X)
X_p=[i for i in range(2003,2010)]#预测年份数据
X_p=np.array(X_p)
X_sta=X[0]-1#最开始参考数据
#求解未知数
for j in range(3):
    B=np.zeros((n-1,2))
    for i in range(n-1):
        B[i,0]=-1/2*(data1[j,i]+data1[j,i+1])
        B[i,1]=1
    Y=data.T[j,1:7]
    a_u=np.dot(np.dot(np.linalg.inv(np.dot(B.T,B)),B.T),Y.T)
#     print(a_u)
    #进行数据预测
    a=a_u[0]
    u=a_u[1]
    T=[i for i in range(1997,2010)]
    T=np.array(T)
    data_p=(data1[0,j]-u/a)*np.exp(-a*(T-X_sta-1))+u/a #累加数据
#     print(data_p)
    data_p1=data_p
    data_p1[1:len(data_p)]=data_p1[1:len(data_p)]-data_p1[0:len(data_p)-1]
#     print(data_p1)
    title_str=['第一产业GDP预测','居民消费价格指数预测','第三产业GDP预测']
    plt.subplot(221+j)
    data_n=data_p1
    plt.scatter(range(1997,2003),data[:,j])
    plt.plot(range(1997,2003),data_n[X-X_sta])
    plt.scatter(range(2003,2010),data_T[:,j])
    plt. plot(range(2003,2010),data_n[X_p-X_sta-1])
#     plt.title(title_str[j])
    plt.legend(['实际原数据','拟合数据','预测参考数据','预测数据'])
    y_n=data_n[X_p-X_sta-1].T
    y=data_T[:,j]
    wucha=sum(abs(y_n-y)/y)/len(y)
    titlestr1=[title_str[j],'预测相对误差：',wucha]
    plt.title(titlestr1)
    plt.show()

返回：

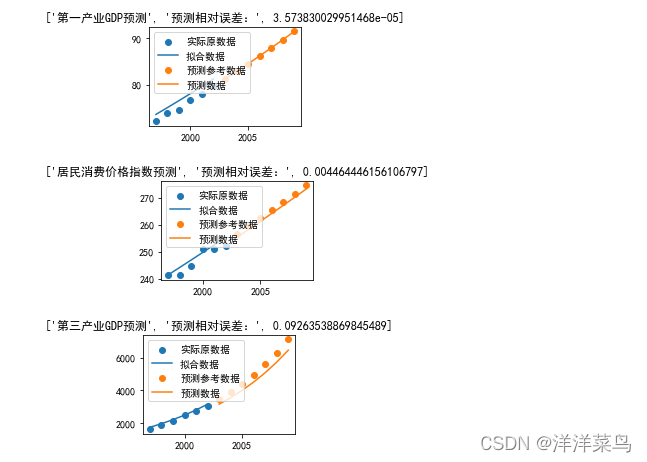
完整代码

import numpy as np
import matplotlib.pyplot as plt
import math

# 解决图标题中文乱码问题
import matplotlib as mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题

#原数据
data=np.array([[72.03,241.2,1592.74],[73.84,241.2,1855.36],[74.49,244.8,2129.60],[76.68,250.9,2486.86],[78.00,250.9,2728.94],[79.68,252.2,3038.90]])
#要预测数据的真实值
data_T=np.array([[81.21,256.5,3458.05],[82.84,259.4,3900.27],[84.5,262.4,4399.06],[86.19,265.3,4961.62],[87.92,268.3,5596.1],[89.69,271.4, 6311.79],[91.49,274.5,7118.96]])

#累加数据
data1=np.cumsum(data.T,1)
print(data1)

[m,n]=data1.shape #得到行数和列数 m=3,n=6
#对这三列分别进行预测
X=[i for i in range(1997,2003)]#已知年份数据
X=np.array(X)
X_p=[i for i in range(2003,2010)]#预测年份数据
X_p=np.array(X_p)
X_sta=X[0]-1#最开始参考数据
#求解未知数
for j in range(3):
    B=np.zeros((n-1,2))
    for i in range(n-1):
        B[i,0]=-1/2*(data1[j,i]+data1[j,i+1])
        B[i,1]=1
    Y=data.T[j,1:7]
    a_u=np.dot(np.dot(np.linalg.inv(np.dot(B.T,B)),B.T),Y.T)
#     print(a_u)
    #进行数据预测
    a=a_u[0]
    u=a_u[1]
    T=[i for i in range(1997,2010)]
    T=np.array(T)
    data_p=(data1[0,j]-u/a)*np.exp(-a*(T-X_sta-1))+u/a #累加数据
#     print(data_p)
    data_p1=data_p
    data_p1[1:len(data_p)]=data_p1[1:len(data_p)]-data_p1[0:len(data_p)-1]
#     print(data_p1)
    title_str=['第一产业GDP预测','居民消费价格指数预测','第三产业GDP预测']
    plt.subplot(221+j)
    data_n=data_p1
    plt.scatter(range(1997,2003),data[:,j])
    plt.plot(range(1997,2003),data_n[X-X_sta])
    plt.scatter(range(2003,2010),data_T[:,j])
    plt. plot(range(2003,2010),data_n[X_p-X_sta-1])
#     plt.title(title_str[j])
    plt.legend(['实际原数据','拟合数据','预测参考数据','预测数据'])
    y_n=data_n[X_p-X_sta-1].T
    y=data_T[:,j]
    wucha=sum(abs(y_n-y)/y)/len(y)
    titlestr1=[title_str[j],'预测相对误差：',wucha]
    plt.title(titlestr1)
    plt.show()

到此这篇关于python灰色预测法的具体使用的文章就介绍到这了,更多相关python灰色预测法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！