详解利用Flutter中的Canvas绘制有趣的图形

目录

• 简介
• 等边三角形构建重复之美
• 绘制彩虹
• 绘制五角星
• 总结

简介

上一篇我们介绍了使用 Flutter 的 Canvas 绘制基本图形的示例，简单的示例没什么好玩的，今天这一篇我们来点有趣的，我们会完成如下图形的绘制：

• 发现数学重复之美：使用等边三角形组合成彩虹伞面。
• 绘制彩虹。
• 绘制评分用的五角星。

通过这一篇，我们可以知道自定义形状绘制的基本原理，然后可以在这个基础上绘制你自己想要绘制的图形。

等边三角形构建重复之美

首先我们来绘制等边三角形，其实上一篇我们也有绘制等边三角形，只是那是将三个顶点手动计算出来的，这一篇我们封装一个绘制等边三角形的通用方法。老规矩，先定义方法的输入参数，如下所示：

• canvas：Canvas 画布
• color：绘制颜色
• startVertex：三角形的第一个顶点位置，这里我们其他边都是相对这个点旋转的
• length：边长
• startAngle：第一条边相对水平方向旋转的夹角，这样我们可以改变夹角来更改三角形的绘制位置。
• clockwise：顺时针绘制，如果是顺时针，则绘制的偏移夹角往顺时针方向开始，否则逆时针。
• filled：是否填充图形。

void drawEquilateralTriangle(
    Canvas canvas, {
    required Color color,
    required Offset startVertex,
    required double length,
    double startAngle = 0,
    clockwise = true,
    filled = true,
  })

等边三角形基于一个顶点，一条边和起始角度后就可以计算其他两个顶点的位置，具体推到通过三角函数就可以了。

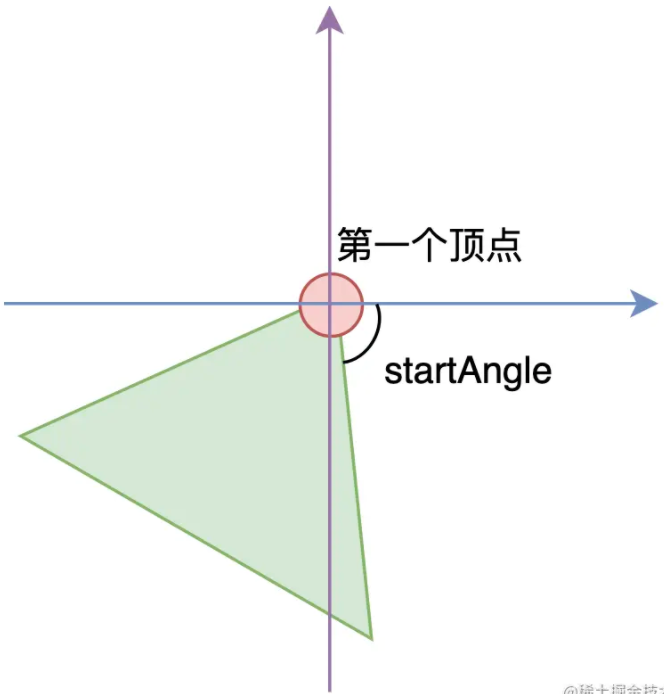
具体计算三角形的三个顶点的方法如下，这里逆时针方向和顺时针方向的计算方式有点不同，需要区分一下。

static List<Offset> getEquilateralTriangleVertexes(
      Offset startVertex, double length,
      {double startAngle = 0, bool clockwise = true}) {
  double point2X, point2Y, point3X, point3Y;
  point2X = startVertex.dx + length * cos(startAngle);
  point2Y = startVertex.dy - length * sin(startAngle);
  if (clockwise) {
    point3X = startVertex.dx + length * cos(pi / 3 + startAngle);
    point3Y = startVertex.dy - length * sin(pi / 3 + startAngle);
  } else {
    point3X = startVertex.dx + length * cos(pi / 3 - startAngle);
    point3Y = startVertex.dy + length * sin(pi / 3 - startAngle);
  }

  return [startVertex, Offset(point2X, point2Y), Offset(point3X, point3Y)];
}

有了顶点我们就可以使用 Path 将顶点连起来就完成等边三角形的绘制了，绘制三角形的实现方法如下：

void drawEquilateralTriangle(
    Canvas canvas, {
    required Color color,
    required Offset startVertex,
    required double length,
    double startAngle = 0,
    clockwise = true,
    filled = true,
  }) {
    assert(length > 0);
    Path trianglePath = Path();
    List<Offset> vertexes = ShapesUtil.getEquilateralTriangleVertexes(
      startVertex,
      length,
      clockwise: clockwise,
      startAngle: startAngle,
    );
    trianglePath.moveTo(vertexes[0].dx, vertexes[0].dy);
    for (int i = 1; i < vertexes.length; i++) {
      trianglePath.lineTo(vertexes[i].dx, vertexes[i].dy);
    }
    trianglePath.close();
    Paint paint = Paint();
    paint.color = color;
    if (!filled) {
      paint.style = PaintingStyle.stroke;
    }
    canvas.drawPath(trianglePath, paint);
  }
}

单独一个三角形没啥意思，我们通过画6个等边三角形，每个三角形旋转60度，空心绘制看看怎么样？

一个 完美的六边形出来了，再试试12个怎么样。

形状越多，会越接近圆形，你会充分发现对称之美。下面是我们用24个三角形，填充不同颜色后的效果。有点像一把彩虹伞的伞面了，感觉是不是很美？

上面图形的实现代码如下，其中颜色是通过一个颜色数组完成的。

int number = 24;
for (int i = 0; i < number; ++i) {
  drawEquilateralTriangle(
    canvas,
    color: colors[i],
    startVertex: Offset(center.width, center.height),
    length: 120,
    startAngle: i * 2 * pi / number,
    clockwise: true,
    filled: true,
  );
}

绘制彩虹

有了上面的彩虹伞一样的启发，我们决定来绘制彩虹。彩虹其实比较简单，绘制7条不同颜色的弧线即可。这里讲一下弧线的绘制约束。如下图所示，实际上弧线是通过矩形的内接椭圆限制的（这里用正方形，内接为圆形示例）。外面的矩形限制了椭圆位置和尺寸，而通过 startAngle (起始角度）和 sweepAngle (弧线覆盖的角度范围）就能够确定弧线的起点和终点，从而得到一段弧线。注意的是，数学里我们是逆时针角度为正，但是在 Flutter 默认是顺时针为正，因此如果你要从逆时针方向开始角度就要设置为负数。

下面是弧线绘制的示例代码：

Path path1 = Path();
Rect rect1 = Rect.fromLTWH(startPoint.dx + (width - innerWidth) / 2,
    startPoint.dy + (width - innerWidth) / 2, innerWidth, innerWidth);
path1.arcTo(rect1, -pi / 6, -2 * pi / 3, true);
paint.color = colors[i];
canvas.drawPath(path1, paint);

有了这个基础，我们通过循环 ，绘制7条弧线，保证每条弧线挨着就行。而弧线的线条粗细可以用画笔的宽度来搞定，代码如下。我们这里每条弧线的中心、起始角度和覆盖角度是一样的，通过改变不同弧线的正方形边长实现彩虹弧线的位置不同，然后画笔粗细保持为每条彩虹的高度的一半就可以保证每条彩虹是挨着的了。

void drawRainbow(
    Canvas canvas, {
    required Offset startPoint,
    required double width,
  }) {
  assert(width > 0);
  var paint = Paint();
  double rowHeight = 12;
  paint.strokeWidth = rowHeight / 2;
  List<Color> colors = [
    Color(0xFFE05100),
    Color(0xFFF0A060),
    Color(0xFFE0E000),
    Color(0xFF10F020),
    Color(0xFF2080F5),
    Color(0xFF104FF0),
    Color(0xFFA040E5),
  ];
  paint.style = PaintingStyle.stroke;
  for (var i = 0; i < 7; i++) {
    double innerWidth = width - i * rowHeight;
    Path path1 = Path();
    Rect rect1 = Rect.fromLTWH(startPoint.dx + (width - innerWidth) / 2,
        startPoint.dy + (width - innerWidth) / 2, innerWidth, innerWidth);
    path1.arcTo(rect1, -pi / 6, -2 * pi / 3, true);
    paint.color = colors[i];
    canvas.drawPath(path1, paint);
  }
}

最终效果如下图所示。

绘制五角星

五角星相对来说会复杂一些，主要是要知道通过中心点确定10个顶点的坐标，这里就需要利用二维坐标的旋转公式了，具体可以查阅相关资料，结论是一个点(x2, y2)围绕另一个点(x1, y1)旋转某个角度（α）后得到的新坐标(x, y)计算方式如下：

x=x1+(x2-x1)*cos(α)-(y2-y1)*sin(α)

y=y1+(y2-y1)*cos(α)+(x2-x1)*sin(α)

有了这个基础，我们就可以基于五角星的中心点，第一个顶点，边长（间隔一个点连线的线段长度）来通过旋转计算其他顶点了。其中外面5顶点一组计算，内部5个顶点一组计算。最终获取5个顶点的代码如下：

static List<Offset> getStarVertexes(Offset center, double length) {
  assert(length > 0);
  // 外接圆半径计算（五角星锐角为36度）
  double radius = length / 2 / cos(18 / 180 * pi);
  // 内部顶点的半径
  double innerRadius =
      radius / (cos(36 / 180 * pi) + sin(36 / 180 * pi) / sin(18 / 180 * pi));
  List<Offset> vertexes = [];
  Offset outerStartVertex = Offset(center.dx, center.dy - radius);
  Offset innerStartVertex = Offset(
    center.dx - innerRadius * sin(36 / 180 * pi),
    center.dy - innerRadius * cos(36 / 180 * pi),
  );
  vertexes.add(outerStartVertex);
  vertexes.add(innerStartVertex);
  // 计算方式为以第一个顶点围绕五角星中心点坐标旋转得到
  const double rotateAngle = 72 / 180 * pi;
  for (int i = 1; i < 5; ++i) {
    vertexes.add(Offset(
      center.dx +
          (outerStartVertex.dx - center.dx) * cos(-i * rotateAngle) -
          (outerStartVertex.dy - center.dy) * sin(-i * rotateAngle),
      center.dy +
          (outerStartVertex.dy - center.dy) * cos(-i * rotateAngle) +
          (outerStartVertex.dx - center.dx) * sin(-i * rotateAngle),
    ));
    vertexes.add(Offset(
      center.dx +
          (innerStartVertex.dx - center.dx) * cos(-i * rotateAngle) -
          (innerStartVertex.dy - center.dy) * sin(-i * rotateAngle),
      center.dy +
          (innerStartVertex.dy - center.dy) * cos(-i * rotateAngle) +
          (innerStartVertex.dx - center.dx) * sin(-i * rotateAngle),
    ));
  }

  return vertexes;
}

有了顶点，绘制方式就和三角形一样了，将顶点连起来就好了。下面是我们绘制了一个常见的五星评分的图形。

总结

本篇介绍了基于 Flutter 的 CustomPaint 绘制定制化图形的示例，可以看到，其实只要 UI 小姐姐给出的图形能够用数学表达式表示出来，都可以用 CustomPaint 的 Canvas 来实现。

到此这篇关于详解利用Flutter中的Canvas绘制有趣的图形的文章就介绍到这了,更多相关Flutter Canvas图形内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！