基于Matlab绘制小提琴图的示例代码

目录

• violinChart 函数使用方法
• 基础使用，Y为矩阵
• 基础使用，Y为向量，X为标签
• 基础使用，多个图像绘制，并添加图例
• violinChart 完整函数
• ggtheme violin 函数介绍
• ggtheme violin 主题
• ggtheme violin 修饰函数代码

本文将为大家详细讲解Matlab中小提琴图的绘制函数及ggtheme主题修饰函数

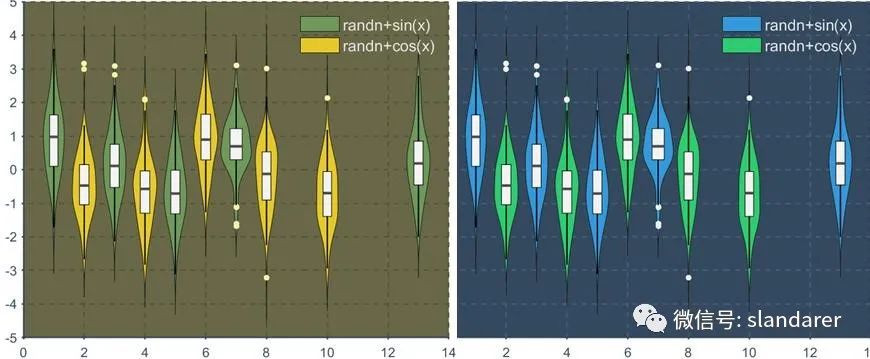
violinChart 函数使用方法

写了个matlab绘制小提琴图的函数：

1.图中小提琴状区域为核密度曲线。

2.白色方块为25%，75%分位数。

3.中间横线为中位数。

4.白色点为离群值点。

5.竖着的黑线是去掉离群值点后点的上下限。

基础使用，Y为矩阵

X=1:5;
Y=randn(100,5);

violinChart(gca,X,Y,[0 0.447 0.741],0.6);

• X | 横坐标。
• Y | 数据集。
• FaceColor | 颜色，示例用的是[0 0.447 0.741]。
• width | 小提琴图宽度，这里取的是0.6,就是以两个小提琴图间距的0.6倍为概率密度的上限1。

基础使用，Y为向量，X为标签

X=[1.*ones(1,50),2.*ones(1,30),3.*ones(1,20),4.*ones(1,50),5.*ones(1,50)];
Y=randn(1,200)+sin(X);

violinChart(gca,X,Y,[0 0.447 0.741]);

基础使用，多个图像绘制，并添加图例

X1=[1:2:7,13];
Y1=randn(100,5)+sin(X1);
X2=2:2:10;
Y2=randn(100,5)+cos(X2);

figure
Hdl1=violinChart(gca,X1,Y1,[0     0.447 0.741]);
Hdl2=violinChart(gca,X2,Y2,[0.850 0.325 0.098]);
legend([Hdl1.F_legend,Hdl2.F_legend],{'randn+sin(x)','randn+cos(x)'});

violinChart 完整函数

若函数有更新则会将更新版本放入文末所示压缩文件内。

function Hdl=violinChart(ax,X,Y,FaceColor,width)
% @author slandarer
% Hdl: 返回的图形对象句柄结构体
% - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
% Hdl.F_density(i)   | patch   | 核密度分布
% Hdl.F_outlier(i)   | scatter | 离群值点
% Hdl.F_range95(i)   | line    | 去除离群值点后最大值及最小值
% Hdl.F_quantile(i)  | patch   | 四分位数框
% Hdl.F_medianLine(i)| line    | 中位数
%
% Hdl.F_legend       | patch   | 用于生成legend图例的图形对象
% - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
% 请使用如下方式生成图例：
% Hdl1=violinChart(ax,X,Y,... ...)
% Hdl2=violinChart(ax,X,Y,... ...)
% ... ...
% legend([Hdl1,Hdl2,... ...],{Name1,Name2,...})
% ===========================================================
% 以下为使用实例代码：
% - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
% X1=[1:2:7,13];
% Y1=randn(100,5)+sin(X1);
% X2=2:2:10;
% Y2=randn(100,5)+cos(X2);
%
% Hdl1=violinChart(gca,X1,Y1,[0     0.447 0.741],0.5);
% Hdl2=violinChart(gca,X2,Y2,[0.850 0.325 0.098],0.5);
% legend([Hdl1.F_legend,Hdl2.F_legend],{'randn+sin(x)','randn+cos(x)'});

if nargin<5
    width=0.4;
end

if ~isempty(ax)
else
    ax=gca;
end
hold(ax,'on');

oriX=X;
X=unique(X);
sep=min(diff(X));
if isempty(sep)
    sep=1;
end
for i=1:length(X)
    if length(oriX)==numel(Y)
        tY=Y(oriX==X(i));
    else
        tY=Y(:,i);
    end
    [f,yi]=ksdensity(tY);
    Hdl.F_density(i)=fill([f,-f(end:-1:1)].*sep.*width+X(i),[yi,yi(end:-1:1)],FaceColor);

    outliBool=isoutlier(tY,'quartiles');
    outli=tY(outliBool);
    Hdl.F_outlier(i)=scatter(repmat(X(i),[length(outli),1]),outli,20,'filled',...
                    'CData',[1 1 1],'MarkerEdgeColor','none');
    nY=tY(~outliBool);
    Hdl.F_range95(i)=plot([X(i),X(i)],[min(nY),max(nY)],'k','lineWidth',1);

    qt25=quantile(tY,0.25);
    qt75=quantile(tY,0.75);

    Hdl.F_quantile(i)=fill(X(i)+0.6.*sep.*width.*[-1 1 1 -1].*max(f),...
                    [qt25,qt25,qt75,qt75],[1 1 1],...
                    'EdgeColor',[0 0 0]);

    med=median(tY);
    Hdl.F_medianLine(i)=plot(X(i)+0.6.*sep.*width.*[-1 1].*max(f),[med,med],'LineWidth',3,...
                    'Color',[0 0 0]);
end

Hdl.F_legend=Hdl.F_density(1);
end

ggtheme violin 函数介绍

假设你已经编写了上述绘图代码，只需要将最后增添一行变为

X1=[1:2:7,13];
Y1=randn(100,5)+sin(X1);
X2=2:2:10;
Y2=randn(100,5)+cos(X2);

figure
Hdl1=violinChart(gca,X1,Y1,[0     0.447 0.741]);
Hdl2=violinChart(gca,X2,Y2,[0.850 0.325 0.098]);
legend([Hdl1.F_legend,Hdl2.F_legend],{'randn+sin(x)','randn+cos(x)'});

ggThemeViolin(gca,[Hdl1,Hdl2],'dust');

则图像会被修饰：

而将函数最后加入‘LP’参数则变为：

ggThemeViolin(gca,[Hdl1,Hdl2],'dust','LP');

ggtheme violin 主题

主题有如下选择：

'flat'/'flat_dark'/'camouflage'/'chalk'/
'copper'/'dust'/'earth'/'fresh'/'grape'/
'grass'/'greyscale'/'light'/'lilac'/'pale'/
'sea'/'sky'/'solarized'

'flat'

'flat_dark'

'camouflage'

'chalk'

'copper'

'dust'

'earth'

'fresh'

'grape'

'grass'

'greyscale'

'light'

'lilac'

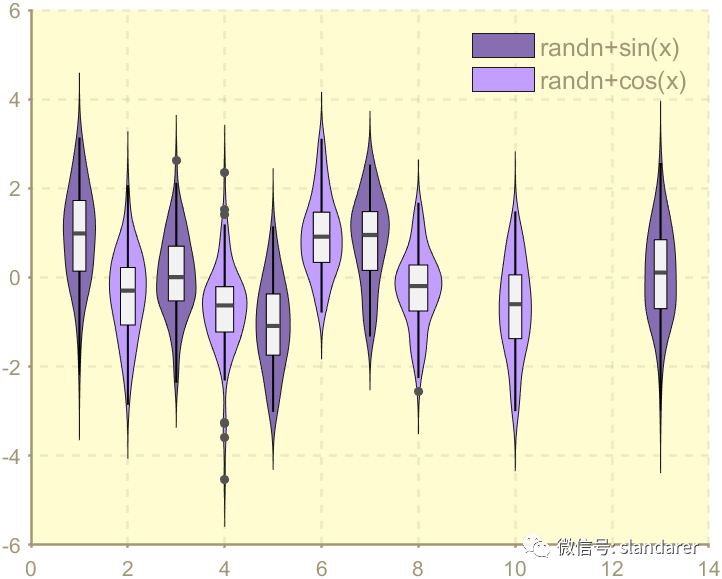
'pale'

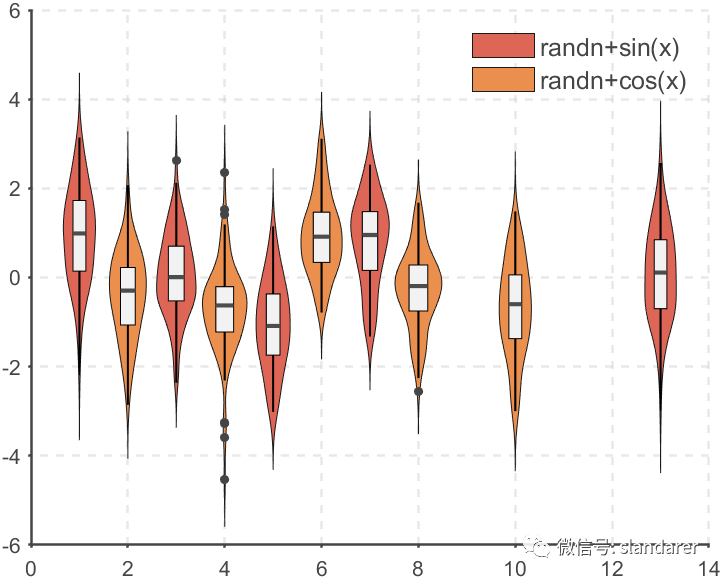
'sea'

'sky'

'solarized'

ggtheme violin 修饰函数代码

注意，要使用ggThemeViolin修饰器函数，需要保证当前文件夹有themeCSS.mat文件，该文件将会一同在压缩包内给出。

function ax=ggThemeViolin(varargin)
% @author:slandarer
%
% 参数说明：
% -----------------------------------------------------
% AxesTheme   | 坐标区域风格       | 'flat'/'flat_dark'/'camouflage'/'chalk'/
%                                    'copper'/'dust'/'earth'/'fresh'/'grape'/
%                                    'grass'/'greyscale'/'light'/'lilac'/'pale'
%                                    'sea'/'sky'/'solarized'
%
% HDLset      | 句柄集合    

% 获取要处理的坐标区域=====================================================
if strcmp(get(varargin{1},'type'),'axes' )
    ax=varargin{1};
else
    ax=gca;
end
hold(ax,'on')

% 获取要处理的图像句柄=====================================================
HDLset=varargin{2};

% 获取风格名称=============================================================
theme.AxesTheme='flat';
if length(varargin)>2
    theme.AxesTheme=varargin{3};
end

% 开始风格化===============================================================
ax.Box='off';
ax.YGrid='on';
ax.XGrid='on';
ax.GridLineStyle='--';
ax.LineWidth=1.2;

% 主题风格化
Tm=load('themeCSS.mat');
Tm=Tm.theme;
ax.Color=Tm.(theme.AxesTheme).Color;
ax.TickLength=Tm.(theme.AxesTheme).TickLength;
ax.GridColorMode=Tm.(theme.AxesTheme).GridColorMode;
ax.GridColor=Tm.(theme.AxesTheme).GridColor;
ax.GridAlpha=Tm.(theme.AxesTheme).GridAlpha;
ax.XColor=Tm.(theme.AxesTheme).XColor;
ax.YColor=Tm.(theme.AxesTheme).YColor;
ax.TickDir=Tm.(theme.AxesTheme).TickDir;
ax.ColorOrder=Tm.(theme.AxesTheme).ColorOrder;

for i=1:length(HDLset)
    for j=1:length(HDLset(i).F_density)
        HDLset(i).F_density(j).FaceColor=ax.ColorOrder(mod(i-1,size(ax.ColorOrder,1))+1,:);
        HDLset(i).F_density(j).EdgeColor=[.1,.1,.1];

        f_max=(max(HDLset(i).F_density(j).XData)-min(HDLset(i).F_density(j).XData))/2;
        x_mid=(max(HDLset(i).F_density(j).XData)+min(HDLset(i).F_density(j).XData))/2;
        HDLset(i).F_quantile(j).XData=x_mid+0.4.*f_max.*[-1 1 1 -1];
        HDLset(i).F_quantile(j).FaceColor=[1 1 1].*0.95;

        HDLset(i).F_medianLine(j).XData=x_mid+0.4.*f_max.*[-1 1];
        HDLset(i).F_medianLine(j).LineWidth=2;
        HDLset(i).F_medianLine(j).Color=[0.3,0.3,0.3];

        HDLset(i).F_outlier(j).CData=Tm.(theme.AxesTheme).EdgeColor;
    end

end

if ~isempty(ax.Legend)
    ax.Legend.Box='off';
    ax.Legend.FontSize=12;
    if mean(ax.Color)>0.6
        ax.Legend.TextColor=ax.XColor;
    else
        ax.Legend.TextColor=[0.9 0.9 0.9];
    end
    if ~isempty(regexpi(ax.Legend.Location,'out', 'once'))
        ax.Legend.TextColor=ax.XColor;
        ax.Legend.Title.FontSize=14;
    end
    ax.Legend.AutoUpdate='off';
end

end

到此这篇关于基于Matlab绘制小提琴图的示例代码的文章就介绍到这了,更多相关Matlab小提琴图内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！