Python使用scipy.fft进行大学经典的傅立叶变换

傅里叶变换是在高数是一个很重要的知识点，今天将结合Python代码实现傅立叶变换。

傅立叶变换

我们平时是如何去分解一个复杂的问题呢？一个经典的方法就是把这个复杂的问题分解成为多个简单的可操作的子问题， 傅立叶变换也是基于这个思想。

傅里叶分析是研究如何将数学函数分解为一系列更简单的三角函数的领域。傅里叶变换是该领域的一种工具，用于将函数分解为其分量频率。

在本教程中，傅立叶变换是一种工具，可以获取信号并查看其中每个频率的功率。看一看该傅立叶变换中的重要术语：

• 信号：信号是随时间变化的信息。例如，音频，视频和电压走线都是信号的示例。
• 频率：频率是某物重复的速度。例如，时钟以1赫兹（Hz）的频率滴答，或每秒重复1次。
• 功率：功率表示每个频率的强度。

下图是一些正弦波的频率和功率的直观演示：

第一个是低频正弦波，第二个是高频正弦波，第三个是低频低功率正弦波，因此低功率正弦波比其它两个正弦波的峰较小。

时域与频域

时域与频域是查看信号的两种不同方式，即信号的组成频率或随时间变化的信息。

在时域中，信号是随时间（x轴）幅度（y轴）变化的波。您最有可能在时域中查看图表，例如：

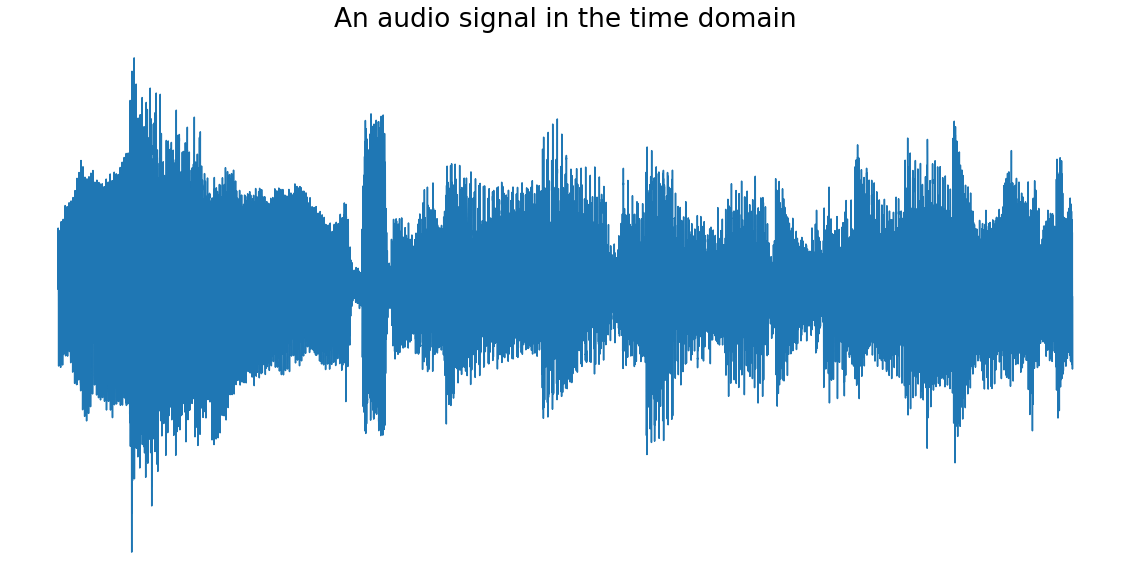
这是一些音频的图像，它是一个时域信号。横轴表示时间，纵轴表示振幅。

在频域中，信号表示为一系列频率（x轴），每个频率都具有关联的功率（y轴）。下图是经过傅立叶变换后的上述音频信号：

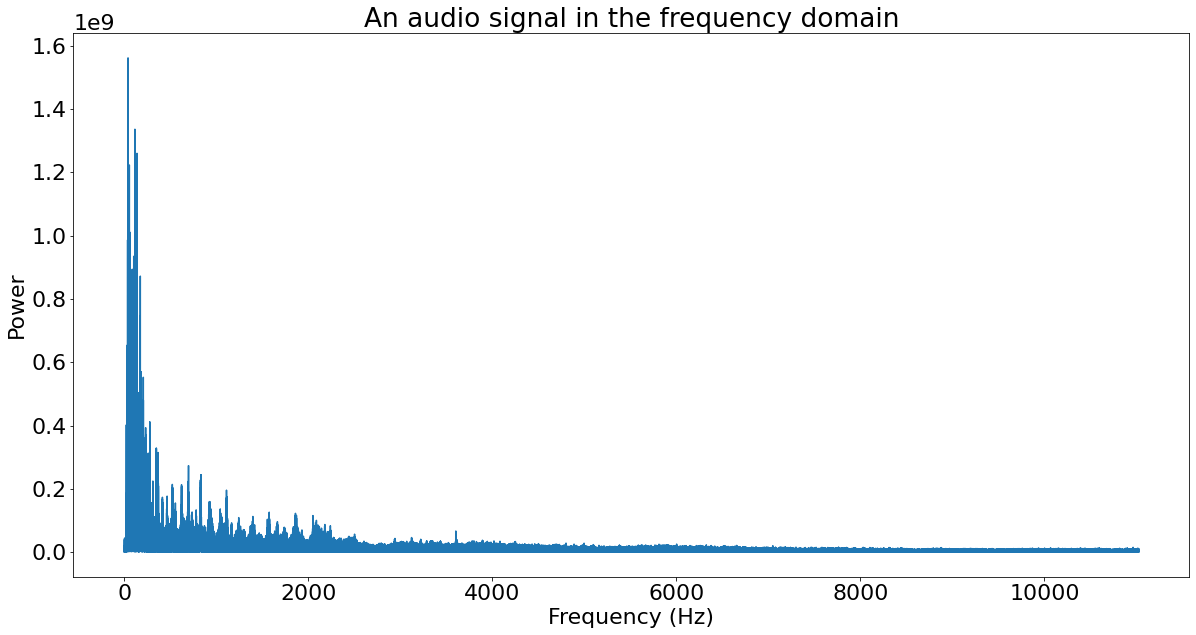
代码实现正弦波

音频本质上是正弦波。

下面是产生正弦波的代码：

import numpy as np
from matplotlib import pyplot as plt

SAMPLE_RATE = 44100  # 赫兹
DURATION = 5  # 秒

def generate_sine_wave(freq, sample_rate, duration):
    x = np.linspace(0, duration, sample_rate * duration, endpoint=False)
    frequencies = x * freq

    y = np.sin((2 * np.pi) * frequencies)
    return x, y

# 产生持续5秒的2赫兹正弦波
x, y = generate_sine_wave(2, SAMPLE_RATE, DURATION)
plt.plot(x, y)
plt.show()

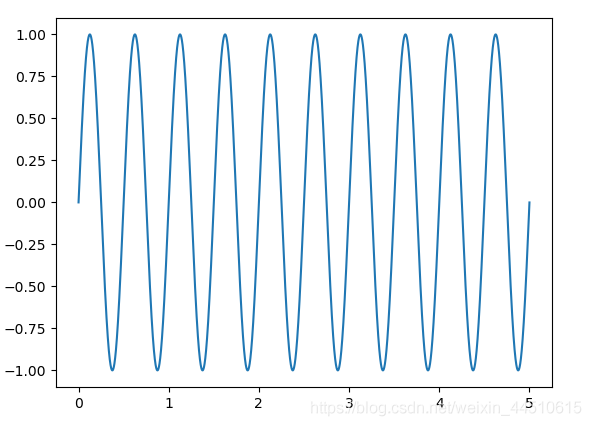
x轴以秒为单位表示时间，并且由于每秒钟的时间都有两个峰值，因此可以看到正弦波每秒振荡两次。

混合音频

下面将两个正弦波，混合音频信号仅包括两个步骤：

将正弦波加在一起，然后进行归一化的操作。

具体实现的代码如下。

_, nice_tone = generate_sine_wave(400, SAMPLE_RATE, DURATION)
_, noise_tone = generate_sine_wave(4000, SAMPLE_RATE, DURATION)
noise_tone = noise_tone * 0.3

mixed_tone = nice_tone + noise_tone

下一步是归一化，或缩放信号以适合目标格式。由于以后将如何存储音频，目标格式为16位整数，范围为-32768到32767：

normalized_tone = np.int16((mixed_tone / mixed_tone.max()) * 32767)

plt.plot(normalized_tone[:1000])
plt.show()

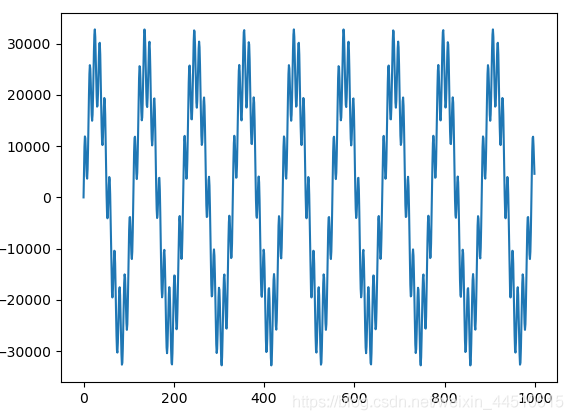
看到的正弦波是生成的400 Hz音调，将上面的正弦波转化为音频，最简单的方法是使用SciPy的wavfile.write方法将其存储在WAV文件中。16位整数是WAV文件的标准数据类型，因此需要将信号标准化为16位整数：

from scipy.io.wavfile import write

# 记住，采样率=44100赫兹是我们的播放率
write("mysinewave.wav", SAMPLE_RATE, normalized_tone)

这个音频听起来音调很高。

完成此步骤后，就当作音频样本了。下一步是使用傅立叶变换消除高音调！

傅立叶变换

现在对生成的音频上使用FFT了。FFT是一种算法，可实现傅立叶变换并可以在时域中为信号计算频谱。

from scipy.fft import fft, fftfreq

# 标准化音调中的样本数
N = SAMPLE_RATE * DURATION

yf = fft(normalized_tone)
xf = fftfreq(N, 1 / SAMPLE_RATE)

plt.plot(xf, np.abs(yf))
plt.show()

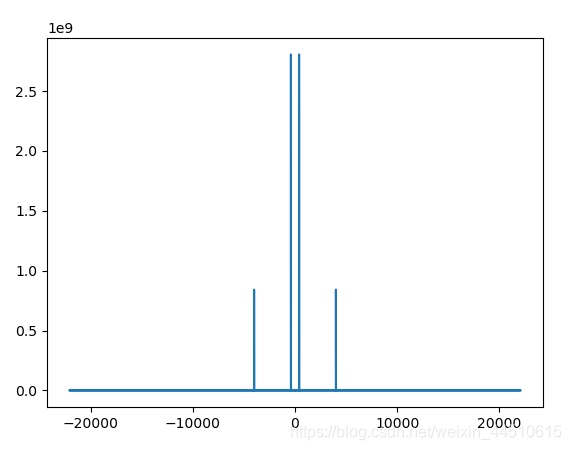
我们可以在正频率中看到两个峰值，正频率峰值位于400 Hz和4000 Hz，与之前生成的音频的频率相对应。

计算傅里叶变换

yf = fft(normalized_tone)
xf = fftfreq(N, 1 / SAMPLE_RATE)

上面代码的功能

• fft() 计算转换本身。
• fftfreq()计算的输出中每个仓中心的频率fft()。没有这个，就无法在频谱上绘制x轴

fft()输出的频谱围绕y轴反射，因此负半部分是正半部分的镜像，我们一般只需计算一半对称值，即可更快地进行傅立叶变换。scipy.fft以的形式实施此速度骇客rfft()。

from scipy.fft import rfft, rfftfreq

# 注意前面多余的“r”
yf = rfft(normalized_tone)
xf = rfftfreq(N, 1 / SAMPLE_RATE)

plt.plot(xf, np.abs(yf))
plt.show()

过滤信号

傅里叶变换的一大优点是它是可逆的，我们可以利用此优势来过滤音频并摆脱高音调频率。

# 最大频率为采样率的一半
points_per_freq = len(xf) / (SAMPLE_RATE / 2)

# 我们的目标频率是4000赫兹 将44100变成4000
target_idx = int(points_per_freq * 4000)

然后，您可以将其设置yf为0目标频率附近的index来摆脱它：

yf[target_idx - 1 : target_idx + 2] = 0

plt.plot(xf, np.abs(yf))
plt.show()

由于只有一个高峰，下面应用傅立叶逆变换返回时域。

应用逆FFT与应用FFT相似：

from scipy.fft import irfft

new_sig = irfft(yf)

plt.plot(new_sig[:1000])
plt.show()

由于您正在使用rfft()，因此需要使用irfft()来应用反函数。但是，如果您使用过fft()，则反函数将是ifft()。现在，您的绘图应如下所示：

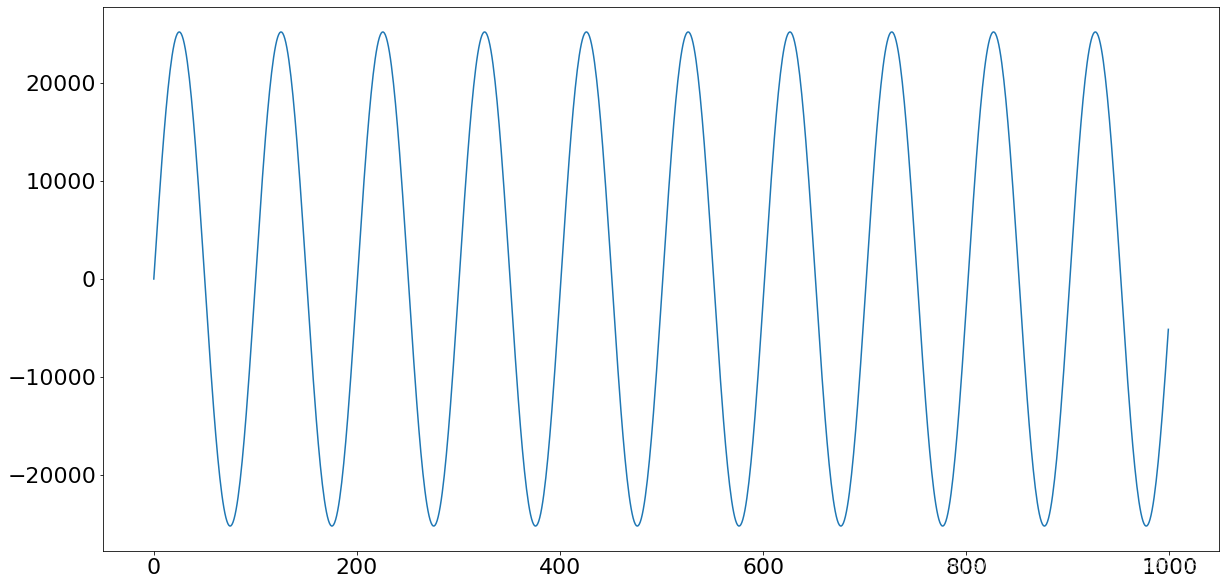
现在有一个以400 Hz振荡的正弦波，并且您已经成功地消除了4000 Hz的噪声。

对信号进行归一化，然后再将其写入文件。

norm_new_sig = np.int16(new_sig * (32767 / new_sig.max()))

write("clean.wav", SAMPLE_RATE, norm_new_sig)

到此这篇关于Python使用scipy.fft进行大学经典的傅立叶变换的文章就介绍到这了,更多相关Python 傅立叶变换内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！