R语言实现广义线性回归模型

目录
  • 1 与广义线性模型有关的R函数
  • 2 正态分布族
  • 3 二项分布族
    • 例  R. Norell实验

广义线性模型（GLM）是常见正态线性模型的直接推广，它可以适用于连续数据和离散数据，特别是后者，如属性数据、计数数据。这在应用上，尤其是生物、医学、经济和社会数据的统计分析上，有着重要意义。

对于广义线性模型应有一下三个概念：

  • 第一是线性自变量，它表明第i个响应变量的期望值E(yi)只能通过线性自变量βTxi而依赖于xi，其中如通常一样，β是未知参数的(p+1)x1向量，可能包含截距。
  • 第二是连续函数，它说明线性自变量和E(yi)的关系，给出了线性模型的推广。
  • 第三是误差函数，它说明广义线性模型的最后一部分随机成分。

我们保留样本为相互独立的假设，但去掉可加和正态误差的假设。可以从指数型分布族中作选一个作为误差函数。

1 与广义线性模型有关的R函数

R软件提供了拟合计算广义线性模型的函数glm()，其命令格式如下：

其中：

  • formula是拟合公式，这里的意义与线性模型相同，
  • family是分布族，即前面讲到的广义线性模型的种类，如正态分布，Poisson分布，二项分布等。
  • data是数据框，这里的意义与线性模型相同。

对于每个分布族（family），提供了相应的连接函数，如表6.12所示：

有了这些分布族和连接函数，我么就可以完成相应的广义线性模型的拟合问题。

2 正态分布族

正态分布族的使用方法是：

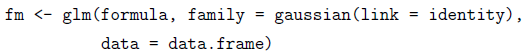
式中link=identity可以不写，因为正态分布族的连接函数缺省值是恒等（identity）。事实上，整个参数family = gaussian也可以不写，因为分布族的缺省值就是正态分布。

从表6.11可以看出，正态分布族的广义线性模型实际上与线性模型是相同的，也就是说：

与线性模型

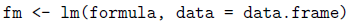
有完全相同的计算结果，但效率却低的多。

3 二项分布族

在二项分布族中，logistic回归模型是最重要的模型。在某些回归问题中，相应变量使分类的，经常是或者成功，或者失败。对于这些问题，正态线性模型显然是不合适的，因为正态误差不对应一个0-1相应。在这种情况下，可用一种重要的方法称为logistic回归。

用R软件计算logistic回归模型的公式为：

式中link=logit可以不写，因为logit是二项分布族连接函数是缺省状态。

在用glm()函数做logistic回归模型使，对于公式formula有两种输入方法，一种是输入成功和失败的次数，另一种像线性模型通常数据的输入方式。

例  R. Norell实验

为研究高压电线对牲畜的影响，R.Norell研究小的电流对农场动物的影响。他在实验中，选择了7头，6种电流强度，0,1,2,3,4,5毫安。每头牛被点击30下，每种强度5下，按随机的次序进行。然后重复整个实验，每头牛总共被点击60下。对每次电击，相应变量——嘴巴运动，或者出现，或者未出现。表6.13中的数据给出每种电击强度70次实验中相应的总次数。试分析电击对牛的影响。

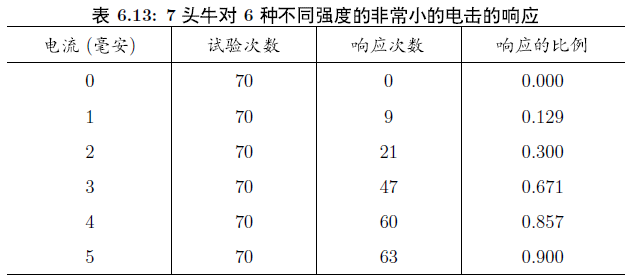
解：用数据框形式输入数据，在构造矩阵，一列是成功（响应）的次数，另一列是失败（不响应）的次数，然后在做logistic回归。其程序如下：

首先构造出的数据框如下：

对构造好的数据框进行处理如下：

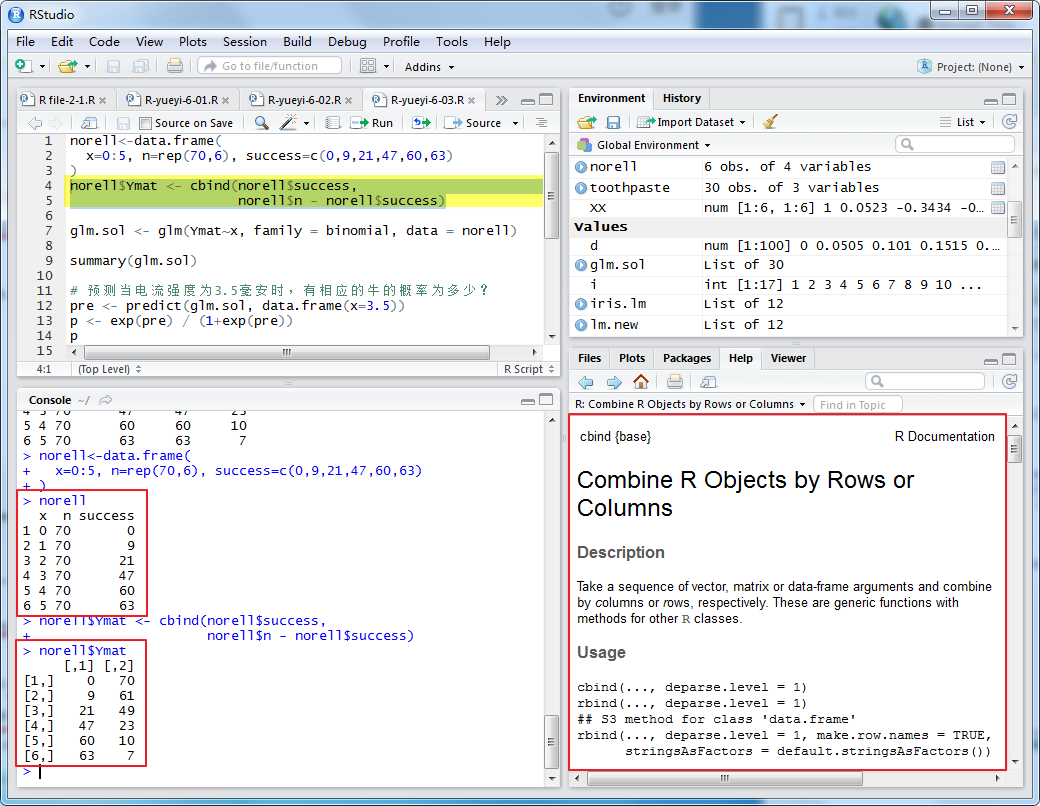
构建logistic模型如下：

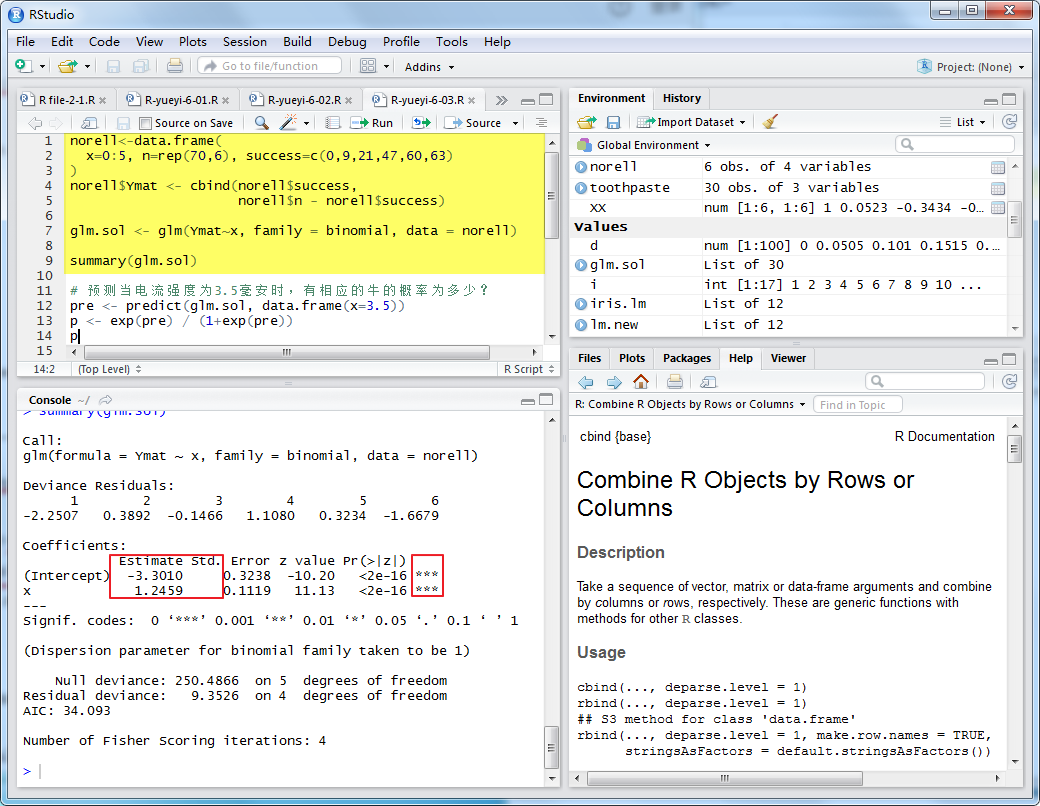
与线性回归模型相同，在得到回归模型后，可以作出预测。例如，当电流强度为3.5毫安时，有相应的牛的概率为多少？

即：74.26%。

可以作出控制，如有50%的牛有相应，其电流强度为多少？

即：2.65毫安的电流强度，可以使50%的牛有响应。

最后画出相应的比例与logistic回归曲线。R软件的绘图命令如下：

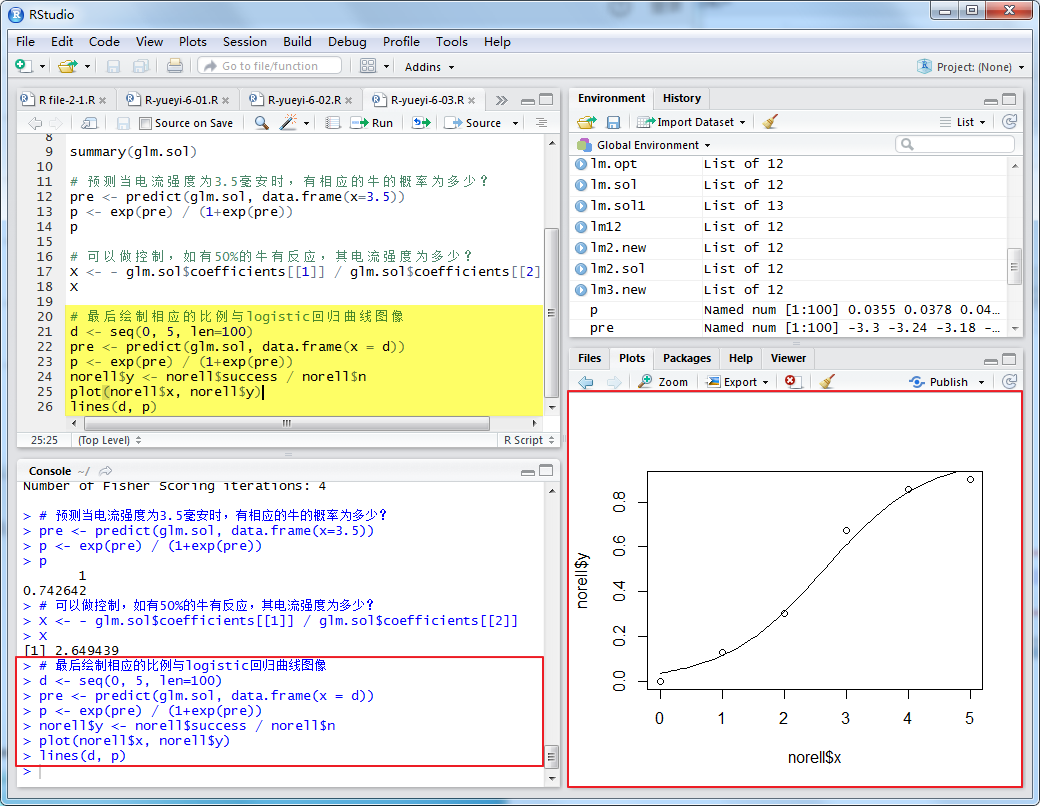
在程序中，d是给出曲线横坐标的点，pre是计算预测值，p是相应的预测概率。用plot函数和lines函数给出散点图和对应的预测曲线。

到此这篇关于R语言实现广义线性回归模型的文章就介绍到这了,更多相关R语言 广义线性回归模型内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • R语言如何实现多元线性回归

    R语言如何实现多元线性回归

    R小白几天的摸索 红色为输入,蓝色为输出 输入数据 先把数据用excel保存为csv格式放在"我的文档"文件夹 打开R软件,不用新建,直接写 回归计算 求三个平方和 置信区间(95%) 散点图(最显著的因变量) 拟合图 一元线性回归 结果:(看图) 变量系数  Estimate 变量系数标准误  Std. Error T检验值  t value T检验p值  Pr(>|t|) 均方根误差  Residual standard error 判定系数  R-squared 调整判定系

  • R语言线性回归知识点总结

    R语言线性回归知识点总结

    回归分析是一种非常广泛使用的统计工具,用于建立两个变量之间的关系模型. 这些变量之一称为预测变量,其值通过实验收集. 另一个变量称为响应变量,其值从预测变量派生. 在线性回归中,这两个变量通过方程相关,其中这两个变量的指数(幂)为1.数学上,线性关系表示当绘制为曲线图时的直线. 任何变量的指数不等于1的非线性关系将创建一条曲线. 线性回归的一般数学方程为 y = ax + b 以下是所使用的参数的描述 y是响应变量. x是预测变量. a和b被称为系数常数. 建立回归的步骤 回归的简单例子是当人的

  • R语言实现线性回归的示例

    R语言实现线性回归的示例

    在统计学中,线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析. 简单对来说就是用来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法. 回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析.如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析. 一元线性回归分析法的数学方程: y = ax + b

  • R语言如何进行线性回归的拟合度详解

    R语言进行线性回归的拟合度. 本文只是使用 R做回归计算,查看拟合度等,不讨论 R 函数的内部公式 在R中线性回归分析的函数是lm(),基本语法是 一元回归: lm(y ~ x,data) 多元回归:lm(y ~ x1+x2+x3-,data) 创建关系模型并获取系数 x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131) y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48) # 使用lm()函数

  • R语言与多元线性回归分析计算案例

    R语言与多元线性回归分析计算案例

    目录 计算实例 分析 模型的进一步分析 计算实例 例 6.9 某大型牙膏制造企业为了更好地拓展产品市场,有效地管理库存,公司董事会要求销售部门根据市场调查,找出公司生产的牙膏销售量与销售价格,广告投入等之间的关系,从而预测出在不同价格和广告费用下销售量.为此,销售部门的研究人员收集了过去30个销售周期(每个销售周期为4周)公司生产的牙膏的销售量.销售价格.投入的广告费用,以及周期其他厂家生产同类牙膏的市场平均销售价格,如表6.4所示. 试根据这些数据建立一个数学模型,分析牙膏销售量与其他因素的关

  • R语言实现广义线性回归模型

    R语言实现广义线性回归模型

    目录 1 与广义线性模型有关的R函数 2 正态分布族 3 二项分布族 例  R. Norell实验 广义线性模型(GLM)是常见正态线性模型的直接推广,它可以适用于连续数据和离散数据,特别是后者,如属性数据.计数数据.这在应用上,尤其是生物.医学.经济和社会数据的统计分析上,有着重要意义. 对于广义线性模型应有一下三个概念: 第一是线性自变量,它表明第i个响应变量的期望值E(yi)只能通过线性自变量βTxi而依赖于xi,其中如通常一样,β是未知参数的(p+1)x1向量,可能包含截距. 第二是连续

  • R语言中逻辑回归知识点总结

    逻辑回归是回归模型,其中响应变量(因变量)具有诸如True / False或0/1的分类值. 它实际上基于将其与预测变量相关的数学方程测量二元响应的概率作为响应变量的值. 逻辑回归的一般数学方程为 y = 1/(1+e^-(a+b1x1+b2x2+b3x3+...)) 以下是所使用的参数的描述 y是响应变量. x是预测变量. a和b是作为数字常数的系数. 用于创建回归模型的函数是glm()函数. 语法 逻辑回归中glm()函数的基本语法是 glm(formula,data,family) 以下是

  • R语言实现随机森林的方法示例

    目录 随机森林算法介绍 算法介绍: 决策树生长步骤: 投票过程: 基本思想: 随机森林的优点: 缺点 R语言实现 随机森林模型搭建 1:randomForest()函数用于构建随机森林模型 2:importance()函数用于计算模型变量的重要性 3:MDSplot()函数用于实现随机森林的可视化 4:rfImpute()函数可为存在缺失值的数据集进行插补(随机森林法),得到最优的样本拟合值 5:treesize()函数用于计算随机森林中每棵树的节点个数 随机森林算法介绍 算法介绍: 简单的说,

  • R语言关于泊松回归知识点总结

    泊松回归(英语:Poisson regression)包括回归模型,其中响应变量是计数而不是分数的形式. 例如,足球比赛系列中的出生次数或胜利次数. 此外,响应变量的值遵循泊松分布. 泊松回归的一般数学方程为 log(y) = a + b1x1 + b2x2 + bnxn..... 以下是所使用的参数的描述 ​y​是响应变量. ​a​和​b​是数字系数. ​x​是预测变量. 用于创建泊松回归模型的函数是​glm()​函数. 语法 在泊松回归中​glm()​函数的基本语法是 glm(formula

  • 详解R语言中的多项式回归、局部回归、核平滑和平滑样条回归模型

    详解R语言中的多项式回归、局部回归、核平滑和平滑样条回归模型

    在标准线性模型中,我们假设 .当线性假设无法满足时,可以考虑使用其他方法. 多项式回归 扩展可能是假设某些多项式函数, 同样,在标准线性模型方法(使用GLM的条件正态分布)中,参数  可以使用最小二乘法获得,其中  在  . 即使此多项式模型不是真正的多项式模型,也可能仍然是一个很好的近似值 .实际上,根据 Stone-Weierstrass定理,如果  在某个区间上是连续的,则有一个统一的近似值  ,通过多项式函数. 仅作说明,请考虑以下数据集 db = data.frame(x=xr,y=y

  • 详解R语言实现前向逐步回归(前向选择模型)

    详解R语言实现前向逐步回归(前向选择模型)

    目录 前向逐步回归原理 数据导入并分组 导入数据 特征与标签分开存放 前向逐步回归构建输出特征集合 从空开始一次创建属性列表 模型效果评估 前向逐步回归原理 前向逐步回归的过程是:遍历属性的一列子集,选择使模型效果最好的那一列属性.接着寻找与其组合效果最好的第二列属性,而不是遍历所有的两列子集.以此类推,每次遍历时,子集都包含上一次遍历得到的最优子集.这样,每次遍历都会选择一个新的属性添加到特征集合中,直至特征集合中特征个数不能再增加. 数据导入并分组 导入数据,将数据集抽取70%作为训练集,剩

随机推荐