python实现感知器算法详解

在1943年，沃伦麦卡洛可与沃尔特皮茨提出了第一个脑神经元的抽象模型，简称麦卡洛可-皮茨神经元（McCullock-Pitts neuron）简称MCP，大脑神经元的结构如下图。麦卡洛可和皮茨将神经细胞描述为一个具备二进制输出的逻辑门。树突接收多个输入信号，当输入信号累加超过一定的值（阈值），就会产生一个输出信号。弗兰克罗森布拉特基于MCP神经元提出了第一个感知器学习算法，同时它还提出了一个自学习算法，此算法可以通过对输入信号和输出信号的学习，自动的获取到权重系数，通过输入信号与权重系数的乘积来判断神经元是否被激活（产生输出信号）。

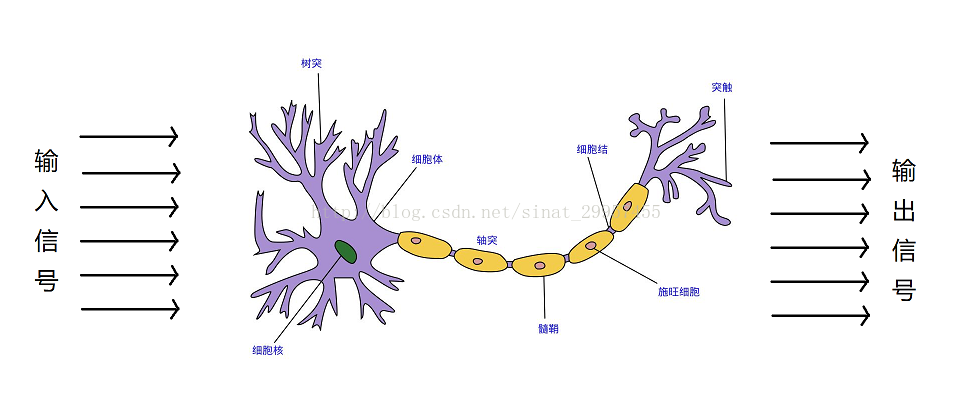
一、感知器算法

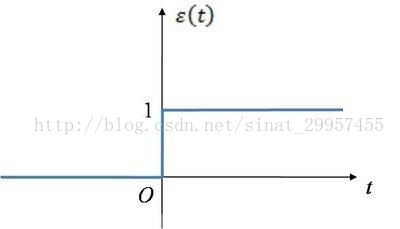
我们将输入信号定义为一个x向量，x=(x1,x2,x3..)，将权重定义为ω=(ω1,ω2,ω3...)其中ω0的值为，将z定义为为两个向量之间的乘积，所以输出z=x1*ω1 + x2*ω2+....，然后将z通过激励（激活）函数，作为真正的输出。其中激活函数是一个分段函数，下图是一个阶跃函数，当输入信号大于0的时候输出为1，小于0的时候输出为0，这里的阶跃函数阈值设置为0了。定义激活函数为Φ(z)，给激活函数Φ(z)设定一个阈值θ，当激活函数的输出大于阈值θ的时候，将输出划分为正类(1)，小于阈值θ的时候将输出划分为负类(-1)。如果，将阈值θ移到等式的左边z=x1*ω1+x2*ω2+....+θ,我们可以将θ看作为θ=x0*ω0，其中输出x0为1，ω0为-θ。将阈值θ移到等式的左边之后，就相当于激活函数的阈值由原来的θ变成了0。

感知器算法的工作过程：

1、将权重ω初始化为零或一个极小的随机数。

2、迭代所有的训练样本（已知输入和输出），执行如下操作：

a、通过权重和已知的输入计算输出

b、通过a中的输出与已知输入的输出来更新权重

权重的更新过程，如上图的公式，其中ω与x都是相对应的（当ω为ω0的时候，x为1），η为学习率介于0到1之间的常数，其中y为输入所对应的输出，后面的y（打不出来）为a中所计算出来的输出。通过迭代对权重的更新，当遇到类标预测错误的情况下，权重的值会趋于正类别和负类别的方向。

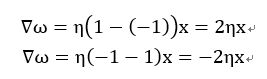
第一个公式表示的是，当真实的输出为1的情况下，而预测值为-1，所以我们就需要增加权重来使得预测值往1靠近。

第二个公式表示的是，当真实的输出为-1的情况下，而预测值为1，所以我们就需要减少权重来使得预测值往-1靠近。

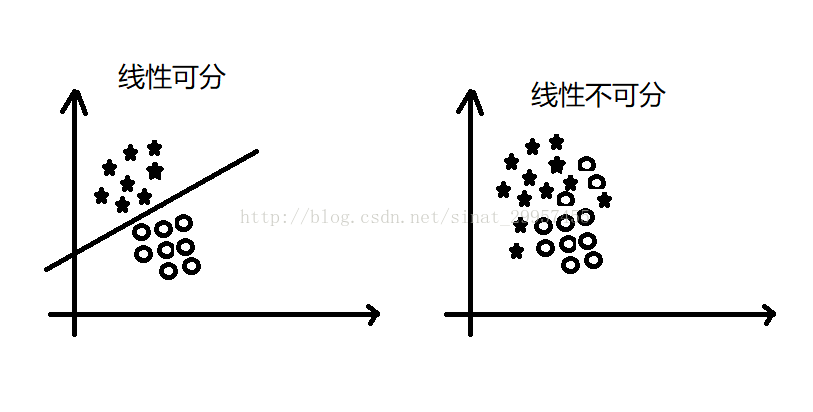
注意：感知器收敛的前提是两个类别必须是线性可分的，且学习率足够小。如果两个类别无法通过一个线性决策边界进行划分，我们可以设置一个迭代次数或者一个判断错误样本的阈值，否则感知器算法会一直运行下去。

最后，用一张图来表示感知器算法的工作过程

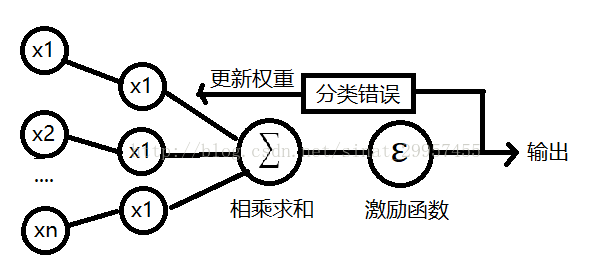
二、python实现感知器算法

import numpy as np 

class Perceptron(object):
  '''''
  输入参数：
  eta:学习率，在0~1之间,默认为0.01
  n_iter:设置迭代的次数,默认为10
  属性：
  w_:一维数组，模型的权重
  errors_:列表，被错误分类的数据
  '''
  #初始化对象
  def __init__(self,eta=0.01,n_iter=10):
    self.eta = eta
    self.n_iter = n_iter
  #根据输入的x和y训练模型
  def fit(self,x,y):
    #初始化权重
    self.w_ = np.zeros(1 + x.shape[1])
    #初始化错误列表
    self.errors_=[]
    #迭代输入数据，训练模型
    for _ in range(self.n_iter):
      errors = 0
      for xi,target in zip(x,y):
        #计算预测与实际值之间的误差在乘以学习率
        update = self.eta * (target - self.predict(xi))
        #更新权重
        self.w_[1:] += update * xi
        #更新W0
        self.w_[0] += update * 1
        #当预测值与实际值之间误差为0的时候,errors=0否则errors=1
        errors += int(update != 0)
      #将错误数据的下标加入到列表中
      self.errors_.append(errors)
    return self
  #定义感知器的传播过程
  def net_input(self,x):
    #等价于sum(i*j for i,j in zip(x,self.w_[1:])),这种方式效率要低于下面
    return np.dot(x,self.w_[1:]) + self.w_[0]
  #定义预测函数
  def predict(self,x):
    #类似于三元运算符，当self.net_input(x) >= 0.0 成立时返回1，否则返回-1
    return np.where(self.net_input(x) >= 0.0 , 1 , -1)

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。