Python实现快速傅里叶变换的方法（FFT）

本文介绍了Python实现快速傅里叶变换的方法（FFT），分享给大家，具体如下：

这里做一下记录，关于FFT就不做介绍了，直接贴上代码，有详细注释的了：

import numpy as np
from scipy.fftpack import fft,ifft
import matplotlib.pyplot as plt
import seaborn

#采样点选择1400个，因为设置的信号频率分量最高为600赫兹，根据采样定理知采样频率要大于信号频率2倍，所以这里设置采样频率为1400赫兹（即一秒内有1400个采样点，一样意思的）
x=np.linspace(0,1,1400)  

#设置需要采样的信号，频率分量有180，390和600
y=7*np.sin(2*np.pi*180*x) + 2.8*np.sin(2*np.pi*390*x)+5.1*np.sin(2*np.pi*600*x)

yy=fft(y)      #快速傅里叶变换
yreal = yy.real    # 获取实数部分
yimag = yy.imag    # 获取虚数部分

yf=abs(fft(y))    # 取绝对值
yf1=abs(fft(y))/len(x)   #归一化处理
yf2 = yf1[range(int(len(x)/2))] #由于对称性，只取一半区间

xf = np.arange(len(y))  # 频率
xf1 = xf
xf2 = xf[range(int(len(x)/2))] #取一半区间

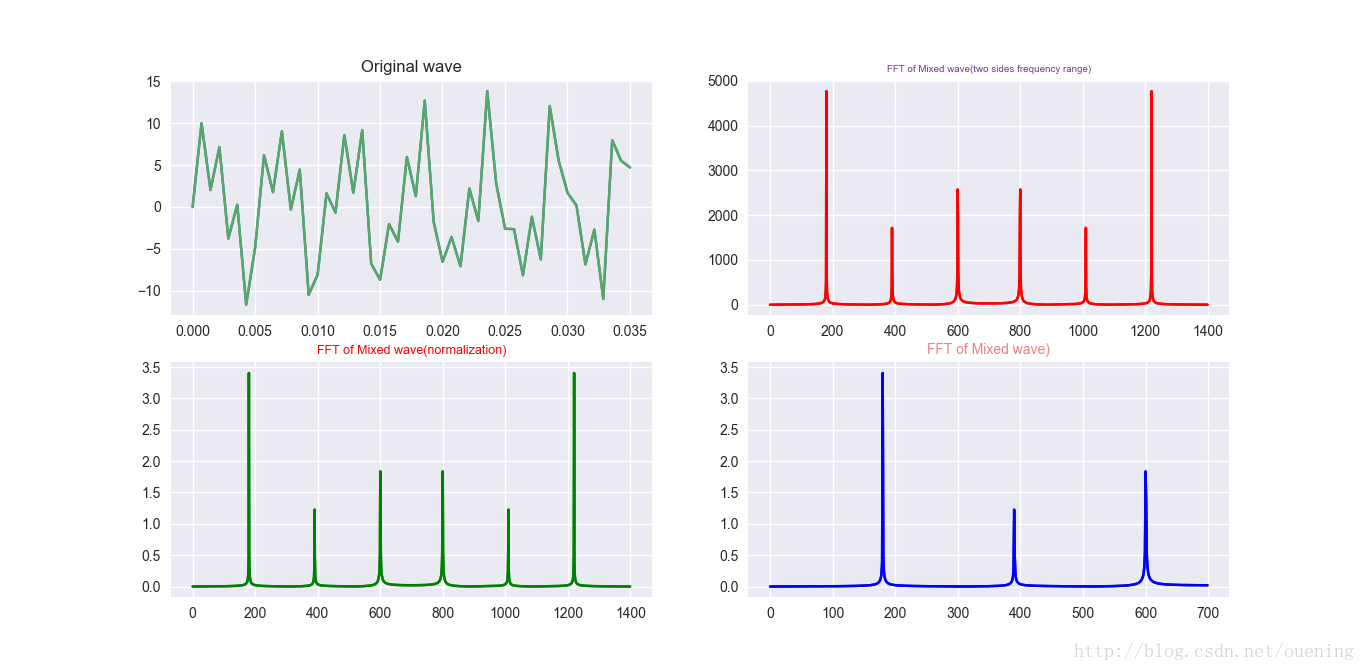
plt.subplot(221)
plt.plot(x[0:50],y[0:50])
plt.title('Original wave')

plt.subplot(222)
plt.plot(xf,yf,'r')
plt.title('FFT of Mixed wave(two sides frequency range)',fontsize=7,color='#7A378B') #注意这里的颜色可以查询颜色代码表

plt.subplot(223)
plt.plot(xf1,yf1,'g')
plt.title('FFT of Mixed wave(normalization)',fontsize=9,color='r')

plt.subplot(224)
plt.plot(xf2,yf2,'b')
plt.title('FFT of Mixed wave)',fontsize=10,color='#F08080')

plt.show()

结果：

2017/7/11更新

再添加一个简单的例子

# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
import seaborn

Fs = 150.0;     # sampling rate采样率
Ts = 1.0/Fs;    # sampling interval 采样区间
t = np.arange(0,1,Ts)  # time vector,这里Ts也是步长

ff = 25;     # frequency of the signal
y = np.sin(2*np.pi*ff*t)

n = len(y)     # length of the signal
k = np.arange(n)
T = n/Fs
frq = k/T     # two sides frequency range
frq1 = frq[range(int(n/2))] # one side frequency range

YY = np.fft.fft(y)   # 未归一化
Y = np.fft.fft(y)/n   # fft computing and normalization 归一化
Y1 = Y[range(int(n/2))]

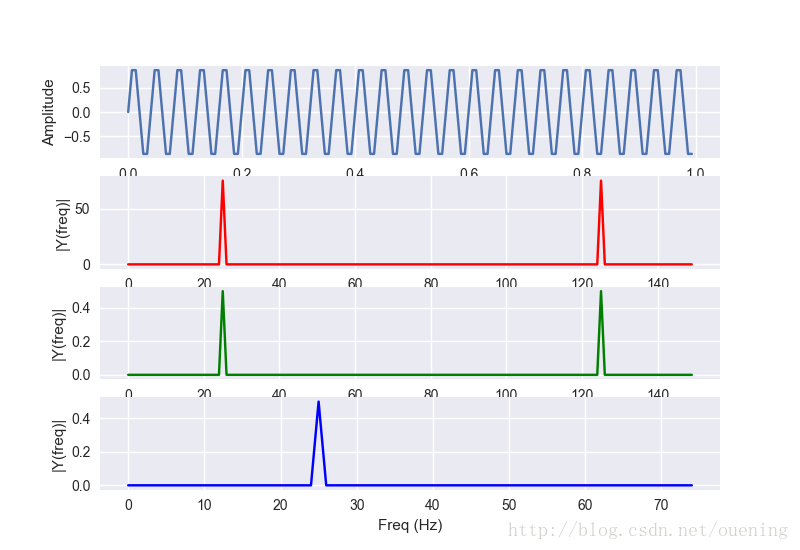
fig, ax = plt.subplots(4, 1)

ax[0].plot(t,y)
ax[0].set_xlabel('Time')
ax[0].set_ylabel('Amplitude')

ax[1].plot(frq,abs(YY),'r') # plotting the spectrum
ax[1].set_xlabel('Freq (Hz)')
ax[1].set_ylabel('|Y(freq)|')

ax[2].plot(frq,abs(Y),'G') # plotting the spectrum
ax[2].set_xlabel('Freq (Hz)')
ax[2].set_ylabel('|Y(freq)|')

ax[3].plot(frq1,abs(Y1),'B') # plotting the spectrum
ax[3].set_xlabel('Freq (Hz)')
ax[3].set_ylabel('|Y(freq)|')

plt.show()

相关文章：傅立叶级数展开初探(Python)

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。

赞 (0)

相关推荐

  • python傅里叶变换FFT绘制频谱图

    本文实例为大家分享了python傅里叶变换FFT绘制频谱图的具体代码,供大家参考,具体内容如下 频谱图的横轴表示的是 频率, 纵轴表示的是振幅 #coding=gbk import numpy as np import pandas as pd import matplotlib.pyplot as plt #依据快速傅里叶算法得到信号的频域 def test_fft(): sampling_rate = 8000 #采样率 fft_size = 8000 #FFT长度 t = np.arang

  • opencv python 傅里叶变换的使用

    理论 傅立叶变换用于分析各种滤波器的频率特性,对于图像,2D离散傅里叶变换(DFT)用于找到频域.快速傅里叶变换(FFT)的快速算法用于计算DFT. 于一个正弦信号,x(t)=Asin(2πft),我们可以说 f 是信号的频率,如果它的频率域被接受,我们可以看到 f 的峰值.如果信号被采样来形成一个离散信号,我们得到相同的频率域,但是在[−π,π] or [0,2π]范围内是周期性的 (or [0,N] for N-point DFT). 可以将图像视为在两个方向上采样的信号.因此,在X和Y方向

  • 使用python实现离散时间傅里叶变换的方法

    使用python实现离散时间傅里叶变换的方法

    我们经常使用傅里叶变换来计算数字信号的频谱,进而分析数字信号,离散时间傅里叶变换的公式为: 可是自己动手实现一遍才是最好的学习. 在数字分析里面,傅里叶变换默认等时间间隔采样,不需要时间序列,只需要信号数组即可分析. 分析过程如下: 对于含有 n 个样本值的数字信号序列,根据奈奎斯特采样定律,包含的周期数最大为 n/2,周期数为 0 代表直流分量.所以,当周期数表示为离散的 0,1,2,3-n/2 ,总的数目为 n/2+1个 傅里叶变换之后的结果为复数, 下标为 k 的复数 a+b*j 表示时域

  • FFT快速傅里叶变换的python实现过程解析

    FFT快速傅里叶变换的python实现过程解析

    FFT是DFT的高效算法,能够将时域信号转化到频域上,下面记录下一段用python实现的FFT代码. # encoding=utf-8 import numpy as np import pylab as pl # 导入和matplotlib同时安装的作图库pylab sampling_rate = 8000 # 采样频率8000Hz fft_size = 512 # 采样点512,就是说以8000Hz的速度采512个点,我们获得的数据只有这512个点的对应时刻和此时的信号值. t = np.l

  • Python中的id()函数指的什么

    Python官方文档给出的解释是 id(object) Return the "identity" of an object. This is an integer (or long integer) which is guaranteed to be unique and constant for this object during its lifetime. Two objects with non-overlapping lifetimes may have the same

  • python连接数据库的方法

    python连接数据库的方法

    MYSQL模块暂时还不支持python3.0以上的版本,由于我下载的python是3.0版本的,所以想要连接数据库只能利用其它的方法. Python3.x连接MySQL的方案有:oursql, PyMySQL, myconnpy 等,这里主要是安装pymysql 1.安装 pymysql安装:找到python文件夹pip程序的位置打开命令窗口: pip install pymysql3 2.使用 安装完毕后,数据库连接的具体步骤如下 引入 API 模块. 获取与数据库的连接. 执行SQL语句和存

  • python实现傅里叶级数展开的实现

    python实现傅里叶级数展开的实现

    傅立叶级数的介绍我就不说了,自己也是应用为主,之前一直觉得很难懂,但最近通过自己编程实现了一些函数的傅立叶级数展开之后对傅立叶 级数展开的概念比较清楚了 (1)函数如下 函数图象如下: 代码: from pylab import * x = mgrid[-10:10:0.02] # 这里类似于MATLAB用冒号产生步长为0.02的序列,但是语法和MATLAB不同 n = arange(1,1000) def fourier_transform(): a0 = (1-exp(-pi))/pi+1

  • Python实现快速傅里叶变换的方法（FFT）

    本文介绍了Python实现快速傅里叶变换的方法(FFT),分享给大家,具体如下: 这里做一下记录,关于FFT就不做介绍了,直接贴上代码,有详细注释的了: import numpy as np from scipy.fftpack import fft,ifft import matplotlib.pyplot as plt import seaborn #采样点选择1400个,因为设置的信号频率分量最高为600赫兹,根据采样定理知采样频率要大于信号频率2倍,所以这里设置采样频率为1400赫兹(即

  • Python实现快速多线程ping的方法

    本文实例讲述了Python实现快速多线程ping的方法.分享给大家供大家参考.具体如下: #!/usr/bin/python #_*_coding:utf-8_*_ # ''' 名称:快速多线程ping程序 开发:gyhong gyh9711 日期:20:51 2011-04-25 ''' import pexpect import datetime from threading import Thread host=["192.168.1.1","192.168.1.123

  • Python如何快速上手? 快速掌握一门新语言的方法

    那么Python如何快速上手?找来了一篇广受好评的新语言学习方法介绍,供大家参考. 听说,你决定要为你的 "技能树" 再添加一门特定的编程语言.那该怎么办呢? 在这篇文章中,作者提出了 12 项关于学习技术的建议.记住每个人学习的方式都不一样.其中一些可能对你十分有用,而其他的则可能无法满足你的需求.如果你开始担心一个策略,请尝试另一个策略并看看它哪里适合你. 1. 将其与类似的语言进行比较.当你首次观看有关该语言的第一个教程或阅读代码时,请尝试猜测该语言的每个部分将会做什么,并检查你

  • python字典快速保存于读取的方法

    在使用python编程过程中,我们往往需要借助字典来提高编程效率.同时为了调试方便,我们希望将某些变量保存为中间文件. 例如,在协同过滤算法中,相似性的训练结果可以保存为中间文件,方便调试.python对字典的保存与读取可以借助于json方便的实现. #保存 dict_name = {1:{1:2,3:4},2:{3:4,4:5}} f = open('temp.txt','w') f.write(str(dict_name)) f.close() #读取 f = open('temp.txt'

  • transform python环境快速配置方法

    经常在数据开发中需要搞udf,最近发现transform更加方便易用,但是经常会涉及到集群python版本不一.包不全或者部分机器上没有安装python. 所以咱们需要快速的进行环境配置. 因为mac自带安装好的python,所以就不讲怎么安装了.可以去官网下个: https://www.python.org/downloads/source/ 1.安装虚拟环境工具: 执行:pip install virtualenv,如果没有pip的话可以google一把,自行安装 2.创建虚拟环境: 新建一

  • python实现快速文件格式批量转换的方法

    用python实现文件夹下的成批文件格式转换 我们对于文件转换的需求很大,甚至于对于图片的格式,JPG和PNG格式在肉眼看来都没什么差别,但是对于计算机而言,它有时候就只接受这些肉眼看起来差不多的格式的其中一种. 环境 windows10 python3.7+pycharm 创建目录 1.在编程前,创建一个文件夹,并放入你想用的文件(非目录),这些文件的格式不合适. 例如,我在桌面创建了名为"in_path"的文件夹,在里面放进了.pgm和.png格式的文件,想让他们都转化成.jpg格

  • Python编程快速上手——疯狂填词程序实现方法分析

    本文实例讲述了Python疯狂填词程序实现方法.分享给大家供大家参考,具体如下: 题目如下: 创建一个疯狂填词程序,它将读入文件,并让用户在该文本文件中出现ADJECTIVE,NOUN,ADVERB,VERB等单词的地方,加上它们自己的文本. 例如源文本如下: The ADJECTIVE panda walked to the NOUN and then VERB. A nearby NOUN was unaffected by these events. 程序将找到这些出现的单词,提示用户取代

  • python字符类型的一些方法小结

    int 数字类型 class int(object): """ int(x=0) -> int or long int(x, base=10) -> int or long Convert a number or string to an integer, or return 0 if no arguments are given. If x is floating point, the conversion truncates towards zero. If

  • python 如何快速找出两个电子表中数据的差异

    最近刚接触python,找点小任务来练练手,希望自己在实践中不断的锻炼自己解决问题的能力. 公司里会有这样的场景:有一张电子表格的内容由两三个部门或者更多的部门用到,这些员工会在维护这些表格中不定期的跟新一些自己部门的数据,时间久了,大家的数据就开始打架了,非常不利于管理.怎样快速找到两个或者多个电子表格中数据的差异呢? 解决办法: 1. Excel自带的方法(有兴趣的自行百度) 2. python 写一个小脚本 #!/usr/bin/env python # -*- coding: utf-8

随机推荐