算法系列15天速成 第一天 七大经典排序【上】

针对现实中的排序问题，算法有七把利剑可以助你马道成功。

首先排序分为四种：
      交换排序： 包括冒泡排序，快速排序。
      选择排序： 包括直接选择排序，堆排序。
      插入排序： 包括直接插入排序，希尔排序。
      合并排序： 合并排序。

那么今天我们讲的就是交换排序，我们都知道，C#类库提供的排序是快排，为了让今天玩的有意思点，
我们设计算法来跟类库提供的快排较量较量。争取KO对手。

冒泡排序：

首先我们自己来设计一下“冒泡排序”，这种排序很现实的例子就是：
我抓一把沙仍进水里，那么沙子会立马沉入水底， 沙子上的灰尘会因为惯性暂时沉入水底，但是又会立马像气泡一样浮出水面，最后也就真相大白咯。

关于冒泡的思想，我不会说那么官方的理论，也不会贴那些文字上来，我的思想就是看图说话。

那么我们就上图.

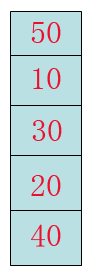
要达到冒泡的效果，我们就要把一组数字竖起来看，大家想想，如何冒泡？如何来体会重的沉底，轻的上浮？

第一步:  我们拿40跟20比，发现40是老大，不用交换。
第二步:  然后向前推一步，就是拿20跟30比，发现30是老大，就要交换了。
第三步：拿交换后的20跟10比，发现自己是老大，不用交换。
第四步：拿10跟50交换，发现50是老大，进行交换。

最后，我们经过一次遍历，把数组中最小的数字送上去了，看看，我们向目标又迈进了一步。

现在大家思想都知道了，下面我们就强烈要求跟快排较量一下，不是你死就是我活。

代码如下:

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Diagnostics;
using System.Threading;

namespace BubbleSort
{
    public class Program
    {
        static void Main(string[] args)
        {
            //五次比较
            for (int i = 1; i <= 5; i++)
            {
                List<int> list = new List<int>();
                //插入2k个随机数到数组中
                for (int j = 0; j < 2000; j++)
                {
                    Thread.Sleep(1);
                    list.Add(new Random((int)DateTime.Now.Ticks).Next(0, 100000));
                }
                Console.WriteLine("\n第" + i + "次比较：");
                Stopwatch watch = new Stopwatch();
                watch.Start();
                var result = list.OrderBy(single => single).ToList();
                watch.Stop();
                Console.WriteLine("\n快速排序耗费时间：" + watch.ElapsedMilliseconds);
                Console.WriteLine("输出前是十个数:" + string.Join(",", result.Take(10).ToList()));
                watch.Start();
                result = BubbleSort(list);
                watch.Stop();
                Console.WriteLine("\n冒泡排序耗费时间：" + watch.ElapsedMilliseconds);
                Console.WriteLine("输出前是十个数:" + string.Join(",", result.Take(10).ToList()));
            }
        }

//冒泡排序算法
        static List<int> BubbleSort(List<int> list)
        {
            int temp;
            //第一层循环： 表明要比较的次数，比如list.count个数，肯定要比较count-1次
            for (int i = 0; i < list.Count - 1; i++)
            {
                //list.count-1：取数据最后一个数下标，
//j>i: 从后往前的的下标一定大于从前往后的下标，否则就超越了。
                for (int j = list.Count - 1; j > i; j--)
                {
                    //如果前面一个数大于后面一个数则交换
                    if (list[j - 1] > list[j])
                    {
                        temp = list[j - 1];
                        list[j - 1] = list[j];
                        list[j] = temp;
                    }
                }
            }
            return list;
        }
    }
}

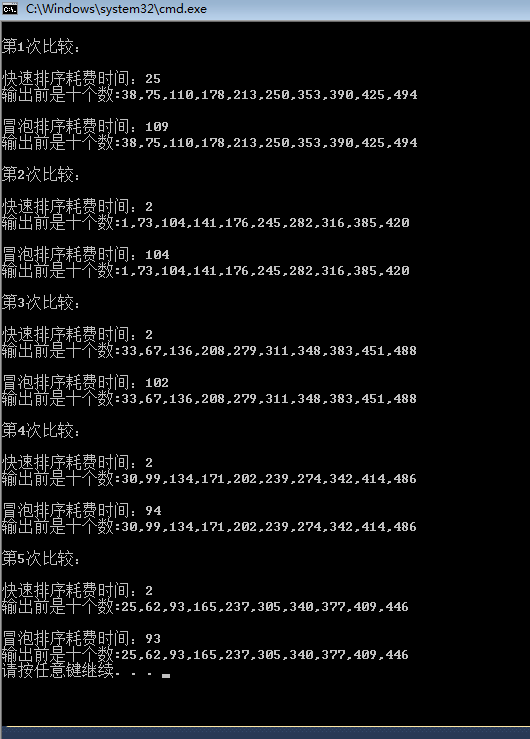
呜呜，看着这两种排序体检报告，心都凉了，冒泡被快排KO了，真惨，难怪人家说冒泡效率低，原来真tmd低。

快速排序：

既然能把冒泡KO掉，马上就激起我们的兴趣，tnd快排咋这么快，一定要好好研究一下。

首先上图：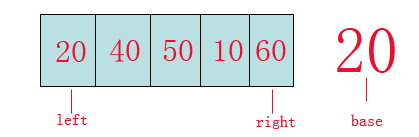    

从图中我们可以看到：

left指针，right指针，base参照数。

其实思想是蛮简单的，就是通过第一遍的遍历（让left和right指针重合）来找到数组的切割点。

第一步：首先我们从数组的left位置取出该数（20）作为基准（base）参照物。
第二步：从数组的right位置向前找，一直找到比（base）小的数，
            如果找到，将此数赋给left位置（也就是将10赋给20），
            此时数组为：10，40，50，10，60，
            left和right指针分别为前后的10。
第三步：从数组的left位置向后找，一直找到比（base）大的数，
             如果找到，将此数赋给right的位置（也就是40赋给10），
             此时数组为：10，40，50，40，60，
             left和right指针分别为前后的40。
第四步：重复“第二,第三“步骤，直到left和right指针重合，
             最后将（base）插入到40的位置，
             此时数组值为： 10，20，50，40，60，至此完成一次排序。
第五步：此时20已经潜入到数组的内部，20的左侧一组数都比20小，20的右侧作为一组数都比20大，
            以20为切入点对左右两边数按照"第一，第二，第三，第四"步骤进行，最终快排大功告成。

同样，我们把自己设计的快排跟类库提供的快拍比较一下。看谁牛X。

代码如下:

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading;
using System.Diagnostics;

namespace QuickSort
{
    public class Program
    {
        static void Main(string[] args)
        {
            //5次比较
            for (int i = 1; i <= 5; i++)
            {
                List<int> list = new List<int>();

//插入200个随机数到数组中
                for (int j = 0; j < 200; j++)
                {
                    Thread.Sleep(1);
                    list.Add(new Random((int)DateTime.Now.Ticks).Next(0, 10000));
                }

Console.WriteLine("\n第" + i + "次比较：");

Stopwatch watch = new Stopwatch();

watch.Start();
                var result = list.OrderBy(single => single).ToList();
                watch.Stop();

Console.WriteLine("\n系统定义的快速排序耗费时间：" + watch.ElapsedMilliseconds);
                Console.WriteLine("输出前是十个数:" + string.Join(",", result.Take(10).ToList()));

watch.Start();
                new QuickSortClass().QuickSort(list, 0, list.Count - 1);
                watch.Stop();

Console.WriteLine("\n俺自己写的快速排序耗费时间：" + watch.ElapsedMilliseconds);
                Console.WriteLine("输出前是十个数:" + string.Join(",", list.Take(10).ToList()));

}
        }
    }

public class QuickSortClass
    {

///<summary>
/// 分割函数
///</summary>
///<param name="list">待排序的数组</param>
///<param name="left">数组的左下标</param>
///<param name="right"></param>
///<returns></returns>
        public int Division(List<int> list, int left, int right)
        {
            //首先挑选一个基准元素
            int baseNum = list[left];

while (left < right)
            {
                //从数组的右端开始向前找，一直找到比base小的数字为止(包括base同等数)
                while (left < right && list[right] >= baseNum)
                    right = right - 1;

//最终找到了比baseNum小的元素，要做的事情就是此元素放到base的位置
                list[left] = list[right];

//从数组的左端开始向后找，一直找到比base大的数字为止（包括base同等数）
                while (left < right && list[left] <= baseNum)
                    left = left + 1;

//最终找到了比baseNum大的元素，要做的事情就是将此元素放到最后的位置
                list[right] = list[left];
            }
            //最后就是把baseNum放到该left的位置
            list[left] = baseNum;

//最终，我们发现left位置的左侧数值部分比left小，left位置右侧数值比left大
//至此，我们完成了第一篇排序
            return left;
        }

public void QuickSort(List<int> list, int left, int right)
        {
            //左下标一定小于右下标，否则就超越了
            if (left < right)
            {
                //对数组进行分割，取出下次分割的基准标号
                int i = Division(list, left, right);

//对“基准标号“左侧的一组数值进行递归的切割，以至于将这些数值完整的排序
                QuickSort(list, left, i - 1);

//对“基准标号“右侧的一组数值进行递归的切割，以至于将这些数值完整的排序
                QuickSort(list, i + 1, right);
            }
        }
    }
}

不错，快排就是快，难怪内库非要用他来作为排序的标准。

嗯，最后要分享下：

冒泡的时间复杂度为： 0(n) - 0(n^2)
快排的时间复杂度为:

平均复杂度： N(logN)
    最坏复杂度：  0(n^2)