C语言数据结构与算法之时间空间复杂度入门

2024-12-13 18:04:16

数据结构与算法

终于开始搞这块难啃的骨头了，走上这条漫漫长路之前要明白：

什么是数据结构？什么是算法？

是数据之间存在一种或多种特定关系的数据元素集合，为编写出一个“好”的程序，必须分析待处理对象的特性及各处理对象之间存在的关系，这也就是研究数据结构的意义所在为编写出一个“好”的程序，必须分析待处理对象的特性及各处理对象之间存在的关系这也就是研究数据结构的意义所在

算法是解决特定问题求解步骤的描述，在计算机中表现为指令的有限序列，并且每条指令表示一个或多个操作

抛开上面的学术性口水话，简单来说就是:

1.数据结构是计算机存储，组织数据的方式

2.算法是一系列规定的计算步骤，为了实现的特定的计算目的而应用

给个更直观的视图就是：算法+数据结构就等于程序，数据结构可以理解为实现一个程序的基本单位，算法可以看作一个加工过程。

比如我去从一个很大的数组里面提取某个特定的对象，我们既可以老老实实从头到尾遍历查找，也就是所谓的暴力搜索，工程量随着数组的容量增大而增大；我们也可以巧夺智取，用二分查找让我们工作事半功倍。

分析维度

在知道基本概念后，我们说在拿到一个算法后，我们怎么去看他的好坏？或者给你多个算法，他们都实现同一个功能，我们怎么去判断他的优缺点去取舍呢？正常情况下，我们会选择把这个代码放在某个环境下运行比较时间，但这个做法有一个致命的缺点，在我们不同机器上，会有不同的结果，在好的机器上，运行时间会很短，但是在比较差一点的主机上，就稍有逊色，这样一来就有失公平。

大O的渐进表示法

不要直接计算时间，，我们需要去计算一个渐进的时间复杂度，也就是所谓的Big O （大O表示法），他其实本质上实在求一个量级（时间）在增加时的一个变化趋势

时间复杂度公式：T（n）=O(f(n))

T（n）：时间频度（执行次数）
n ：问题规模；
f（n）：T(n)的同数量级函数；
O ：代表正比例关系；
Ｏ(f(n)）：即算法的渐进时间复杂度

常数阶

我们的算加法的完整过程：

int main()
{
int a = 1;
int b = 1;
int sum = a+b;
printf("%d",sum);
}

我们每走一步就会执行一次，上面的代码我就执行了四次；那么如果我把他的sum部分重复执行数十次数百次数千次，但他本质上和执行四次没有区别，执行时间是恒定的，这个层面上，他的时间复杂度就是O（1）（常数阶）。

不管这个常数是多少，4或∞，都不能写成O(4)、O(∞)，都要写成O(1)

线性阶

我们给出一个 for loop

for(int a = 1;a<=n;a++)
{
 a++;
}

分析线性阶时会比常数阶更复杂因为要分析他的循环结构，上面的代码限制再++，总共执行3次，包括常数阶的赋值就是O（3n+1），在我的n足够大时他会无限接近于无穷，这时的+1就会没有意义。

这时就顺理成章，嵌套循环我们也就可以理解了，两层 for 就是O（n2)，三层就是O（n2）for 下面加一个双层for循环就是O（n+n2）……这里面就包含了**平方阶**；此时我O(n)的效率就比O（n2）高。

对数阶

我们再给出一个while loop

int n = 0;
while(n<100000)
{
n*=2;
}

我们要看执行次数就要看多少步才能走出循环，就意味着要乘 x 个2能>=10000，则表示为 2^x =100000，假设为随机数 a，则 x= log 2 ^a，
复杂度为O（logn）

除了上面三种之外还有其他的复杂度

从常数阶到阶乘是越来越复杂，我们看一下直观数据：

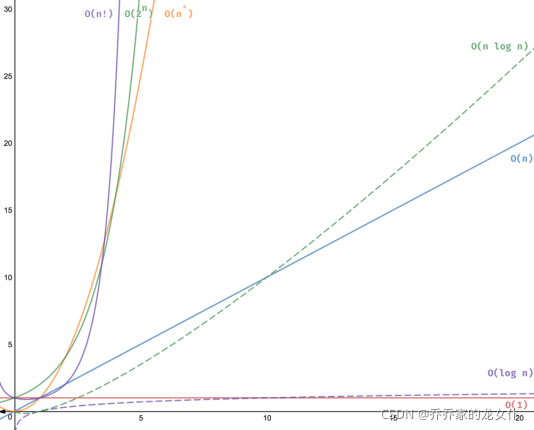
这里横轴是输入（input）量级，纵轴是消耗时间也就是时间复杂度，也就是有个很直观的信息：算法复杂度越高，需要的时间越长，到后面就直接指数级增长。

其他时间复杂度指标

虽然有下面这些种吧，但我们主要会把重心放在 O 上，毕竟它是最常用的指标。

空间复杂度

空间复杂度是指内存空间增长的趋势，相对就容易理解一些，O（1）就是相当于单次赋值，而 O（n）相当于赋值n次，可以把他想成一个大小为 n 的数组，复杂度越高需要分配的空间就越多；同理，O（n^2）就可以想成一个n行n列的二维数组。

今天就到这里吧，摸了家人们，更多关于C语言数据结构与算法时间空间复杂度的资料请关注我们其它相关文章！

C语言数据结构与算法时间空间复杂度基础实践

目录小感想时间复杂度空间复杂度小感想今天去看了看许多人今年去各个大厂面试的面经,确实如大体所说,各大公司越来越注重性能迭代,时代需要数据结构与算法这样的考试. 一个公司的成本主要来自于人力成本,但是上了规模写核心代码的人少了,成本就会来自于机器,资源,时间,抢占到这些就相当于无时无刻在减少客户流失.所以同样一段代码给两个人写,甲拿 8000,乙拿 25000,但是后者效率提高了50%,而这50%带来的收益远远超过了(25000-8000),这就是为什么许多大厂要给出如此吸引人的高薪资来
用C语言举例讲解数据结构中的算法复杂度结与顺序表

数据结构算法复杂度 1.影响算法效率的主要因素 (1)算法采用的策略和方法: (2)问题的输入规模: (3)编译器所产生的代码: (4)计算机执行速度. 2.时间复杂度 // 时间复杂度:2n + 5 long sum1(int n) { long ret = 0; \\1 int* array = (int*)malloc(n * sizeof(int)); \\1 int i = 0; \\1 for(i=0; i<n; i++) \\n { array[i] = i + 1; } for(
C语言简单实现快速排序

快速排序是一种不稳定排序,它的时间复杂度为O(n·lgn),最坏情况为O(n2):空间复杂度为O(n·lgn). 这种排序方式是对于冒泡排序的一种改进,它采用分治模式,将一趟排序的数据分割成独立的两部分,其中一组数据的每个值都小于另一组.每一趟在进行分类的同时实现排序. 其中每一趟的模式通过设置key当基准元素,key的选择可以是数据的第一个,也可以是数据的最后一个.这里以每次选取数据的第一个为例: 具体代码实现: #include<stdio.h> #define N 6 int fun(i
C语言数据结构时间复杂度及空间复杂度简要分析

目录一.时间复杂度和空间复杂度是什么? 1.1算法效率定义 1.2时间复杂度概念 1.3空间复杂度概念二.如何计算常见算法的时间复杂度和空间复杂度 2.1时间复杂度计算 2.2空间复杂度计算 2.3快速推倒大O渐进表达法三.一些特殊的情况总结一.时间复杂度和空间复杂度是什么? 1.1算法效率定义算法效率分为两种,一种是时间效率--时间复杂度,另一种是空间效率--空间复杂度 1.2时间复杂度概念时间复杂度,简言之就是你写一个代码,它解决一个问题上需要走多少步骤,需要花费多长时间.打个
C语言关于时间复杂度详解

目录一.时间复杂度 1.什么是时间复杂度? 2.如何计算? 3.常见的时间复杂度: 二.空间复杂度 1.什么是空间复杂度? 2.如何计算? 总结一.时间复杂度 1.什么是时间复杂度? 空间效率,时间效率(较为关注) 时间复杂度:算法中的操作执行次数,为算法的时间复杂度.(不是具体时间,而是执行次数) 2.如何计算? 时间复杂度 (1)是一个估算,看表达式中影响大的那一项,如N*N+2N+10中,N*N对整个式子影响最大,故其时间复杂度为N*N,用大O的渐近表示法O(N*N). (2)去掉时间
C语言数据结构与算法之时间空间复杂度入门

目录数据结构与算法什么是数据结构?什么是算法? 分析维度大O的渐进表示法常数阶线性阶对数阶其他时间复杂度指标空间复杂度数据结构与算法终于开始搞这块难啃的骨头了,走上这条漫漫长路之前要明白: 什么是数据结构?什么是算法? 是数据之间存在一种或多种特定关系的数据元素集合,为编写出一个“好”的程序,必须分析待处理对象的特性及各处理对象之间存在的关系,这也就是研究数据结构的意义所在为编写出一个“好”的程序,必须分析待处理对象的特性及各处理对象之间存在的关系这也就是研究数据结构的意义所
C语言数据结构之算法的时间复杂度

目录 1.算法的复杂度 2.时间复杂度 2.1 时间复杂度的定义 2.2 大O的渐进表示法 3.常见时间复杂度计算举例 3.1 冒泡排序的时间复杂度 3.2 二分查找的时间复杂度 3.3 阶乘(递归)的时间复杂度 3.4菲波那切数列的时间复杂度 1.算法的复杂度算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 .因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度. 时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的
C语言数据结构与算法之链表(一)

目录引言链表的相关思考链表结点结构建立链表实现插入操作完整代码引言在存储一大波数的时候,我们通常使用的是数组,但是数组有时候又会显得不够灵活,比如下面这个例子: 有一串已经排序好的数 2,3,5,8,9 ,10 如果我们想要往数组中插入6 这个元素,需要把 8 以后的元素全部往后挪一位这样操作显然很耗费时间,如果使用链表的话则会快很多.那么什么是链表呢?请看下图: 此时如果需要在8前面加入一个6,那么只需要向下图一样更改一下就可以了,而不用向像最开始那样把每个数向后挪. 链表的
C语言数据结构与算法之排序总结(二)

目录一.前言二.选择类排序 1.简单选择排序 2.树形选择排序 3.堆选择排序三.归并排序四.分配类排序 1.多关键字排序 2.链式基数排序五.总结归纳一.前言之前的排序总结(一)对插入类和交换类排序作了比较详细的总结,对于直接插入.希尔排序.冒泡排序.快速排序要求熟练掌握这篇排序全面总结(二)主要介绍选择类排序中的简单.树形和堆排序,归并排序.分配类排序的基数排序二.选择类排序选择类:每次从待排序的无序序列中,选择一个最大或最小的数字,放到前面,数据元素为空时排序结束 1.
C语言数据结构与算法之排序总结(一)

目录一.前言二.基本概念 1.排序 2.排序方法的稳定性 3.内部和外部排序三.插入类排序 1.直接插入排序 2.折半插入排序 3.希尔排序四.交换类排序 1.冒泡排序 2.快速排序五.总结比较一.前言学习目标: 排序和查找密不可分,将待处理的数据按关键值大小有序排列后,查找更加快速准确理解各种排序算法的定义和特点,并能将代码灵活运用掌握各种排序方法时间复杂度与空间复杂度理解排序稳定和不稳定的概念重点和难点: 希尔.快速.堆.归并排序这几种快
C语言数据结构与算法之图的遍历(二)

目录前言广度优先搜索过程主要思想代码实现前言在上一章的内容中我们使用了深度优先搜索来进行遍历,这一章我们选择使用广度优先搜索来完成这个图的遍历 --> 结果如下: 广度优先搜索过程使用广度优先搜索来遍历这个图的过程如下. 首先以一个未被访问过的顶点作为起始顶点,比如以1号点作为起始顶点. 将1号点放到队列中,然后将与1号点相邻的未访问过的顶点即 2,3,5号顶点依次放入队列中,如下图: 接下来将2号顶点相邻的未访问过的顶点4号放入到队列中.到此所有的顶点都访问过了,遍历
C语言数据结构与算法之图的遍历

目录引入深度优先搜索代码实现完整代码引入在数据结构中常见的有深度优先搜索和广度优先搜索.为什么叫深度和广度呢?其实是针对图的遍历而言的,请看下面这个图: 图是由一些小圆点(称为顶点) 和连接这些点的直线 (称为边)组成的. 例如上图就是由5个顶点(编号为 1,2,3,4,5) 和5条边(1-2,1-3,1-4,2-4)组成. 现在我们从1号顶点开始遍历这个图,遍历就是把图的每一个顶点都访问一次.使用深度优先搜索将会得到如下的结果. 图中每个顶点旁边的数表示这个顶点是第几个
C语言数据结构与算法之链表(二)

目录引入模拟链表介绍插入代码实现代码实现引入在上一节的学习中我们介绍了C语言如何实现链表,但是,在这一章,我们将抛开令人头秃的指针和结构体,我们将另外使用一种数组来实现的方式,叫做模拟链表.让我们一起来看看. 模拟链表介绍链表中的每一个结点都只有两个部分. 我们可以使用一个数组date来储存每序列中的每一个数.那每一个数右边的数是谁,这一点该如何解决呢?在上一章的内容中我们是使用指针来解决的,这里我们只需再用一个数组right来存放序列中每一个数右边的数是谁就可以了.具体要怎么
C语言数据结构与算法之单链表

目录基本概念读取数据元素获取第i个结点的数据元素插入数据元素初始化链表打印链表顺序表查空顺序表的删除删除第i个结点及其数据元素情况1:当删除的是第一个元素情况2:除第一个结点外完整代码删除单链表整表单链表VS顺序表基本概念链表的每一个结点中只包含一个指针域优点 : 储存空间利用高效举例来说: typedef struct student{ int id; //学生编号 char* name; //学生名称 //指向下一结点的指针 struct Studen