Java 实现一个汉诺塔实战练习

汉诺塔简介：

我们想要实现的是 让 A柱上的盘子，移动到C柱上

1层汉诺塔

2层汉诺塔

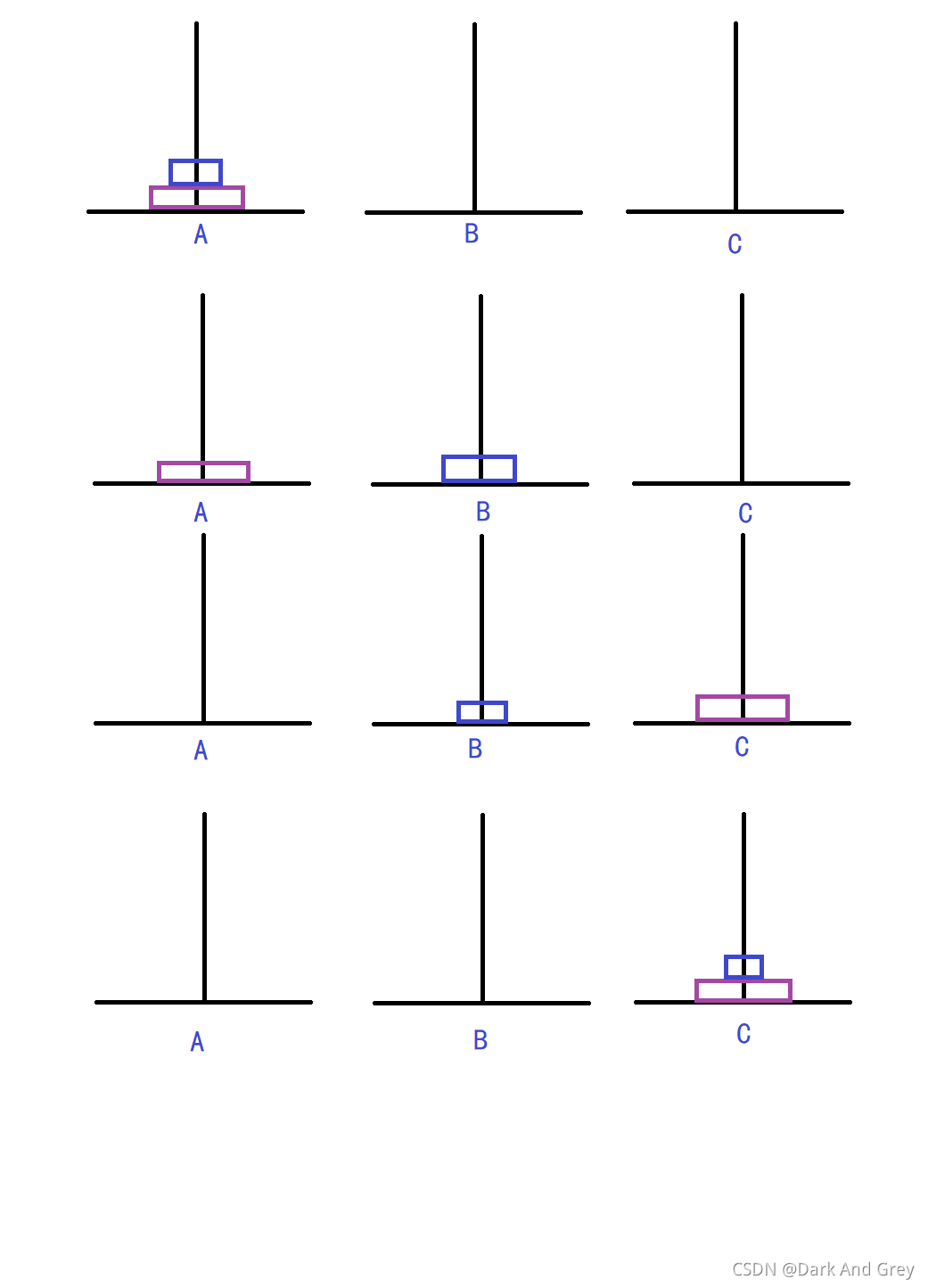
3层汉诺塔详解图

第一步

第二步

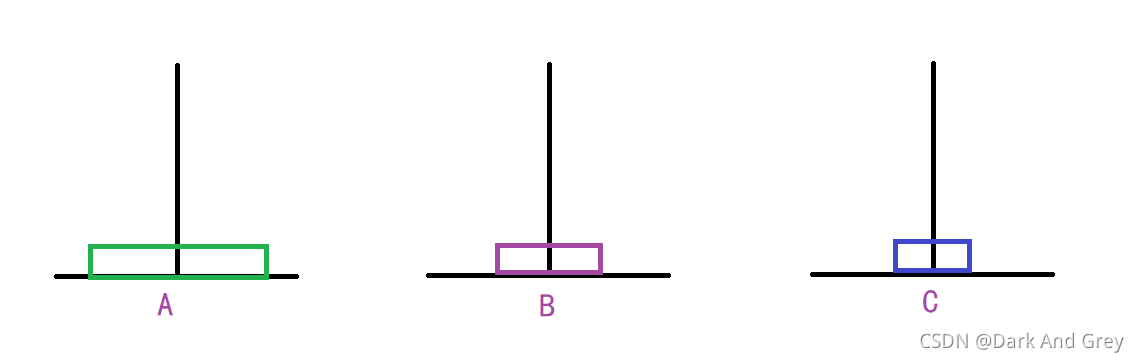
第三步

第四步

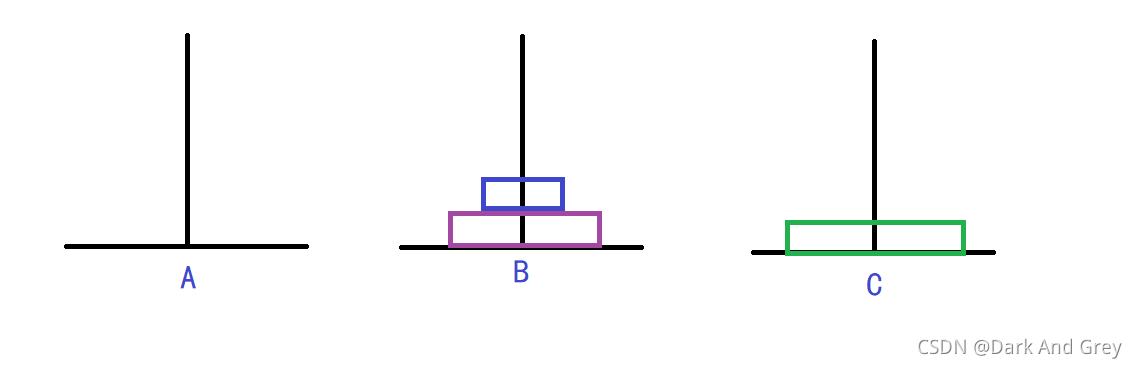
第五步

第六步

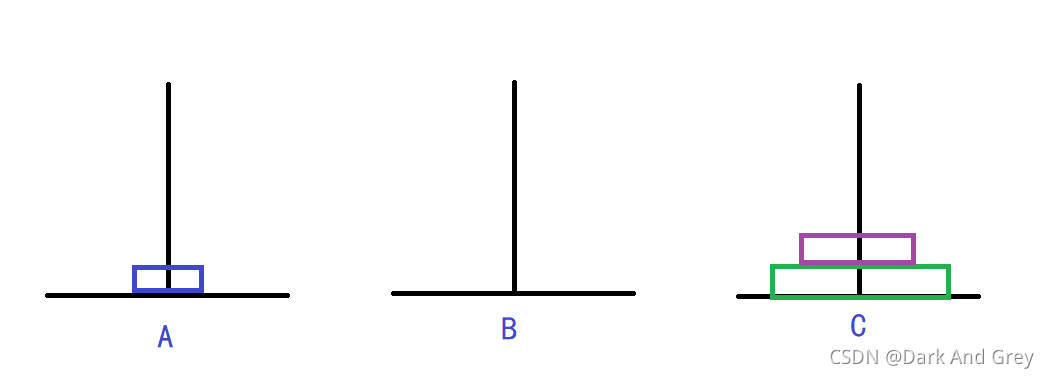
第七步

经过上面的图解，相比大家一定在一定程度了解到汉诺塔的游戏规则，以及怎么去玩。

总之 最终C柱上第一个盘子，是最大，最顶的是最小的，而且在操作过程中，前几步就是为了让三个柱子中最大的盘子移动到C柱上，
然后不断，将它两个柱子中最大盘子往上累加，（盘子从大到小，从下往上摆放）

而且盘子一多，你就会发现过程中间，除了最大的盘子，其余的盘子都会集中在 B柱上，这样才能把 A 柱上最底下也是最大的盘子，移动到C上。
这是规律一

还有一个规律，在最大的盘子移动C柱上之后，第二个大的盘子要放在A柱上，其余盘子按照规则全部放在B柱上，
这样第二大的盘子才能移动到最大的盘子上

说白了，盘子再多，也要按照上面两个规律，才能完成整个游戏

那我把最大盘子上面的所有盘子看成一个整体，放在B柱上，最大盘子移动到C柱上，把B柱上盘子直接盖上去，不就行了，反正也就是重复那两个规律而已

程序如下

import java.util.Scanner;

public class Manuscript {
    static int times;// 移动次数
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        char A = 'A';
        char B = 'B';
        char C = 'C';
        int n = scanner.nextInt();
        game(n,A,B,C);
        scanner.close();
    }
    public static void move(int disk,char M,char N){
        System.out.println("第"+(++times)+"次移动，盘子"+disk+" "+M +"---->"+N);

    }
    public static void game(int n,char A,char B,char C){
        if(n==1){
            move(n,A,C);// 把A柱目前最大盘子放在C柱上，第一次肯定最大的那个
        }else{
            // 将 n-1 个 盘子 放到B柱子，注意ABC位置，再看看下面  move(n,A,C);，细细琢磨
            game(n-1,A,C,B);// A   B(C)  C(B)

            move(n,A,C);

            // 把n-1 个盘子 放在C上，注意ACB位置
            game(n-1,B,A,C);// A(B)  B(A) C
        }
    }
}

3层汉诺塔的输出结果附图（可以返回去看看，对一对）

有什么疑问，可以在下方讨论，切记 不要自己带入一个特别大数字去展开，带入一个 1 ~3 ，了解规律就行。不主张展开，主张掌握规律（递推公式）。

本文结束。

以上就是Java 实现一个汉诺塔实战练习的详细内容，更多关于Java 汉诺塔的资料请关注我们其它相关文章！

赞 (0)

相关推荐

  • java基于递归算法实现汉诺塔问题实例

    本文实例讲述了java基于递归算法实现汉诺塔问题.分享给大家供大家参考,具体如下: package test; import java.util.List; import java.util.ArrayList; import java.util.Scanner; import sun.net.www.content.audio.x_aiff; /** * @author 年浩 * */ public class test { public static void move(char x,cha

  • Java手把手必会的实例汉诺塔讲解练习

    Java手把手必会的实例汉诺塔讲解练习

    最适合菜鸟的汉诺塔讲解 问题引入 汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘.大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上.并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘. 让我们先从小事入手. 标记汉诺塔的三根柱子分别为 a ,b ,c 标记汉诺塔上的圆盘分别为:1 ,2,3,4 -n a 柱上面只有一个圆盘时 只有这一种走法 a柱上有两个圆盘时

  • 手把手带你用java搞定汉诺塔

    手把手带你用java搞定汉诺塔

    目录 什么是汉诺塔 问题剖析 n=1 n=2 n=3 小结 Java代码实现 代码讲解 move函数 hanoiTower函数 附:C语言实现汉诺塔 总结 什么是汉诺塔 汉诺塔问题是一个经典的问题.汉诺塔(Hanoi Tower),又称河内塔,源于印度一个古老传说. 大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘. 大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上.并且规定,任何时候,在小圆盘上都不能放大圆盘,且在三根柱子之间一次只能移

  • java 汉诺塔详解及实现代码

    java 汉诺塔详解及实现代码

    java 汉诺塔详解及实现代码 实现效果图 打印的方法在 moveTheTopOne() 方法中被调用,调用该方法前打印出移动的方向--从X号塔往Y号塔 汉诺塔要求:将第一座塔上的所有盘子,借助第二座塔,全部搬运到第三座塔上. 规则:一次只能搬运一个盘子,不准将大盘子落在小盘子上.  汉诺塔实现代码: public class NewHanoi { public static int tiers = 4; // tiers 层数 private static List<String> pago

  • Java编程用栈来求解汉诺塔问题的代码实例（非递归）

    [题目] 汉诺塔问题比较经典,这里修改一下游戏规则:现在限制不能从最左侧的塔直接移动到最右侧,也不能从最右侧直接移动到最左侧,而是必须经过中间.求当塔有N层的时候,打印最优移动过程和最优移动总步数. [解答] 上一篇用的是递归的方法解决这个问题,这里我们用栈来模拟汉诺塔的三个塔,也就是不用递归的方法 原理是这样的:修改后的汉诺塔问题不能让任何塔从左直接移动到右,也不能从右直接移动到左,而是要经过中间,也就是说,实际上能做的动作,只有四个:左->中,中->左,中->右,右->中 用栈

  • JAVA数据结构之汉诺塔代码实例

    本文实例为大家分享了JAVA数据结构之汉诺塔的具体代码,供大家参考,具体内容如下 package p02.动态链表; import p01.动态数组.Stack; public class LinkedStack<E> implements Stack<E> { private LinkedList<E> list; public LinkedStack(){ list=new LinkedList<>(); } @Override public void

  • Java 实现一个汉诺塔实战练习

    Java 实现一个汉诺塔实战练习

    汉诺塔简介: 我们想要实现的是 让 A柱上的盘子,移动到C柱上 1层汉诺塔 2层汉诺塔 3层汉诺塔详解图 第一步 第二步 第三步 第四步 第五步 第六步 第七步 经过上面的图解,相比大家一定在一定程度了解到汉诺塔的游戏规则,以及怎么去玩. 总之 最终C柱上第一个盘子,是最大,最顶的是最小的,而且在操作过程中,前几步就是为了让三个柱子中最大的盘子移动到C柱上, 然后不断,将它两个柱子中最大盘子往上累加,(盘子从大到小,从下往上摆放) 而且盘子一多,你就会发现过程中间,除了最大的盘子,其余的盘子都会

  • java递归实现汉诺塔步骤介绍

    java递归实现汉诺塔步骤介绍

    汉诺塔的规则是:一共三根柱子,一根柱子从上到下套着有小到大的若干个圆盘,要将所有圆盘按照这个排放顺序移动到第三根柱子上,并且每次只能移动一个圆盘. 可以将整个过程分为三个步骤来看: 第一步:将除最大圆盘外的n-1个圆盘移动辅助柱子上 第二步:将最大的圆盘移动到目标柱子 第三步:将n-1个圆盘从辅助柱子移动到目标柱子 其中第一步又可以拆成一模一样的三步,可以看成一个n-1层的塔要移动到目标柱子,只不过目标柱子换了一个: 第三步也可以拆分成一模一样的三步: 多拆几次就会发现规律:第一步和第三步无论如

  • Java SE求解汉诺塔问题的示例代码

    Java SE求解汉诺塔问题的示例代码

    目录 1.问题描述 2.画图分析 3.问题讲解 4.代码实现 1.问题描述 汉诺塔问题是一个经典的问题.汉诺塔(Hanoi Tower),又称河内塔,源于印度一个古老传说. 大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘. 大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上. 并且规定,任何时候,在小圆盘上都不能放大圆盘,且在三根柱子之间一次只能移动一个圆盘. 问应该如何操作? 2.画图分析 一个圆盘的情况:移动前 移动后 1个盘子:A直

  • C#解决汉诺塔问题DEMO

    C#解决汉诺塔问题DEMO

    汉诺塔问题是学习递归的入门问题,这里用C#简单实现了一个汉诺塔之间传递盘子的小程序 通过简单绘图实现盘子在几个塔之间的转换: namespace 汉诺塔 { //盘子类 class HanioItem { public int HanoiItemHeight { get; set; }//盘子的高度 public int HanoiItemWidth { get; set; }//盘子的宽度 public Point HanoiItemPoint { get; set; }//画盘子的起始点 }

  • java 实现汉诺塔详解及实现代码

    java 实现汉诺塔详解及实现代码 汉诺塔问题:有三根柱子A,B,C,其中A上面有n个圆盘,从上至下圆盘逐渐增大,每次只能移动一个圆盘,并且规定大的圆盘不能叠放在小的圆盘上面,现在想要把A上面的n个圆盘全部都移动到C上面,输出移动的总步数以及移动的过程 分析: //先求出移动的总步数 1,假设g(n)表示n个圆盘时的移动总的步数,当n=1时,g(1)=1; 2.现在可以把g(n)进行细分为三步: 1>先将n-1个圆盘从A通过C移动到B上面,相当于将n-1个圆盘从A移动到C,因此需要g(n-1)步

  • java 汉诺塔Hanoi递归、非递归(仿系统递归)和非递归规律 实现代码

    程序如下: 复制代码 代码如下: View Code  /*  * Hanoi塔游戏 问题描述:  * 汉诺塔:汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具.  * 大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照  * 大小顺序摞着64片黄金圆盘.大梵天命令婆罗门把圆盘从下面开始按大小  * 顺序重新摆放在另一根柱子上.并且规定,在小圆盘上不能放大圆盘,在  * 三根柱子之间一次只能移动一个圆盘.  *   * fuction:实现 hanoi塔  *       

随机推荐