C++实现AVL树的完整代码

AVL树的介绍

AVL树是一种自平衡的二叉搜索树，它通过单旋转（single rotate）和双旋转(double rotate)的方式实现了根节点的左子树与右子树的高度差不超过1,。这有效的降低了二叉搜索树的时间复杂度，为O（log n）。那么，下面小编将详细介绍C++实现AVL树的代码。最后一步提供可靠的代码实现

这里先粘贴代码
给大家的忠告，一定要及时去实现，不然之后再实现要花更多的时间

/*
 *平衡二叉树应该有些功能
 *插入 删除 查找
 *前序遍历 中序遍历 后序遍历 层次遍历
 *统计结点数目
 */
 //代码已经调好，写了很久才写出来

#ifndef _AVLTREE_
#define _AVLTREE_
#include<iostream>
#include<vector>
#include<queue>
#include<map>
using namespace std;
#define MAXFACTOR = 2;
template<class Key , class E>
class AVLNode
{
    private:
        Key key;
        E value;
        AVLNode<Key,E>* left;
        AVLNode<Key,E>* right;
        AVLNode<Key,E>* parent;
    public:
        AVLNode():left(nullptr),right(nullptr),parent(nullptr){}
        AVLNode(Key _key,E _value , AVLNode<Key,E>* _parent = nullptr,AVLNode<Key,E>*_left = nullptr, AVLNode<Key,E>*_right = nullptr):
                key(_key),value(_value),left(_left),right(_right),parent(_parent){}

        bool isLeaf(){return left==nullptr && right == nullptr ;}

        //元素设置
        Key getKey() const { return key;}
        void setKey(Key set) {key = set;}

        E getValue() const { return value;}
        void setValue(E set) {value = set;}

        AVLNode<Key,E>*  getLeft() { return left; }
        void setLeft (AVLNode< Key,E >* set){ left = set;}

        AVLNode<Key,E>*  getRight()  { return right;}
        void setRight (AVLNode<Key,E>* set) {right = set ;}

        AVLNode<Key,E>* getParent()  {return parent;}
        void setParent(AVLNode<Key,E>* set) { parent = set;}

};
template<class Key , class E>
class AVLTree
{
    private:
        AVLNode<Key,E>* root;
        void clear(AVLNode<Key,E>* &r)
        {
            if(r==nullptr)return;

            if(r->getLeft())clear(r->getLeft());
            if(r->getRight())clear(r->getRight);

            delete r;
        }

        void Init()
        {
            root = new AVLNode<Key,E>();
            root=nullptr;
        }
        void preOrder(AVLNode<Key,E>* r,void(*visit) (AVLNode<Key,E> * node))
        {
            if(r==nullptr)return;
            (*visit) (r);
            preOrder(r->getLeft() , visit);
            preOrder(r->getRight(), visit);
        }

        void inOrder(AVLNode<Key,E>* r , void(*visit)(AVLNode<Key,E>* node) )
        {
            if(r==nullptr)return;
            inOrder(r->getLeft() , visit);
            (*visit)(r);
            inOrder(r->getRight(),visit);
        }

        void postOrder(AVLNode<Key,E>*r , void (*visit) (AVLNode<Key,E>* node))
        {
            if(r==nullptr)return;
            postOrder(r->getLeft(),visit);
            postOrder(r->getRight(),visit);
            (*visit)(r);
        }

        void levelOrder(AVLNode<Key,E>*r , void (*visit) (AVLNode<Key,E>* node))
        {
            queue< AVLNode<Key,E>* > q;
            if(r==nullptr)return;
            q.push(r);
            while( ! q.empty() )
            {
                AVLNode<Key,E>* tmp = q.front();
                q.pop();
                (*visit)(tmp);
                if(tmp->getLeft() ) q.push(tmp->getLeft() );
                if(tmp->getRight()) q.push(tmp->getRight());

            }
        }

        AVLNode<Key,E>* find(AVLNode<Key,E>* r,Key k)
        {
            if(r==nullptr)return nullptr;
            if(k == r->getKey() ) return r;
            else if( k < r->getKey())
            {
                find(r->getLeft(),k);
            }
            else {
                find(r->getRight(),k);
            }
        }
        //Find the smallest element in the avl tree
        AVLNode<Key,E>* getMin(AVLNode<Key,E>* r)
        {
            if(r->getLeft() == nullptr) return r;
            else{
                getMin(r->getLeft());
            }
        }
        //Remove the smallest element
        AVLNode<Key,E>* deleteMin(AVLNode<Key,E>* rt)
        {
            if(rt->getLeft() == nullptr) return rt->getRight();
            else{
                rt->setLeft(deleteMin(rt->getLeft()));
                return rt;
            }
        }

        AVLNode<Key,E>* leftRotate(AVLNode<Key,E>* node)
        {
            if( node == nullptr) return nullptr;
            AVLNode<Key,E>* newHead = node->getRight();
            node->setRight( newHead -> getLeft() );
            newHead -> setLeft( node );
            return newHead;
        }
        AVLNode<Key,E>* rightRotate(AVLNode<Key,E>* node)
        {
            if(node == nullptr)return nullptr;
            AVLNode<Key,E>* newHead = node->getLeft();
            node->setLeft( newHead->getRight() );
            newHead ->setRight(node);
            return newHead;
        }

        int getHeight(AVLNode<Key,E>*node)
        {
            if(node == nullptr)return 0;
            if(node->isLeaf())return 1;
            else return ( getHeight( node->getLeft() ) > getHeight( node->getRight() ) ?
                        getHeight( node->getLeft() ) : getHeight( node->getRight() ) ) + 1;
        }

        int getBalanceFactor(AVLNode<Key,E>* node)
        {
            return getHeight(node->getLeft()) - getHeight(node->getRight() );
        }
        AVLNode<Key,E>* balance(AVLNode<Key,E>* node)
        {
            if(!node) return nullptr;
            else if ( getBalanceFactor( node ) == 2)
            {
                if(getBalanceFactor( node ->getLeft() ) == 1)
                {
                    node = rightRotate(node);
                }
                else
                {
                    node->setLeft(leftRotate( node->getLeft() ) );
                    node = rightRotate(node);
                }
            }
            else if(getBalanceFactor( node ) == -2)
            {
                if(getBalanceFactor( node->getRight()) == -1)
                {
                    node = leftRotate(node);
                }
                else
                {
                    node->setRight( rightRotate( node->getRight() ) );
                    node = leftRotate(node);
                }
            }
            return node;
        }

        AVLNode<Key,E>* insert( AVLNode<Key,E>* root ,const pair<Key,E>& it)
        {
            if(root == nullptr)
            {
                return new AVLNode<Key,E>(it.first , it.second,NULL,NULL,NULL);
            }
            else if (it.first < root->getKey() )
            {

                root ->setLeft( insert(root->getLeft() , it) ) ;
            }
            else{
                root ->setRight( insert(root->getRight() , it) );

            }
            root = balance(root);
            return root;
        }

        AVLNode<Key,E>* remove(AVLNode<Key,E>*  node , const Key k)
        {
            if(node == nullptr) return nullptr;
            if(node->getKey() > k)
            {
                node->setLeft( remove(node->getLeft() , k) );
                node = balance(node);
            }
            else if(node->getKey() < k)
            {
                node->setRight( remove(node->getRight(), k) );
                node = balance(node);
            }
            else if(node->getKey() == k)
            {
                if(! node->isLeaf() )
                {
                    AVLNode<Key,E>* tmp = getMin(node->getRight() );
                    node->setKey( tmp->getKey() );
                    node->setValue( tmp->getValue() );
                    node->setRight( deleteMin(node->getRight() ) );
                    delete tmp;
                }
                else {
                    AVLNode<Key,E>* tmp = node;
                    node = (node->getLeft() != nullptr) ? node->getLeft() : node->getRight() ;
                    delete tmp;
                }
            }
            return node;
        }

    public:
        ~AVLTree(){clear(root);}
        AVLTree(){/*Init();*/ root = nullptr; }
    //四种遍历方式
        void preOrder( void (*visit)(AVLNode<Key,E>* r))
        {
            preOrder(root,visit);
        }
        void inOrder(void (*visit)(AVLNode<Key,E>* r))
        {
            inOrder(root,visit);
        }
        void postOrder(void (*visit)(AVLNode<Key,E>* r))
        {
            postOrder(root,visit);
        }
        void levelOrder( void(*visit)(AVLNode<Key,E>*r) )
        {
            levelOrder(root,visit);
        }
         //插入
        void insert(const pair<Key,E> &it)
        {
            root = insert(root,it);
        }

        //删除
       void remove(const Key& k)
        {
            remove(root,k);
        }
        bool find(const Key&k)
        {
            return find(root,k);
        }   

};
#endif

//AVLtest.cpp
#include"NewAvl.h"
#include<iostream>
using namespace std;
template<typename Key,typename E>
void traverse(AVLNode<Key,E>* root)
{
    cout<<root->getKey()<<" "<<root->getValue()<<" ";
    cout<<endl;
}
int main()
{
    AVLTree<int,int>* tree = new AVLTree<int ,int>;
    for(int i = 0 ; i < 5 ; i ++)
    {
        tree->insert(make_pair(i,i));
    }
    tree->remove(1);
    cout<<"PreOrder: "<<endl;
    tree->preOrder(traverse);
    cout<<endl;
    cout<<"LevelOrder: "<<endl;
    tree->levelOrder(traverse);
    cout<<endl;
    cout<<"InOrder: "<<endl;
    tree->inOrder(traverse);
    cout<<endl;
    cout<<"PostOrder: "<<endl;
    tree->postOrder(traverse);
    cout<<endl;
    cout<<tree->find(2)<<endl;
    tree->insert(make_pair(9,9));
    tree->levelOrder(traverse);

}

运行结果

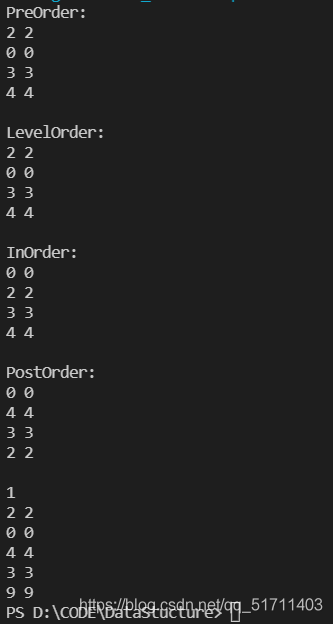
以上就是C++实现AVL树的完整代码的详细内容，更多关于C++ AVL树的资料请关注我们其它相关文章！