Python 阶乘详解

相信大家对阶乘都不陌生。不知道阶乘的可以看这里：

一个数的阶乘：

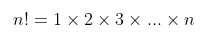
比如5的阶乘

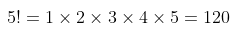
在python中大部分教程一般推荐用递归函数完成：

#!/usr/bin/python3
"""Python2，3都可以"""
def factorial(n):#主体函数
    if n == 1:
        return 1
    return n * factorial(n-1)
res = input("请输入n:")
print(factorial(res))

但是这样不仅阅读不方便，还有可能在n非常大时造成栈溢出的情况。

>>> factorial(1000)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "<stdin>", line 4, in factorial
  File "<stdin>", line 4, in factorial
  File "<stdin>", line 4, in factorial
  [Previous line repeated 995 more times]
  File "<stdin>", line 2, in factorial
RecursionError: maximum recursion depth exceeded in comparison

所以我更倾向于这个：

#!/usr/bin/python
li = []
def factorial(n):
    global li
    result = 1
    for i in range(n):
        li.append(i+1)
    for j in li:
        result = result * j
    return result
print(factorial(int(input("请输入n:"))))

通过单一列表存储，可以有效减少内存使用，并且这个调用只占用几个栈，不会造成溢出。

或者math模块中也有函数可以使用：

import math
a = input("N:")
fac = math.factorial(a)
print(fac)

要么就是非常简单的for:

#中文变量名是合法的!
#中文变量名是合法的!!
#中文变量名是合法的!!!
数 = input("数:")
a = 1
for i in range(1,数+1):
    a = a * i
print(a)

非常容易理解~

参考：https://docs.python.org/3

总结

本篇文章就到这里了，希望能够给你带来帮助，也希望您能够多多关注我们的更多内容！

赞 (0)

相关推荐

  • Python阶乘求和的代码详解

    Python阶乘求和的方法 题目描述: 获得用户输入的整数n,输出 1!+2!+-+n!的值. 如果输入数值为0.负数.非数字或非整数,输出提示信息:输入有误,请输入正整数. 方法一: #factTest1 def main(): a = input() sum = 0 if a.isdigit(): n = eval(a) if n > 0: fact = 1 for i in range(1, n+1): fact *= i sum += fact print(sum) else: prin

  • 详解用python计算阶乘的几种方法

    第一种:利用functools 工具处理 import functools result = (lambda k: functools.reduce(int.__mul__, range(1, k + 1), 1))(5) print(result) 第二种:普通的循环 x = 1 y = int(input("请输入要计算的数:")) for i in range(1, y + 1): x = x * i print(x) 第三种:利用递归的方式 def func(n): if n

  • python求前n个阶乘的和实例

    我就废话不多说了,还是直接看代码吧! i = int(input("input")) sum = 0 if i<1: exit() else: while i>0: b = 2 c = 1 while b<=i: c=b*c b=b+1 sum += c i = i-1 # print(c) print(sum) 补充知识:python 利用递归方法求解n的阶乘和 写程序算出n的阶乘的和 def fn(x): if x==1: return 1 def f(x): i

  • python递归函数求n的阶乘,优缺点及递归次数设置方式

    递归函数两大特点: 1.能够调用函数自身 2.至少有一个出口(结束函数自身调用) 函数实现: def calnum(num): if num != 1: # 递归调用自身函数 csum = num * calnum(num - 1) else: # 设置递归出口 csum = 1 return csum ret = calnum(5) print(ret) 递归函数的缺点: 占用资源多,一般不会优先选择. 一个程序中python默认只允许调用自身1024次,超过这个次数, python解释器会认

  • python计算n的阶乘的方法代码

    整数的阶乘(英语:factorial)是所有小于及等于该数的正整数的积,0的阶乘为1.即:n!=1×2×3×...×n. 首先导入math模块,然后调用factorial()函数来计算阶乘. 1 math.factorial(x) import math value = math.factorial(x) 2. reduce函数 def factorial(n): return reduce(lambda x,y:x*y,[1]+range(1,n+1)) 3. 递归实现 def factori

  • Python 阶乘详解

    Python 阶乘详解

    相信大家对阶乘都不陌生.不知道阶乘的可以看这里: 一个数的阶乘: 比如5的阶乘 在python中大部分教程一般推荐用递归函数完成: #!/usr/bin/python3 """Python2,3都可以""" def factorial(n):#主体函数 if n == 1: return 1 return n * factorial(n-1) res = input("请输入n:") print(factorial(res))

  • Python实例详解递归算法

    Python实例详解递归算法

    递归是一种较为抽象的数学逻辑,可以简单的理解为「程序调用自身的算法」. 维基百科对递归的解释是: 递归(英语:Recursion),又译为递回,在数学与计算机科学中,是指在函数的定义中使用函数自身的方法.递归一词还较常用于描述以自相似方法重复事物的过程. 例如,当两面镜子相互之间近似平行时,镜中嵌套的图像是以无限递归的形式出现的.也可以理解为自我复制的过程. "递"是传递的意思,"归"是归还的意思,先把一个方法一层层传递下去,然后传递到最后一层再把结果归还回来. 比

  • Golang与python线程详解及简单实例

    Golang与python线程详解及简单实例 在GO中,开启15个线程,每个线程把全局变量遍历增加100000次,因此预测结果是 15*100000=1500000. var sum int var cccc int var m *sync.Mutex func Count1(i int, ch chan int) { for j := 0; j < 100000; j++ { cccc = cccc + 1 } ch <- cccc } func main() { m = new(sync.

  • python getopt详解及简单实例

     python getopt详解 函数原型: getopt.getopt(args, shortopts, longopts=[]) 参数解释: args:args为需要解析的参数列表.一般使用sys.argv[1:],这样可以过滤掉第一个参数(ps:第一个参数是脚本的名称,它不应该作为参数进行解析) shortopts:简写参数列表 longopts:长参数列表 返回值: opts:分析出的(option, value)列表对. args:不属于格式信息的剩余命令行参数列表. 源码分析 在An

  • Python注释详解

    注释用于说明代码实现的功能.采用的算法.代码的编写者以及创建和修改的时间等信息. 注释是代码的一部分,注释起到了对代码补充说明的作用. Python注释 Python单行注释以#开头,单行注释可以作为单独的一行放在被注释的代码行之上,也可以放在语句或者表达式之后. #Give you a chance to let you know me print("Give you a chance to let you know me") say_what = "this is a d

  • python 类详解及简单实例

    python 类详解 类 1.类是一种数据结构,可用于创建实例.(一般情况下,类封装了数据和可用于该数据的方法) 2.Python类是可调用的对象,即类对象 3.类通常在模块的顶层进行定义,以便类实例能够在类所定义的源代码文件中的任何地方被创建. 4.实例初始化 instance = ClassName(args....) 类在实例化时可以使用__init__和__del__两个特殊的方法. class ClassName(base): 'class documentation string'

  • 神经网络理论基础及Python实现详解

    神经网络理论基础及Python实现详解

    一.多层前向神经网络 多层前向神经网络由三部分组成:输出层.隐藏层.输出层,每层由单元组成: 输入层由训练集的实例特征向量传入,经过连接结点的权重传入下一层,前一层的输出是下一层的输入:隐藏层的个数是任意的,输入层只有一层,输出层也只有一层: 除去输入层之外,隐藏层和输出层的层数和为n,则该神经网络称为n层神经网络,如下图为2层的神经网络: 一层中加权求和,根据非线性方程进行转化输出:理论上,如果有足够多的隐藏层和足够大的训练集,可以模拟出任何方程: 二.设计神经网络结构 使用神经网络之前,必须

  • 对YOLOv3模型调用时候的python接口详解

    需要注意的是:更改完源程序.c文件,需要对整个项目重新编译.make install,对已经生成的文件进行更新,类似于之前VS中在一个类中增加新函数重新编译封装dll,而python接口的调用主要使用的是libdarknet.so文件,其余在配置文件中的修改不必重新进行编译安装. 之前训练好的模型,在模型调用的时候,总是在 lib = CDLL("/home/*****/*******/darknet/libdarknet.so", RTLD_GLOBAL)这里读不到darknet编译

  • .dcm格式文件软件读取及python处理详解

    要处理一些.DCM格式的焊接缺陷图像,需要读取和显示.dcm格式的图像.通过搜集资料收集到一些医学影像,并通过pydicom模块查看.dcm格式文件. 若要查看dcm格式文件,可下Echo viewer 进行查看. 若用过pycharm进行处理,可选用如下的代码: # -*-coding:utf-8-*- import cv2 import numpy import dicom from matplotlib import pyplot as plt dcm = dicom.read_file(

  • 最小二乘法及其python实现详解

    最小二乘法Least Square Method,做为分类回归算法的基础,有着悠久的历史(由马里·勒让德于1806年提出).它通过最小化误差的平方和寻找数据的最佳函数匹配.利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小.最小二乘法还可用于曲线拟合.其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达. 那什么是最小二乘法呢?别着急,我们先从几个简单的概念说起. 假设我们现在有一系列的数据点 ,那么由我们给出的拟合函数h(x)得到的估计量就是

随机推荐