Java 由浅入深带你掌握图的遍历

目录

• 1.图的遍历
• 2.深度优先遍历
• 3.利用DFS判断有向图是否存在环
• 4.广度优先遍历

1.图的遍历

从图中某一顶点出发访问图中其余顶点，且每个顶点仅被访问一次

图的遍历有两种深度优先遍历DFS、广度优先遍历BFS

2.深度优先遍历

深度优先遍历以深度为优先进行遍历，简单来说就是每次走到底。类似于二叉树的前序遍历

思路：

1.以某一个顶点为起点进行深度优先遍历，并标记该顶点已访问

2.以该顶点为起点选取任意一条路径一直遍历到底，并标记访问过的顶点

3.第2步遍历到底后回退到上一个顶点，重复第2步

4.遍历所有顶点结束

根据遍历思路可知，这是一个递归的过程，其实DFS与回溯基本相同。

遍历：

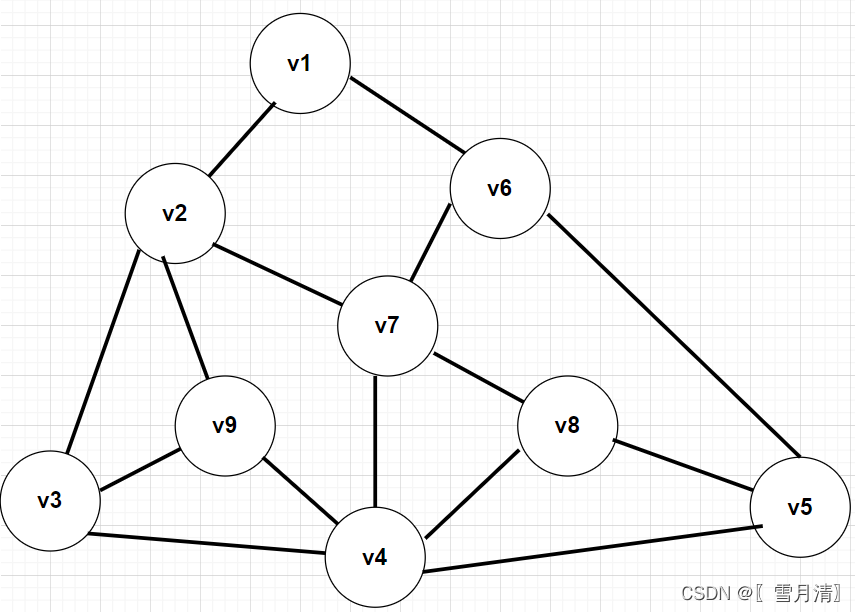
以此图为例进行深度优先遍历

	static void dfs(int[][] graph,int idx,boolean[]visit) {
		int len = graph.length;
		//访问过
	 if(visit[idx]) return;
	 //访问该顶点
	 System.out.println("V"+idx);
	 //标志顶点
	 visit[idx] = true;
	 for(int i = 1;i < len;i++) {
	 //访问该顶点相连的所有边
		 if(graph[idx][i] == 1) {
	 //递归进行dfs遍历
		 dfs(graph, i, visit);
		 }
	 }

	}

遍历结果：

V1

V2

V3

V4

V5

V6

V7

V8

V9

创建图的代码：

public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		//顶点数 以1开始
		int n = scanner.nextInt();
		int[][] graph = new int[n+1][n+1];
		//边数
		int m = scanner.nextInt();

		for(int i = 1;i <= m;i++) {
			int v1 = scanner.nextInt();
			int v2 = scanner.nextInt();
			graph[v1][v2] = 1;
			graph[v2][v1] = 1;
		}

		//标记数组 false表示未访问过
		boolean[] visit = new boolean[n+1];
		dfs(graph, 1, visit);

	}

3.利用DFS判断有向图是否存在环

思路：遍历某一个顶点时，如果除了上一个顶点之外，还存在其他相连顶点被访问过，则必然存在环

	//默认无环
   static boolean flag = false;
	public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		//顶点数 以1开始
		int n = scanner.nextInt();
		int[][] graph = new int[n+1][n+1];
		//边数
		int m = scanner.nextInt();

		for(int i = 1;i <= m;i++) {
			int v1 = scanner.nextInt();
			int v2 = scanner.nextInt();
			graph[v1][v2] = 1;

		}
	 //标记数组 true为访问过
		boolean[] visit = new boolean[n+1];
		dfs(graph, 1, visit,1);
		if(flag)
			System.out.println("有环");

	}

	static void dfs(int[][] graph,int idx,boolean[]visit,int parent) {
		int len = graph.length;

	 System.out.println("V"+idx);
	 //标记顶点
	 visit[idx] = true;
	 for(int i = 1;i < len;i++) {
		 //访问该顶点相连的所有边
		 if(graph[idx][i] == 1) {
		 if( !visit[i] ) {
		 dfs(graph, i, visit,idx);
		 }
		 else if(idx != i) {
			 flag = true;
		 }
		 }
	 }

	}

注意：是有向图判断是否存在环，无向图判断是否存在环无意义，因为任意两个存在路径的顶点都可以是环

4.广度优先遍历

广度优先遍历是以广度（宽度）为优先进行遍历。类似于二叉树的层序遍历

思路：

1.以某一个顶点为起点进行广度优先遍历，并标记该顶点已访问

2.访问所有与该顶点相连且未被访问过的顶点，并标记访问过的顶点

3.以第2步访问所得顶点为起点重复1、2步骤

4.遍历所有顶点结束

通过队列来辅助遍历，队列出队顺序即是广度优先遍历结果

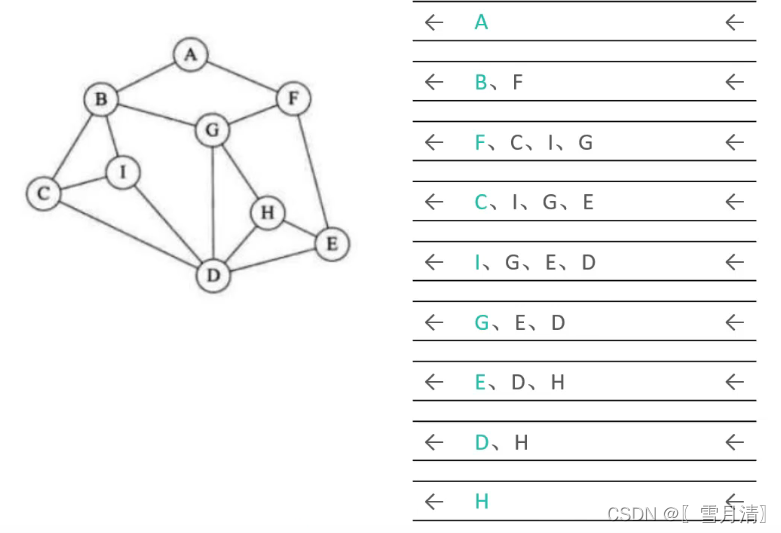
遍历

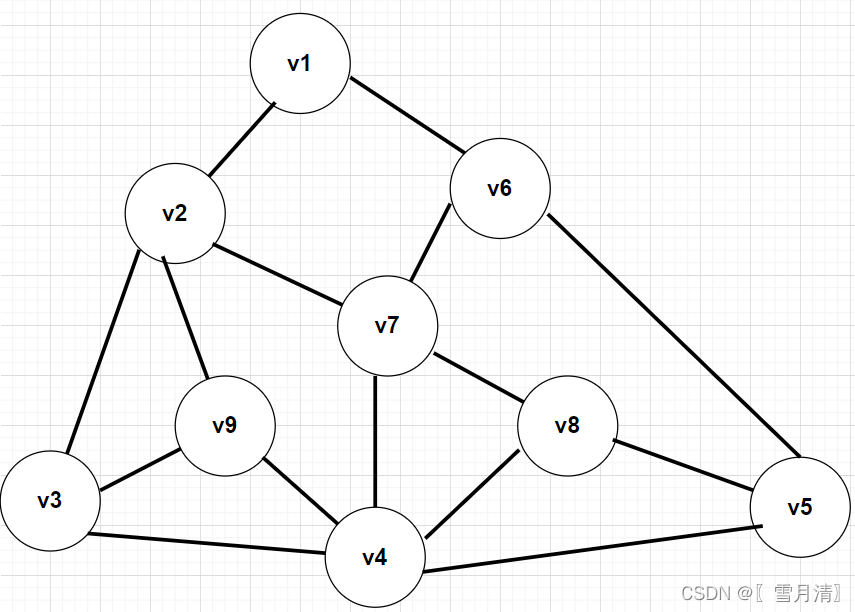
以此图为例，采用邻接矩阵的方式创建图，进行BFS遍历

	static void bfs(int[][] graph) {
		int len = graph.length;
		//标记数组 false表示未访问过
		boolean[] visit = new boolean[len];
		//辅助队列
		Queue<Integer> queue = new LinkedList<>();

		queue.offer(1);
		visit[1] = true;

		while(!queue.isEmpty()) {
			int num = queue.poll();
			System.out.println("V"+num);

			//遍历该顶点所有相连顶点
			for(int i = 1;i < len;i++) {
				//相连并且没有被访问过
				if(graph[num][i] == 1 && !visit[i]) {
					queue.offer(i);
					visit[i] = true;
				}
			}
		}
	}

遍历结果：

V1

V2

V6

V3

V7

V9

V5

V4

V8

创建图的代码

public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		//顶点数 以1开始
		int n = scanner.nextInt();
		int[][] graph = new int[n+1][n+1];
		//边数
		int m = scanner.nextInt();

		for(int i = 1;i <= m;i++) {
			int v1 = scanner.nextInt();
			int v2 = scanner.nextInt();
			graph[v1][v2] = 1;
			graph[v2][v1] = 1;
		}
		bfs(graph);
	}

到此这篇关于Java 由浅入深带你掌握图的遍历的文章就介绍到这了,更多相关Java 图的遍历内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！