C++ 二叉树的实现超详细解析

目录
  • 1、树的概念及结构(了解)
    • 1.1树的概念：
    • 1.2树的表示法：
  • 2、二叉树的概念及结构
    • 2.1二叉树的概念：
    • 2.2特殊的二叉树：
    • 2.3二叉树的性质：
    • 2.4二叉树的顺序存储：
    • 2.5二叉树的链式存储：
  • 3、二叉树链式结构的实现
    • 3.1二叉树的前中后序遍历：
    • 3.2求二叉树的节点个数：
    • 3.3求二叉树的叶子节点个数：
    • 3.4销毁二叉树：

1、树的概念及结构(了解)

1.1树的概念：

树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

  • 有一个特殊的结点，称为根结点，根节点没有前驱结点。
  • 除根节点外，其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm，其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有0个或多个后继。
  • 树是递归定义的。

子树是不相交的；除了根节点之外，每个节点有且仅有一个父节点；一棵N个节点的树有N-1条边。

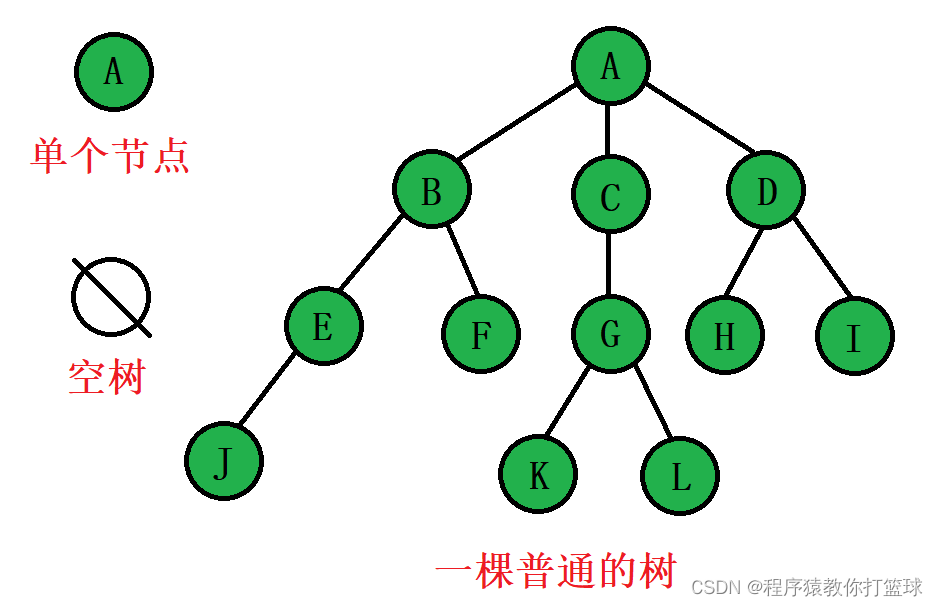
节点的度：一个节点含有的子树的个数称为该节点的度； 如上图：A的为3

叶节点或终端节点：度为0的节点称为叶节点； 如上图：J、F、K、L、H、I节点为叶节点

非终端节点或分支节点：度不为0的节点； 如上图：B、C、D、E..等节点为分支节点

双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点； 如上图：A是B的父节点

孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点； 如上图：B是A的孩子节点

兄弟节点：具有相同父节点的节点互称为兄弟节点； 如上图：B、C是兄弟节点

树的度：一棵树中，最大的节点的度称为树的度； 如上图：树的度为3

节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；

树的高度或深度：树中节点的最大层次； 如上图：树的高度为4

节点的祖先：从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先

子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙

森林：由m（m>0）棵互不相交的多颗树的集合称为森林；（数据结构中的学习并查集本质就是 一个森林）

1.2树的表示法：

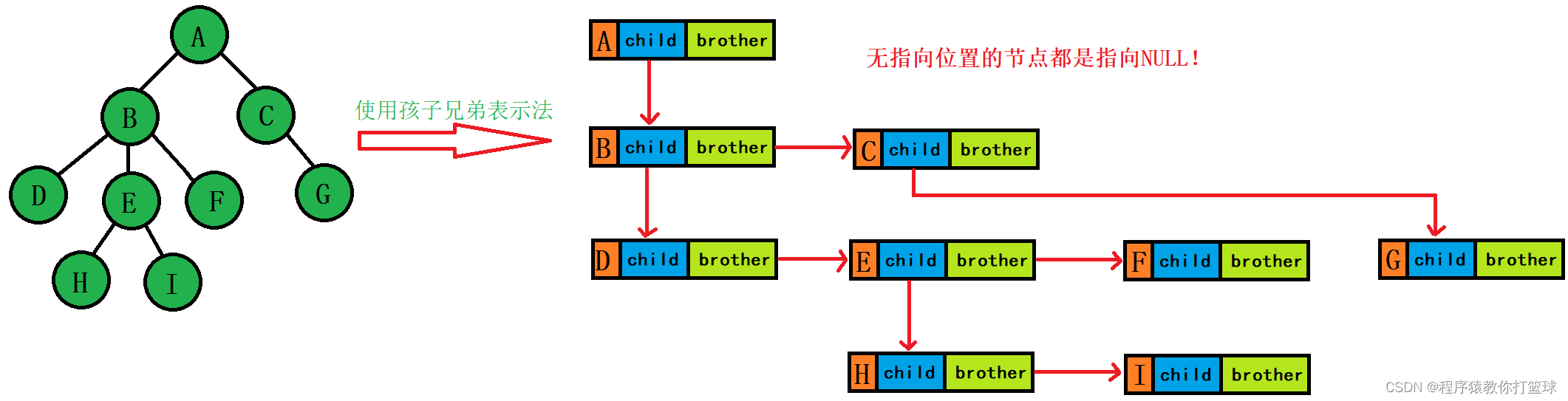
树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，实际中树有很多种表示方式， 如：双亲表示法，孩子表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子 兄弟表示法。(我们本期主要讲解二叉树)

typedef int DataType;
struct Node
{
    struct Node* _firstChild1;    // 第一个孩子结点
    struct Node* _pNextBrother;   // 指向其下一个兄弟结点
    DataType _data;               // 结点中的数据域
};

2、二叉树的概念及结构

2.1二叉树的概念：

一棵二叉树是结点的一个有限集合，该集合或者为空，或者是由一个根节点加上两棵别称为左子 树和右子树的二叉树组成。

二叉树的特点：

1. 每个结点最多有两棵子树，即二叉树不存在度大于2的结点。

2. 二叉树的子树有左右之分，其子树的次序不能颠倒。

2.2特殊的二叉树：

赞 (0)

相关推荐

  • C++实现LeetCode(199.二叉树的右侧视图)

    [LeetCode] 199.Binary Tree Right Side View 二叉树的右侧视图 Given a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom. For example: Given the following binary tree,    1     

  • C++ 非递归实现二叉树的前中后序遍历

    C++ 非递归实现二叉树的前中后序遍历

    目录 二叉树的前序遍历 二叉树的中序遍历 二叉树的后序遍历 二叉树的前序遍历 在不使用递归的方式遍历二叉树时,我们可以使用一个栈模拟递归的机制.二叉树的前序遍历顺序是:根 → 左子树 → 右子树,我们可以先将二叉树的左路结点入栈,在入栈的同时便对其进行访问,此时就相当于完成了根和左子树的访问,当左路结点入栈完毕后再从栈顶依次取出结点,并用同样的方式访问其右子树即可. 具体步骤如下: 将左路结点入栈,入栈的同时访问左路结点. 取出栈顶结点top. 准备访问top结点的右子树. struct Tre

  • C++二叉树的直径与合并详解

    C++二叉树的直径与合并详解

    目录 二叉树的直径 给定一棵二叉树,你需要计算它的直径长度.一棵二叉树的直径长度是任意两个结点路径长度中的最大值.这条路径可能穿过也可能不穿过根结点. 思路 合并二叉树 给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠.你需要将他们合并为一个新的二叉树.合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点. 思路 1.确定递归函数的参数和返回值: 2.确定终止条件: 3.确定单层递归的逻辑:

  • C++合并二叉树的思路与示例代码

    C++合并二叉树的思路与示例代码

    前言 给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠.你需要将他们合并为一个新的二叉树.合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点. 示例 1: 思路 1.确定递归函数的参数和返回值: 首先那么要合入两个二叉树,那么参数至少是要传入两个二叉树的根节点,返回值就是合并之后二叉树的根节点. 代码如下: TreeNode* mergeTrees(TreeNode* t1, TreeNod

  • C++实现LeetCode(156.二叉树的上下颠倒)

    [LeetCode] 156. Binary Tree Upside Down 二叉树的上下颠倒 Given a binary tree where all the right nodes are either leaf nodes with a sibling (a left node that shares the same parent node) or empty, flip it upside down and turn it into a tree where the origina

  • C++实现LeetCode(124.求二叉树的最大路径和)

    [LeetCode] 124. Binary Tree Maximum Path Sum 求二叉树的最大路径和 Given a non-empty binary tree, find the maximum path sum. For this problem, a path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child conn

  • C++ 二叉树的实现超详细解析

    C++ 二叉树的实现超详细解析

    目录 1.树的概念及结构(了解) 1.1树的概念: 1.2树的表示法: 2.二叉树的概念及结构 2.1二叉树的概念: 2.2特殊的二叉树: 2.3二叉树的性质: 2.4二叉树的顺序存储: 2.5二叉树的链式存储: 3.二叉树链式结构的实现 3.1二叉树的前中后序遍历: 3.2求二叉树的节点个数: 3.3求二叉树的叶子节点个数: 3.4销毁二叉树: 1.树的概念及结构(了解) 1.1树的概念: 树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合.把它叫做树是因为它看

  • Go语言单元测试超详细解析

    目录 一.单元测试分类及其概念 1.基本分类 2.细说单元测试分类 二.结合代码细说每一种测试 1.基准测试 2.组测试与子测试 三.pprof调试工具 1.对主函数进行传参 2.pprof性能调优 前言: 平时根据需求写代码.人工进行测试往往不会面面俱到,还会因为需求的改变繁琐的进行测试通过完成一个测试函数,可以大大简化测试的步骤,并且在需求该变的时候只需要改变一下测试的输入与期望 一.单元测试分类及其概念 1.基本分类 测试函数 函数前缀为Test 主要用于测试程序的一些逻辑行为是否正确 基

  • 超详细解析C++实现快速排序算法的方法

    目录 一.前言 1.分治算法 2.分治算法解题方法 二.快速排序 1.问题分析 2.算法设计 3.算法分析 三.AC代码 一.前言 1.分治算法 快速排序,其实是一种分治算法,那么在了解快速排序之前,我们先来看看什么是分治算法.在算法设计中,我们引入分而治之的策略,称为分治算法,其本质就是将一个大规模的问题分解为若干个规模较小的相同子问题,分而治之. 2.分治算法解题方法 1.分解: 将要解决的问题分解为若干个规模较小.相互独立.与原问题形式相同的子问题. 2.治理: 求解各个子问题.由于各个子

  • 超详细解析C++实现归并排序算法

    目录 一.前言 分治算法 分治算法解题方法 二.归并排序 1.问题分析 2.算法设计 3.算法分析 三.AC代码 一.前言 分治算法 归并排序,其实就是一种分治算法 ,那么在了解归并排序之前,我们先来看看什么是分治算法.在算法设计中,我们引入分而治之的策略,称为分治算法,其本质就是将一个大规模的问题分解为若干个规模较小的相同子问题,分而治之. 分治算法解题方法 1.分解: 将要解决的问题分解为若干个规模较小.相互独立.与原问题形式相同的子问题. 2.治理: 求解各个子问题.由于各个子问题与原问题

  • C++带头双向循环链表超详细解析

    C++带头双向循环链表超详细解析

    目录 什么是带头双向循环链表 带头双向循环链表常用接口实现 上期我们讲完了无头单向非循环链表,这期我们接着来讲链表中结构最复杂的带头双向循环链表! 本期主要内容: 什么是带头双向循环链表? 带头双向循环链表常用接口实现! 顺序表和链表的区别和联系! 什么是带头双向循环链表 什么是带头?双向?循环?(带头双向循环链表) 带头:代表链表存在一个哨兵位节点,也就是头节点,这个节点不存放任何的有效数据! 双向:每个节点都有两个指针,分别指向它的前一个节点和后一个节点! 循环:最后一个节点next不再指向

  • C++ 栈和队列的实现超详细解析

    C++ 栈和队列的实现超详细解析

    目录 1.栈的介绍: 2.栈的常用接口实现 3.队列的介绍 4.队列的常用接口实现 可算是把链表给结束了,很多小伙伴已经迫不及待想看到栈和队列了,那么它来了!相信有了顺序表和链表的基础,栈和队列对于你们来讲也是轻轻松松,那我就废话不多说,直接进入今天的重点: 1.栈的介绍: 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作.进行数据插入和删除操作的一端称为栈顶,另一端称为栈底.栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则. 压栈:栈的插入操作叫做

  • Python超详细分步解析随机漫步

    Python超详细分步解析随机漫步

    创建RandomWalk类 为模拟随机漫步,我们将创建一个RandomWalk类,随机选择前进方向,这个类有三个属性,一个存储随机漫步的次数,另外两个存储随机漫步的每个点的x,y坐标,每次漫步都从点(0,0)出发 from random import choice class RandomWalk(): '''一个生成随机漫步数据的类''' def __init__(self,num_points=5000): '''初始化随机漫步的属性''' self.num_points = num_poi

  • C语言 超详细总结讲解二叉树的概念与使用

    C语言 超详细总结讲解二叉树的概念与使用

    目录 1.二叉树的概念及结构 2.二叉树链式结构的实现 1.二叉树的概念及结构 ①概念:一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成. ②二叉树的特点: 每个结点最多有两棵子树,即二叉树不存在度大于2的结点.(度最多为2) 二叉树的子树有左右之分,其子树的次序不能颠倒. ③现实中的二叉树: 当一名普通的人看到这样一颗树,可能会想:好标准的一棵树 当一个程序猿看到这样一棵树,可能会想:好像数据结构中的二叉树,并且还是颗满二叉树 ④数据结

  • C语言数据结构详细解析二叉树的操作

    C语言数据结构详细解析二叉树的操作

    目录 二叉树分类 二叉树性质 性质的使用 二叉树的遍历 前序遍历 中序遍历 后序遍历 层序遍历 求二叉树的节点数 求二叉树叶子结点个数 求二叉树的最大深度 二叉树的销毁 二叉树分类 满二叉树 除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树.也可以理解为每一层的结点数都达到最大值的二叉树. 完全二叉树 一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下.从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为

  • C++超详细讲解树与二叉树

    C++超详细讲解树与二叉树

    目录 树 树的定义 树的名词解释 树的表示 树的存储结构 二叉树的概念及结构 二叉树的概念 二叉树的性质 二叉树的存储结构 顺序存储结构 链式存储结构 树 树的定义 Q:什么是树 A:树是一种 非线性 的数据结构,它是由 n ( n>=0 )个有限结点组成一个具有层次关系的集合.把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的. Q:树有什么特点 有一个特殊的结点,称为根结点,根节点没有前驱结点. 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1.T2.…….T

随机推荐