Python实现二叉搜索树

二叉搜索树

我们已经知道了在一个集合中获取键值对的两种不同的方法。回忆一下这些集合是如何实现ADT（抽象数据类型）MAP的。我们讨论两种ADT MAP的实现方式，基于列表的二分查找和哈希表。在这一节中，我们将要学习二叉搜索树，这是另一种键指向值的Map集合，在这种情况下我们不用考虑元素在树中的实际位置，但要知道使用二叉树来搜索更有效率。

搜索树操作

在我们研究这种实现方式之前，让我们回顾一下ADT MAP提供的接口。我们会注意到，这种接口和Python的字典非常相似。

1. Map() 创建了一个新的空Map集合。
2. put(key,val) 在Map中增加了一个新的键值对。如果这个键已经在这个Map中了，那么就用新的值来代替旧的值。
3. get(key) 提供一个键，返回Map中保存的数据，或者返回None。
4. del 使用del map[key]这条语句从Map中删除键值对。
5. len() 返回Map中保存的键值对的数目
6. in 如果所给的键在Map中，使用key in map这条语句返回True。

搜索树实现

一个二叉搜索树，如果具有左子树中的键值都小于父节点，而右子树中的键值都大于父节点的属性，我们将这种树称为BST搜索树。如之前所述的，当我们实现Map时，BST方法将引导我们实现这一点。图 1 展示了二叉搜索树的这一特性，显示的键没有关联任何的值。注意这种属性适用于每个父节点和子节点。所有在左子树的键值都小于根节点的键值，所有右子树的键值都大于根节点的键值。

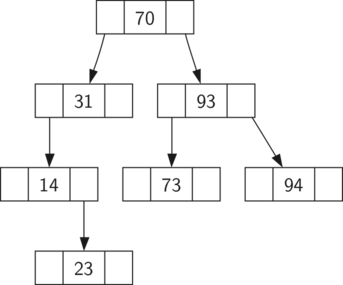
图 1：一个简单的二叉搜索树

现在你知道什么是二叉搜索树了，我们再来看如何构造一个二叉搜索树，我们在搜索树中按图 1 显示的节点顺序插入这些键值，图 1 搜索树存在的节点：70,31,93,94,14,23,73。因为 70 是第一个被插入到树的值，它是根节点。接下来，31 小于 70，因此是 70 的左子树。接下来，93 大于 70，因此是 70 的右子树。我们现在填充了该树的两层，所以下一个键值，将会是 31 或者 93 的左子树或右子树。由于 94 大于 70 和 93，就变成了 93 的右子树。同样，14 小于 70 和 31，因此成为了 31 的左子树。23 也小于 31，因此必须是 31 的左子树。然而，它大于 14，所以是 14 的右子树。

为了实现二叉搜索树，我们将使用节点和引用的方法，这类似于我们实现链表和表达式树的过程。因为我们必须能够创建和使用一个空的二叉搜索树，所以我们将使用两个类来实现，第一个类我们称之为 BinarySearchTree，第二个类我们称之为TreeNode。BinarySearchTree类有一个TreeNode类的引用作为二叉搜索树的根，在大多数情况下，外部类定义的外部方法只需检查树是否为空，如果在树上有节点，要求BinarySearchTree类中含有私有方法把根定义为参数。在这种情况下，如果树是空的或者我们想删除树的根，我们就必须采用特殊操作。BinarySearchTree类的构造函数以及一些其他函数的代码如Listing 1 所示。

Listing 1

class BinarySearchTree:

  def __init__(self):
    self.root = None
    self.size = 0

  def length(self):
    return self.size

  def __len__(self):
    return self.size

  def __iter__(self):
    return self.root.__iter__()

TreeNode类提供了许多辅助函数，使得BinarySearchTree类的方法更容易实现过程。如Listing 2 所示，一个树节点的结构，是由这些辅助函数实现的。正如你看到的那样，这些辅助函数可以根据自己的位置来划分一个节点作为左或右孩子和该子节点的类型。TreeNode类非常清楚地跟踪了每个父节点的属性。当我们讨论删除操作的实现时，你将明白为什么这很重要。

对于Listing 2 中的TreeNode实现，另一个有趣的地方是，我们使用Python的可选参数。可选的参数很容易让我们在几种不同的情况下创建一个树节点，有时我们想创建一个新的树节点，即使我们已经有了父节点和子节点。与现有的父节点和子节点一样，我们可以通过父节点和子节点作为参数。有时我们也会创建一个包含键值对的树，我们不会传递父节点或子节点的任何参数。在这种情况下，我们将使用可选参数的默认值。

Listing 2

class TreeNode:
  def __init__(self,key,val,left=None,right=None,
                    parent=None):
    self.key = key
    self.payload = val
    self.leftChild = left
    self.rightChild = right
    self.parent = parent

  def hasLeftChild(self):
    return self.leftChild

  def hasRightChild(self):
    return self.rightChild

  def isLeftChild(self):
    return self.parent and self.parent.leftChild == self

  def isRightChild(self):
    return self.parent and self.parent.rightChild == self

  def isRoot(self):
    return not self.parent

  def isLeaf(self):
    return not (self.rightChild or self.leftChild)

  def hasAnyChildren(self):
    return self.rightChild or self.leftChild

  def hasBothChildren(self):
    return self.rightChild and self.leftChild

  def replaceNodeData(self,key,value,lc,rc):
    self.key = key
    self.payload = value
    self.leftChild = lc
    self.rightChild = rc
    if self.hasLeftChild():
      self.leftChild.parent = self
    if self.hasRightChild():
      self.rightChild.parent = self

现在，我们拥有了BinarySearchTree和TreeNode类，是时候写一个put方法使我们能够建立二叉搜索树。put方法是BinarySearchTree类的一个方法。这个方法将检查这棵树是否已经有根。如果没有，我们将创建一个新的树节点并把它设置为树的根。如果已经有一个根节点，我们就调用它自己，进行递归，用辅助函数_put按下列算法来搜索树：

从树的根节点开始，通过搜索二叉树来比较新的键值和当前节点的键值，如果新的键值小于当前节点，则搜索左子树。如果新的关键大于当前节点，则搜索右子树。

当搜索不到左（或右）子树，我们在树中所处的位置就是设置新节点的位置。
向树中添加一个节点，创建一个新的TreeNode对象并在这个点的上一个节点中插入这个对象。

Listing 3 显示了在树中插入新节点的Python代码。_put函数要按照上述的步骤编写递归算法。注意，当一个新的子树插入时，当前节点（CurrentNode）作为父节点传递给新的树。

我们执行插入的一个重要问题是重复的键值不能被正确的处理，我们的树实现了键值的复制，它将在右子树创建一个与原来节点键值相同的新节点。这样做的后果是，新的节点将不会在搜索过程中被发现。我们用一个更好的方式来处理插入重复的键值，旧的值被新键关联的值替换。我们把这个错误的修复，作为练习留给你。

Listing 3

def put(self,key,val):
  if self.root:
    self._put(key,val,self.root)
  else:
    self.root = TreeNode(key,val)
  self.size = self.size + 1

def _put(self,key,val,currentNode):
  if key < currentNode.key:
    if currentNode.hasLeftChild():
        self._put(key,val,currentNode.leftChild)
    else:
        currentNode.leftChild = TreeNode(key,val,parent=currentNode)
  else:
    if currentNode.hasRightChild():
        self._put(key,val,currentNode.rightChild)
    else:
        currentNode.rightChild = TreeNode(key,val,parent=currentNode)

随着put方法的实现，我们可以很容易地通过__setitem__方法重载[]作为操作符来调用put方法（参见Listing 4）。这使我们能够编写像myZipTree['Plymouth'] = 55446一样的python语句，这看上去就像Python的字典。

Listing 4

def __setitem__(self,k,v):
  self.put(k,v)

图 2 说明了将新节点插入到一个二叉搜索树的过程。灰色节点显示了插入过程中遍历树节点顺序。

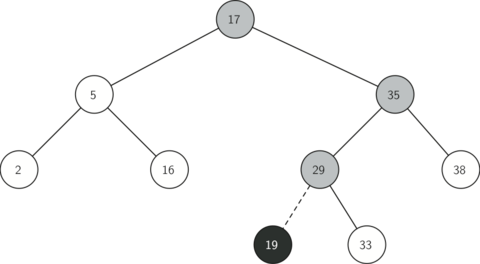
图 2: 插入一个键值 = 19 的节点

一旦树被构造，接下来的任务就是为一个给定的键值实现检索。get方法比put方法更容易因为它只需递归搜索树，直到发现不匹配的叶节点或找到一个匹配的键值。当找到一个匹配的键值后，就会返回节点中的值。

Listing 5 显示了get，_get和__getitem__的代码。用_get方法搜索的代码与put方法具有相同的选择左或右子树的逻辑。请注意，_get方法返回TreeNode中get的值，_get就可以作为一个灵活有效的方式，为BinarySearchTree的其他可能需要使用TreeNode里的数据的方法提供参数。

通过实现__getitem__方法，我们可以写一个看起来就像我们访问字典一样的Python语句，而事实上我们只是操作二叉搜索树，例如Z = myziptree ['fargo']。正如你所看到的，__getitem__方法都是在调用get。

Listing 5

def get(self,key):
  if self.root:
    res = self._get(key,self.root)
    if res:
        return res.payload
    else:
        return None
  else:
    return None

def _get(self,key,currentNode):
  if not currentNode:
    return None
  elif currentNode.key == key:
    return currentNode
  elif key < currentNode.key:
    return self._get(key,currentNode.leftChild)
  else:
    return self._get(key,currentNode.rightChild)

def __getitem__(self,key):
  return self.get(key)

使用get，我们可以通过写一个BinarySearchTree的__contains__方法来实现操作，__contains__方法简单地调用了get方法，如果它有返回值就返回True，如果它是None就返回False。如Listing 6 所示。

Listing 6

def __contains__(self,key):
  if self._get(key,self.root):
    return True
  else:
    return False

回顾一下__contains__重载的操作符，这允许我们写这样的语句：

if 'Northfield' in myZipTree:
  print("oom ya ya")