java实现二叉树遍历的三种方式

本文实例为大家分享了java实现二叉树遍历的具体代码，供大家参考，具体内容如下

二叉树如下：

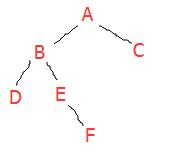
遍历结果如下：

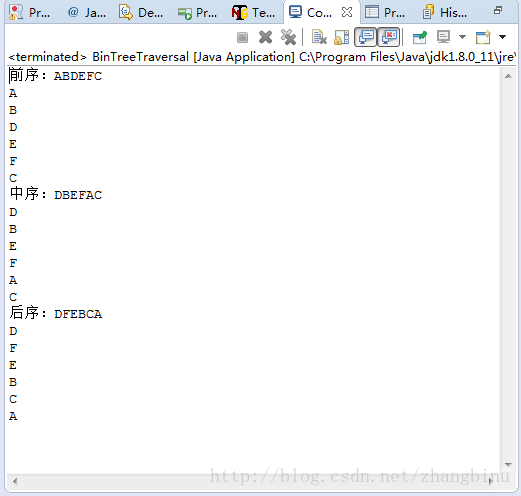
以下是实现代码：

package binTree;

import java.util.Stack;

/**
 * @author bin.zhang
 * @version 2017年8月29日 上午10:22:01
 */
public class BinTreeTraversal {
 public static void main(String[] args) {
  System.out.print("前序：");
  Traversal.preOrder();
  Traversal.preOrderRecursion(Traversal.createBinTree());
  System.out.print("中序：");
  Traversal.inOrder();
  Traversal.inOrderRecursion(Traversal.createBinTree());
  System.out.print("后序：");
  Traversal.postOrder();
  Traversal.postOrderRecursion(Traversal.createBinTree());
 }
}

/**
 * 节点数据结构
 *
 * @author bin.zhang
 * @version 2017年8月30日 上午11:49:38
 */
class BinTreeNode {

 BinTreeNode() {
 }

 BinTreeNode(char data, int flag, BinTreeNode lchild, BinTreeNode rchild) {
  this.data = data;
  this.flag = flag;
  this.lchild = lchild;
  this.rchild = rchild;
 }

 char data;
 int flag;
 BinTreeNode lchild, rchild;

}

class Traversal {

 /**
  * 创建一棵二叉树
  *
  * @author bin.zhang
  * @return 根节点
  */
 public static BinTreeNode createBinTree() {
  BinTreeNode R3 = new BinTreeNode('F', 0, null, null);
  BinTreeNode L2 = new BinTreeNode('D', 0, null, null);
  BinTreeNode R2 = new BinTreeNode('E', 0, null, R3);
  BinTreeNode L1 = new BinTreeNode('B', 0, L2, R2);
  BinTreeNode R1 = new BinTreeNode('C', 0, null, null);
  BinTreeNode T = new BinTreeNode('A', 0, L1, R1);
  return T;
 }

 // 前序
 public static void preOrder() {

  BinTreeNode p = createBinTree();

  Stack<BinTreeNode> stack = new Stack<BinTreeNode>();

  while (p != null || !stack.empty()) {
   if (p != null) {
    System.out.print(p.data);
    stack.push(p);
    p = p.lchild;
   }
   else {
    p = stack.pop();
    p = p.rchild;
   }
  }
  System.out.println();

 }

 // 前序递归
 public static void preOrderRecursion(BinTreeNode top) {
  if (top != null) {
   System.out.println(top.data);
   preOrderRecursion(top.lchild);
   preOrderRecursion(top.rchild);
  }
 }

 // 中序
 public static void inOrder() {

  BinTreeNode p = createBinTree();

  Stack<BinTreeNode> stack = new Stack<BinTreeNode>();

  while (p != null || !stack.empty()) {
   if (p != null) {
    stack.push(p);
    p = p.lchild;
   }
   else {
    p = stack.pop();
    System.out.print(p.data);
    p = p.rchild;
   }
  }
  System.out.println();
 }

 // 中序递归
 public static void inOrderRecursion(BinTreeNode top) {
  if (top != null) {
   inOrderRecursion(top.lchild);
   System.out.println(top.data);
   inOrderRecursion(top.rchild);
  }
 }

 // 后序
 public static void postOrder() {

  BinTreeNode p = createBinTree();

  Stack<BinTreeNode> stack = new Stack<BinTreeNode>(); // 初始化栈

  int mark = 1; // 转向标志
  while (p != null || !stack.empty()) { // 遍历
   if (p != null && mark != 0) {
    stack.push(p);
    p = p.lchild;
   }// 转向左子树
   else {
    p = stack.pop();
    p.flag++; // 退栈
    if (p.flag == 1) {
     stack.push(p);
     p = p.rchild;
     mark = 1;
    } // 转向右子树
    else if (p.flag == 2 && !stack.empty()) { // 输出结点
     System.out.print(p.data);
     mark = 0;
    }
    else if (p.flag == 2 && stack.empty()) { // 输出根结点并退出
     System.out.print(p.data);
     break;
    }
   } // if-else
  } // while
  System.out.println();
 }

 // 后序递归
 public static void postOrderRecursion(BinTreeNode top) {
  if (top != null) {
   postOrderRecursion(top.lchild);
   postOrderRecursion(top.rchild);
   System.out.println(top.data);
  }
 }
}

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。