DSP中浮点转定点运算--浮点数的存储格式

二：浮点数的存储格式

2.1 IEEE floating point standard

　　上面我们说了，浮点数的小数点是不固定的，如果每个人都按照自己的爱好存储在电脑里，那不就乱套了吗？那么怎么在计算机中存储这种类型的数字呢？象这类古老的问题前人早都为我们做好了相应的规范，无规矩不成方圆吗。我们平时所说的浮点数的存储规范，就是由IEEE指定的，具体的规范文件是：IEEE Standard 754 for Binary Floating-Point Arithmetic。大家可以很容易的从网络上下载到这篇文档。

　　在c语言中，单精度（float）数据类型为32bits，具体的如下图所示：

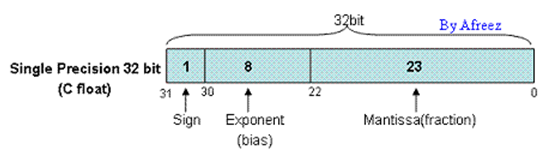
整个32bits分三部分，即

　　Sign：符号位，1 bit，0为正，1为负；

　　Exponent(bias)：指数部分，8 bits，存储格式为移码存储（后面还会说明），偏移量为127；

　　Mantissa(fraction)：尾数部分。

　　对应的双精度（double）类型的格式为：

同样，64位也被分为了三部分，对照单精度，不用我说就可以理解各个部分的含义了吧？

　　是不是有点迷糊了，不要怕，理论这个东西最能忽悠人了，看起来很高深，其实也就是个屁大的事，举个例子就很容易明白了。

举例说明，如3.24x103，则对应的部分为，Sign为0，3为指数部分（注意计算机里面存储的不是3，这里仅仅为了说明），3.24为尾数。我们知道，计算机“笨”的要死，只认识0和1，那么到底一个浮点数值在计算机存储介质中是如何存储的呢？

例如，我们要想偷窥浮点类型的值4.25在计算机硬盘中存储的庐山真面目，请跟我来：首先把4.25转换成二进制的表达方式，即100.01，在详细点，变成1.0001x22，好了，对号入座把。

Sign=0;

Exponent(bias)=2+127=129 （偏移量为127，就是直接加上个127了）；

Mantissa=1.0001-1.0=0001（规格化后，小数点前总是整数1，全世界人都知道前面是1不是0，所以省略不写了，即尾数部分不包括整数部分；当别人问你，为什么23 bit的尾数部分可以表示24位的精度，知道怎么回答了吧。 靠，什么，没有看懂，再仔细读两便就知道了）。

对照上面的图示，相信你已经看明白了吧？相信你的智商。为了加深认识，再来一个。如果给定你一个二进制数字串，01000000100010000000000000000000，并告诉你这是一个float类型的值，让你说出它是老几，知道怎么算了吧？如果不知道，看下面的图，我就不废话解释了。

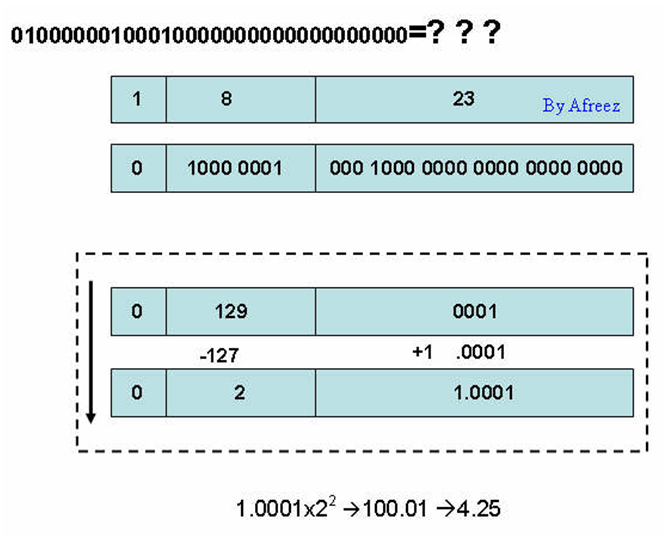
2．2深入理解浮点存储格式

为了更深入的理解浮点数的格式。我们使用C语言来做一件事。在C语言的世界里，强制类型转换，大家应该都很熟悉了。例如：

代码如下:

…

float f=4.6;

int i;

…

i = (int)(f+0.5); // i=5

..

下面我们不使用强制类型转化，我们自己来计算f转换成整形应该等于几？

把主要代码帖出来，如下：

代码如下:

//取23+1位的尾数部分

int ival= ((*(int *)(&fval)) & 0x07fffff) | 0x800000;

// 提取指数部分

int exponent = 150 - (((*(int *)(&fval)) >> 23) & 0xff);

if (exponent < 0)

ival = (ival<< -exponent);

else

ival = (ival >> exponent);

// 如果小于0，则将结果取反

if ((*(int *)&fval) & 0x80000000)

ival = -ival;

好好琢磨琢磨吧，看明白了，就说明你基本明白了浮点数的存储格式，如果没有看明白，接着看，知道明白为止。

以上就是本文的全部内容，希望能给大家一个参考，也希望大家多多支持我们。

赞 (0)

相关推荐

  • DSP中浮点转定点运算--举例及编程中的心得

    5．举例及编程中的心得 5．1举例 "第3章  DSP芯片的定点运算.doc"这篇文章中给了一个很简单有能说明问题的例子,不想动大脑了,直接引用过来如下. 这是一个对语音信号(0.3kHz~3.4kHz)进行低通滤波的C语言程序,低通滤波的截止频率为800Hz,滤波器采用19点的有限冲击响应FIR滤波.语音信号的采样频率为8kHz,每个语音样值按16位整型数存放在insp.dat文件中. 例3.7  语音信号800Hz 19点FIR低通滤波C语言浮点程序 复制代码 代码如下: #inc

  • DSP中浮点转定点运算--定点数的加减乘除运算

    3.定点数的加减乘除运算 简单的说,各种运算的原则就是先把待运算的数据放大一定的倍数,在运算的过程中使用的放大的数据,在最终需要输出结果的时候再调整回去. 举个例来说,有如下运算: 复制代码 代码如下: - // coefs1 = 0.023423; coefs2=0.2131 float coefs1,coefs2; int result; - result = 34* coefs1+72* coefs2; - 代码的意思是,该模块需要输出一个整型的结果,但计算的过程中有浮点的运算.如果在定点

  • 深入C/C++浮点数在内存中的存储方式详解

    任何数据在内存中都是以二进制的形式存储的,例如一个short型数据1156,其二进制表示形式为00000100 10000100.则在Intel CPU架构的系统中,存放方式为  10000100(低地址单元) 00000100(高地址单元),因为Intel CPU的架构是小端模式.但是对于浮点数在内存是如何存储的?目前所有的C/C++编译器都是采用IEEE所制定的标准浮点格式,即二进制科学表示法.在二进制科学表示法中,S=M*2^N 主要由三部分构成:符号位+阶码(N)+尾数(M).对于flo

  • 浮点数在计算机中存储方式是怎样的

    浮点数在计算机中存储方式是怎样的

    C语言和C#语言中,对于浮点类型的数据采用单精度类型(float)和双精度类型(double)来存储,float数据占用32bit,double数据占用64bit,我们在声明一个变量float f= 2.25f的时候,是如何分配内存的呢?如果胡乱分配,那世界岂不是乱套了么,其实不论是float还是double在存储方式上都是遵从IEEE的规范的,float遵从的是IEEE R32.24 ,而double 遵从的是R64.53. 无论是单精度还是双精度在存储中都分为三个部分: 1.符号位(Sign

  • DSP中浮点转定点运算--浮点与定点概述

    一:浮点与定点概述 1.1相关定义说明 定点数:通俗的说,小数点固定的数.以人民币为例,我们日常经常说到的如123.45￥,789.34￥等等,默认的情况下,小数点后面有两位小数,即角,分.如果小数点在最高有效位的前面,则这样的数称为纯小数的定点数,如0.12345,0.78934等.如果小数点在最低有效位的后面,则这样的数称为纯整数的定点数,如12345,78934等. 浮点数:一般说来,小数点不固定的数.比较容易的理解方式是,考虑以下我们日常见到的科学记数法,拿我们上面的数字举例,如123.

  • DSP中浮点转定点运算--定点数模拟浮点数运算及常见的策略

    4.定点数模拟浮点数运算及常见的策略 相信大家到现在已经大致明白了浮点数转换成定点数运算的概貌.其实,原理讲起来很简单,真正应用到实际的项目中,可能会遇到各种各样的问题.具我的经验,常见的策略有如下几条: 1)除法转换为乘法或移位运算 我们知道,不管硬件平台如果变换,除法运算所需要的时钟周期都远远多于乘法运算和加减移位运算,尤其是在嵌入式应用中,"效率"显得尤为重要.以笔者的经验,其实,项目中的很大一部分除法运算是可以转换成乘法和移位运算,效率还是有很大提升空间的. 2)查表计算 有些

  • DSP中浮点转定点运算--浮点数的存储格式

    DSP中浮点转定点运算--浮点数的存储格式

    二:浮点数的存储格式 2.1 IEEE floating point standard 上面我们说了,浮点数的小数点是不固定的,如果每个人都按照自己的爱好存储在电脑里,那不就乱套了吗?那么怎么在计算机中存储这种类型的数字呢?象这类古老的问题前人早都为我们做好了相应的规范,无规矩不成方圆吗.我们平时所说的浮点数的存储规范,就是由IEEE指定的,具体的规范文件是:IEEE Standard 754 for Binary Floating-Point Arithmetic.大家可以很容易的从网络上下载

  • PHP中两个float(浮点数)比较实例分析

    本文实例讲述了PHP中两个float(浮点数)比较方法.分享给大家供大家参考.具体如下: 最近在开发一个合同管理系统的时候,涉及到两个浮点数比较,算是把我郁闷惨了. 在N久以前,就不晓得从哪里听来的一个"不要用等号去比较浮点数"的"真理",自己平时也在用,好像没有出现啥问题,可这次问题总算是来了. <?php $sum = "12300.00"; $a = "10000.30"; $b = "2000.30&q

  • PHP中round()函数对浮点数进行四舍五入的方法

    本文实例讲述了PHP中round()函数对浮点数进行四舍五入的方法.分享给大家供大家参考.具体方法如下: 语法:round(x,prec) 参数 描述 x 可选,规定要舍入的数字. prec 可选,规定小数点后的位数. 说明:返回将 x 根据指定精度 prec(十进制小数点后数字的数目)进行四舍五入的结果,prec 也可以是负数或零(默认值). 提示和注释 注释:php默认不能正确处理类似 "12,300.2" 的字符串. 注释:prec 参数是在 php 4 中被引入的,实例代码如下

  • python中实现精确的浮点数运算详解

    为什么说浮点数缺乏精确性? 在开始本文之前,让我们先来谈谈浮点数为什么缺乏精确性的问题,其实这不是Python的问题,而是实数的无限精度跟计算机的有限内存之间的矛盾. 举个例子,假如说我只能使用整数(即只精确到个位,计算机内的浮点数也只有有限精度,以C语言中的双精度浮点数double为例,精度为52个二进制位),要表示任意实数(无限精度)的时候我就只能通过舍入(rounding)来近似表示. 比如1.2我会表示成1,2.4表示成2,3.6表示成4. 所以呢? 在算1.2 - 1.2的时候,由于计

  • python中精确输出JSON浮点数的方法

    有时需要在JSON中使用浮点数,比如价格.坐标等信息.但python中的浮点数相当不准确, 例如下面的代码: 复制代码 代码如下: #!/usr/bin/env python import json as json data = [ 0.333, 0.999, 0.1 ]print json.dumps(data) 输出结果如下: 复制代码 代码如下: $ python floatjson.py[0.33300000000000002, 0.999, 0.10000000000000001] 能

  • Java中使用BigDecimal进行浮点数运算

    最近研究了一下Java的浮点数计算问题,从网上查询了相关的资料,汇总并经过了一些整理和调试,最后完成此文,欢迎大家指出其中的错误和问题. 在Java中,float声明的变量是单精度浮点数,double声明的变量是双精度浮点数,顾名思义就是double型的实体占用内存空间是float的两倍.float是4个字节而double是8个字节.float和double类型的数据,无法精确表示计算结果,这是由于float和double是不精确的计算.大家可以通过下面代码可以看出来: 复制代码 代码如下: p

随机推荐