Python线性回归实战分析

一、线性回归的理论

1）线性回归的基本概念

线性回归是一种有监督的学习算法，它介绍的自变量的和因变量的之间的线性的相关关系，分为一元线性回归和多元的线性回归。一元线性回归是一个自变量和一个因变量间的回归，可以看成是多远线性回归的特例。线性回归可以用来预测和分类，从回归方程可以看出自变量和因变量的相互影响关系。
线性回归模型如下：

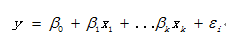
对于线性回归的模型假定如下：
（1） 误差项的均值为0，且误差项与解释变量之间线性无关

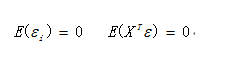
（2） 误差项是独立同分布的，即每个误差项之间相互独立且每个误差项的方差是相等的。

（3） 解释变量之间线性无关

（4） 正态性假设，即误差项是服从正态分布的

以上的假设是建立回归模型的基本条件，所以对于回归结果要进行一一验证，如果不满足假定，就要进行相关的修正。

2) 模型的参数求解

（1）矩估计

一般是通过样本矩来估计总体的参数，常见是样本的一阶原点矩来估计总体的均值，二阶中心矩来估计总体的方差。

（2）最小二乘估计

一般最小二乘估计是适用于因变量是连续型的变量，最常用的是普通最小二乘法（ Ordinary Least Square，OLS），它的原理是所选择的回归模型应该使所有观察值的残差平方和达到最小。预测值用 表示，对应的实际值 ，残差平方和 ，最小二乘估计是求得参数的值，使得L最小。对于线性回归求得的参数值是唯一的。

（3）极大似然估计

极大似然估计是基于概率的思想，它要求样本的概率分布是已知的，参数估计的值是使得大量样本发生的概率最大，用似然函数来度量，似然函数是各个样本的密度函数的乘积，为方便求解对其求对数，加负号求解极小值，得到参数的估计结果。

3）模型的优缺点

优点：结果易于理解，计算上不复杂

缺点：对于非线性的数据拟合不好

二、用Python实现线性回归的小例子

数据来源于网络爬虫，武汉市商品房价格为因变量和几个相关关键词的百度指数的搜索量为自变量。

由于本文的自变量有98个，首先进行自变量的选择，先是通过相关系数矩阵筛选掉不相关的变量，根据Pearson相关系数矩阵进行变量的选取，一般选取相关系数的值大于0.3的变量进行回归分析，由于本文的变量较多，先进行手动筛选然后利用相关系数进行选取，本文选取相关系数大于0.55的变量进行回归分析。

经过相关系数的分析选取8个变量进行下一步的分析，分析的Python代码如下：

# -*- coding: utf-8 -*-
#### Required Packages
import sys
reload(sys)
sys.setdefaultencoding('utf-8')
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import statsmodels.api as sm
data = pd.read_csv('Hdata.csv')
print data
dataset = np.array(data)
######相关性分析
X = dataset[:,1:98]
y = dataset[:,0]
cor = np.corrcoef(dataset,rowvar=0)[:,0]
######输出相关矩阵的第一列
print cor
#######筛选后的数据读取
data1 = pd.read_csv('H1data.csv')
dataset1 = np.array(data)
######筛选后的变量######
X1 = dataset1[:,1:8]
Y1 = dataset1[:,0]
est = sm.OLS(Y1,X1).fit()
print est.summary()

贴出线性回归的结果如下：

OLS RegressionResults
=======================================================================
Dep. Variable:           y  R-squared:            0.978
Model:              OLS  Adj. R-squared:         0.974
Method:         Least Squares F-statistic:          287.5
Date:        Sat, 08 Apr 2017  Prob (F-statistic):      9.35e-36
Time:            15:15:14  Log-Likelihood:        -442.82
No. Observations:         53  AIC:               899.6
Df Residuals:           46  BIC:               913.4
Df Model:              7
Covariance Type:      nonrobust
=======================================================================
         coef  std err     t   P>|t|   [95.0% Conf. Int.]
-----------------------------------------------------------------------
x1      -0.3691   0.494  -0.747   0.0459    -1.364   0.626
x2       0.3249   0.353   0.920   0.0362    -0.386   1.036
x3       1.0987   0.837   1.312   0.0196    -0.587   2.784
x4       0.7613   0.790   0.964   0.0340    -0.829   2.351
x5      -1.5766   1.099  -1.435   0.0158    -3.789   0.636
x6      -0.1572   1.077  -0.146   0.0885    -2.325   2.011
x7       3.2003   1.603   1.997   0.052    -0.026   6.427
=======================================================================
Omnibus:            0.413  Durbin-Watson:          1.748
Prob(Omnibus):         0.814  Jarque-Bera (JB):        0.100
Skew:              0.097  Prob(JB):            0.951
Kurtosis:            3.089  Cond. No.             95.5
=======================================================================

从回归分析的结果可以看出来，模型的拟合优度R-squared=0.978，说明模型的拟合效果很好，据其大小对拟合效果的优劣性进行判定。对模型整体的显著性可以通过F统计量来看，结果显示的F统计量对应的P值显著小于0.05（0.05是显著性水平,也可以选取0.01），说明模型整体是显著的，它的显著性说明被解释变量能不能由这些解释变量进行解释，F检验是对整体的检验，F检验的通过不代表每一个解释变量是显著的。对每一个变量的显著性要看t检验统计量的值，t检验统计量对应的P值小于0.05（0.01或者0.1也行，具体看情况分析，一般选取0.05）视为是显著的，从结果可以看出，X6和X7的变量的p是大于0.05的，也就是这两个变量对被解释变量的影响是不显著的要剔除。但是如果你只是关心预测的问题那么可以不剔除。但是如果有研究解释变量对被解释变量的影响的程度的，要做进一步的研究。接下来看DW的值，DW的值为1.748，说明模型不存在自相关性。看JB检验统计量的值，JB检验统计量是对正态性的假设进行检验的，JB的值对应的p值为0.951显著大于0.05，可以认为模型满足正态性的假设的。对于参数的实际意义本文就不做解释了。

对于DW值判断相关性的依据如下：

DW=0时，残差序列存在完全正自相关，

DW=（0，2）时，残差序列存在正自相关，

DW=2时，残差序列无自相关，

DW=（2，4）时，残差序列存在负自相关，

DW=4时，残差序列存在完全负自相关。

对于建立模型的一般步骤简单描述如下：

（1） 根据数据的表现形式选取合适的模型

（2） 对选取的模型选取适用的参数估计方法

（3） 对参数的结果进行检验

（4） 对结果进行解释

您可能感兴趣的文章:

• Python编程实现线性回归和批量梯度下降法代码实例
• Python数据拟合与广义线性回归算法学习
• Python编程实现使用线性回归预测数据
• python编程线性回归代码示例
• Python scikit-learn 做线性回归的示例代码