R语言实现KMeans聚类算法实例教程

目录

• 什么是k-means聚类算法
• R 实现kmeans聚类算法
• 加载包
• 加载示例数据
• 寻找最佳聚类数量
• 使用最优k执行kmeans聚类
• kmeans 算法的优缺点
• 总结

本文和你一起学习无监督机器学习算法 ———— kmeans算法，并在R中给详细的实现示例和步骤。

什么是k-means聚类算法

聚类是从数据集中对观测值进行聚类的机器学习方法。它的目标是聚类相似观测值，不同类别之间差异较大。聚类是一种无监督学习方法，因为它仅尝试从数据集中发现结构，而不是预测应变量的值。

下面是一个市场营销中对客户分类的场景，通过下面客户信息：

• 家庭收入
• 住房面积
• 户主职业
• 据城区距离

我们利用这些信息进行聚类，可识别相似家庭，从而能够识别某类型家庭可能购买某种产品或对某种类型的广告反应更好。

最常用的聚类算法就是k-means聚类算法，下面我们介绍k-means算法并通过示例进行说明。

k-means聚类算法把数据集中每个观测值分为K个类别。每个分类中的观测值相当类似，K类之间彼此差异较大。实际应用中执行下列几步实现k-means聚类算法：

1.确定K值

首先确定把数据集分为几类。通常我们简单测试几个不同值K，然后分析结果，确定那个值更有现实意义。

2.将每个观察结果随机分配到一个初始簇中，从1到K。

3.执行以下步骤，直到集群分配停止变化。

对于K个集群中的每一个，计算集群的质心。这仅仅是第k个簇中观测的p特征的向量。

将每个观测值分配到质心最近的簇中。在这里最接近的是用欧氏距离来定义的。

下面通过示例展示R的实现过程。

R 实现kmeans聚类算法

加载包

首先加载两个包，包括kmeans算法的一些辅助函数。

library(factoextra)
library(cluster)

加载示例数据

对于本例我们将使用R中内置的usarrest数据集，该数据集包含1973年美国每个州每10万居民因谋杀、袭击和强奸而被捕的人数，以及每个州居住在城市地区的人口百分比(UrbanPop)。

#load data
df <- USArrests

#remove rows with missing values
df <- na.omit(df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

#                Murder   Assault   UrbanPop         Rape
# Alabama    1.24256408 0.7828393 -0.5209066 -0.003416473
# Alaska     0.50786248 1.1068225 -1.2117642  2.484202941
# Arizona    0.07163341 1.4788032  0.9989801  1.042878388
# Arkansas   0.23234938 0.2308680 -1.0735927 -0.184916602
# California 0.27826823 1.2628144  1.7589234  2.067820292
# Colorado   0.02571456 0.3988593  0.8608085  1.864967207

上面代码首先加载USArrests数据集，删除缺失值，对数据值进行标准化。

寻找最佳聚类数量

执行kmeans聚类算法，我们可以使用内置包stat中的kmeans()函数，语法如下：

kmeans(data, centers, nstart)

• data : 数据集名称
• centers: 聚类数量,即选择k的值
• nstart: 初始配置个数。因为不同的初始启动集合可能会导致不同的结果，所以建议使用几种不同的初始配置。k-means算法将找到导致簇内变异最小的初始配置。

既然在使用kmeans函数之前并不确定最优聚类数量，下面通过两个图来辅助我们决定：

1.聚类数量 vs. 总体平方和

首先使用 fviz_nbclust 函数创建一个图，展示聚类数量及总体平方和之间的关系：

fviz_nbclust(df, kmeans, method = "wss")

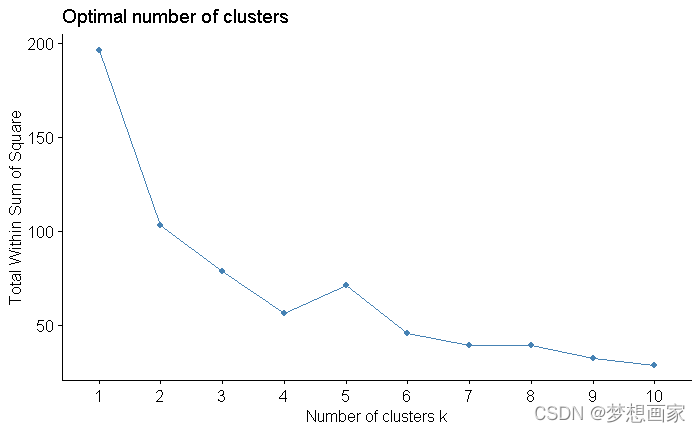
通常我们创建这类图形寻找某个K类对应的平方和值开始弯曲或趋于平缓的肘形。这通常是最理想的聚类数量。上图中显然在k = 4个时出现肘形。

2.聚类数量 vs. 差距统计

另一个决定最佳聚类数量的是使用指标：差距统计。它用于比较不同k值聚类差距变化情况。使用cluster包中的clusGap()以及fviz_gap_stat()函数画图：

#calculate gap statistic based on number of clusters
gap_stat <- clusGap(df,
                    FUN = kmeans,
                    nstart = 25,
                    K.max = 10,
                    B = 50)

#plot number of clusters vs. gap statistic
fviz_gap_stat(gap_stat)

从上图可以看到k=4时，差距统计最大，这与前面图的结果一致。

使用最优k执行kmeans聚类

最后，我们执行kmeans函数，使用k=4作为最优值：

# 设置随机种子，让结果可以重现
set.seed(1)

# 调用kmeans聚类算法 k = 4
km <- kmeans(df, centers = 4, nstart = 25)

# 查看结果
km

# Show in New Window
# Clustering k = 1,2,..., K.max (= 10): .. done
# Bootstrapping, b = 1,2,..., B (= 50)  [one "." per sample]:
# .................................................. 50
# R Console
#
#
# Show in New Window
# K-means clustering with 4 clusters of sizes 13, 13, 16, 8
#
# Cluster means:
#       Murder    Assault   UrbanPop        Rape
# 1 -0.9615407 -1.1066010 -0.9301069 -0.96676331
# 2  0.6950701  1.0394414  0.7226370  1.27693964
# 3 -0.4894375 -0.3826001  0.5758298 -0.26165379
# 4  1.4118898  0.8743346 -0.8145211  0.01927104
#
# Clustering vector:
#        Alabama         Alaska        Arizona       Arkansas     California       Colorado
#              4              2              2              4              2              2
#    Connecticut       Delaware        Florida        Georgia         Hawaii          Idaho
#              3              3              2              4              3              1
#       Illinois        Indiana           Iowa         Kansas       Kentucky      Louisiana
#              2              3              1              3              1              4
#          Maine       Maryland  Massachusetts       Michigan      Minnesota    Mississippi
#              1              2              3              2              1              4
#       Missouri        Montana       Nebraska         Nevada  New Hampshire     New Jersey
#              2              1              1              2              1              3
#     New Mexico       New York North Carolina   North Dakota           Ohio       Oklahoma
#              2              2              4              1              3              3
#         Oregon   Pennsylvania   Rhode Island South Carolina   South Dakota      Tennessee
#              3              3              3              4              1              4
#          Texas           Utah        Vermont       Virginia     Washington  West Virginia
#              2              3              1              3              3              1
#      Wisconsin        Wyoming
#              1              3
#
# Within cluster sum of squares by cluster:
# [1] 11.952463 19.922437 16.212213  8.316061
#  (between_SS / total_SS =  71.2 %)
#
# Available components:
#
# [1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
# [6] "betweenss"    "size"         "iter"         "ifault"

从结果可见：

• 16 州分在第一个类
• 13 州分在第二个类
• 13 州分在第三个类
• 8 州分在第四个类

我们可以通过fviz_cluster()函数在二维空间中以散点图方式展示结果：

#plot results of final k-means model
fviz_cluster(km, data = df)

也可以使用aggregate()函数查看每个类中变量的均值：

#find means of each cluster
aggregate(USArrests, by=list(cluster=km$cluster), mean)

# cluster	  Murder   Assault	UrbanPop	    Rape
#
# 1	3.60000	  78.53846	52.07692	12.17692
# 2	10.81538 257.38462	76.00000	33.19231
# 3	5.65625	 138.87500	73.87500	18.78125
# 4	13.93750 243.62500	53.75000	21.41250

输出结果解释如下：

• 在第一类中的州中平均每100,000人谋杀数为 3.6
• 在第一类中的州中平均每100,000人袭击数为 78.5
• 在第一类中的州中平均每100,000人城区居民率为 52.1%
• 在第一类中的州中平均每100,000人强奸数为 3.6 12.2

最后我们把聚类结果附加到原始数据集中：

#add cluster assigment to original data
final_data <- cbind(USArrests, cluster = km$cluster)

#view final data
head(final_data)

# 	    Murder	Assault	UrbanPop  Rape	 cluster
#
# Alabama	    13.2	236	58	  21.2	 4
# Alaska	    10.0	263	48	  44.5	 2
# Arizona	     8.1	294	80	  31.0	 2
# Arkansas     8.8	190	50	  19.5	 4
# California   9.0	276	91	  40.6	 2
# Colorado     7.9	204	78	  38.7	 2

kmeans 算法的优缺点

优点：

很快的算法能够处理大数据集

缺点：

在执行算法之前需要指定聚类数量对异常值敏感 总结

本文我们讨论了kmeans算法的概念，并在R中给详细实现示例和步骤。

总结

到此这篇关于R语言实现KMeans聚类算法教程的文章就介绍到这了,更多相关R语言KMeans聚类算法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！