基于np.arange与np.linspace细微区别(数据溢出问题)

目录

• 太长不看的简洁版本
• 问题前夕
• 我的代码
• 同门的代码
• 代码对比【区别只体现在自变量x】
• 官方API解析
• 解决办法

太长不看的简洁版本

1.x = np.arange(start, end, steps)

Values are generated within the half-open interval [start, stop)
(in other words, the interval including start but excluding stop).

• 即区间是左闭右开的，不包含end的取值

2.x = np.linspace(start, end, num, endpoint=True)

There are num equally spaced samples in the closed interval [start, stop] or the half-open interval [start, stop) (depending on whether endpoint is True or False).

• 即endpoint=True区间是左闭右闭的，包含end的取值
• 即endpoint=False区间是左闭右开的，不包含end的取值

最终结论：

• 当linspace函数指定参数endpoint=False时，两个函数的效果等价。
• 当steps和num指定参数都是整数时，arrange会返回numpy.int32数据类型，
• 而linspace会返回numpy.float数据类型，对应于 C 语言数据类型，每种“整数”有自己的区间，会遇到数据溢出的问题，数值分析中函数绘制曲线将得不到正确的答案。

解决方案：

• 使用 np.linspace比np.arange好，可以预防数据溢出的问题
• 使用np.arange时，将步长steps设置为小数，比如1.0

绘制曲线代码：

x = np.arange(0,100,1.0)                           #自变量的范围
x = np.linspace(0, 100, 100，endpoint=False)       # 两者效果等价
y = alpha*(T-x) + beta*(T**4-x**4) + gamma*(u**2)  #因变量
plt.plot(x, y, y*0.0)                              #曲线绘制

问题前夕

数值分析课程作业用python的matplotlib一直得不到正确的曲线图，后用Matlab就可以，明明是一样的函数，但是两者绘制出来的曲线图显示零点不一致，差距很大。

作为一枚不会matlab的学渣，为了得到正确的答案，难道真的必须啃下matlab的语法吗…又问了一下同门，他居然用python得出了正确的答案，排查两个小时一无所获转战Matlab的我留下了羡慕的泪水，赶紧要来了他的代码进行对比实验，终于找出了问题的关键了，预知后事如何请继续往下看…

我的代码

u = 21.0
T = 293.15
alpha = 50.0
beta = 2*(10**(-7))
gamma = 800.0
x = np.arange(0,10000,1)                           #自变量的范围
y = alpha*(T-x) + beta*(T**4-x**4) + gamma*(u**2)  #因变量
plt.plot(x, y, y*0.0)

效果图

从图中可以看出函数的零点在[7000,8000]这个范围。

那么问题来了，为什么表达式不是一次函数绘制出来的图形却是一条直线，x^4怎么也不能是一条直线吧？？？带着这个疑惑，我找了同学要了他的答案来对照，发现零点只有一个，在[1000,1200]这个范围内。我仔细对照了函数方程，苦苦思索了两个小时也没找到答案。

同门的代码

u = 21.0
T = 293.15
alpha = 50.0
beta = 2*(10**(-7))
gamma = 800.0
start = 1000
end = 1500
step = 1
num = (end - start) // step
x = np.linspace(start, end, num)
y = alpha*(T-x) + beta*(T**4-x**4) + gamma*(u**2)
fig = plt.figure(figsize=(6, 6))
plt.plot(x, y, label='Numerical Analysis')
plt.grid(True)
plt.xlim((800, 1500))  # 显示的x的范围（不设置则由程序自动设置）
plt.ylim((-10, 10))  # 显示的y的范围
plt.legend()           # 显示旁注
plt.show(fig)          # 没有输入值默认展示所有对象

效果图

从图中可以看出同门的代码跑出来的结果是正确的，并且这条线还是弯的…我以为是plt叠加导致的buff加成，然后我把作图的代码copy到我的代码里，仍然是错误的！！！在逐步分析后，我发现导致这个现象的原因居然只是一行代码的差距！！！展示如下：

代码对比【区别只体现在自变量x】

u = 21.0
T = 293.15
alpha = 50.0
beta = 2*(10**(-7))
gamma = 800.0
x = np.arange(1000,1500,1)           #区别只体现在自变量x所用的函数
#x = np.linspace(1000, 1500, 500)    #区别只体现在自变量x所用的函数
y = alpha*(T-x) + beta*(T**4-x**4) + gamma*(u**2)
plt.plot(x, y)

x = np.arange(1000,1500,1)的效果图

[<matplotlib.lines.Line2D at 0x29e40ceff10>]

x = np.linspace(1000, 1500, 500)的效果图

[<matplotlib.lines.Line2D at 0x29e40da97c0>]

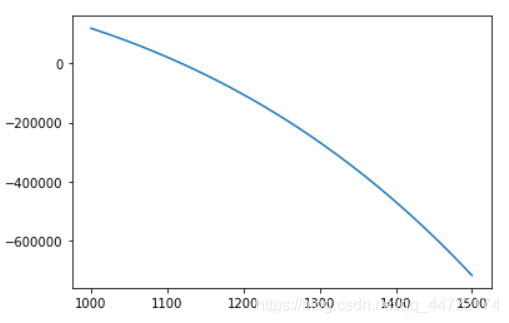
x = np.arange(1000,1500,0.1)的效果图

咦，此时我不禁疑惑，我使用的np.arange也是1000-1500，以1为间隔，自变量取值为

[1000, 1001, 1002，…, 1499]

使用的np.linspace也是把1000-1500切分为500份，

[1000, 1001.00200401, 1002.00400802, …, 1498.99799599, 1500]

效果理应是差不多的。

但是为什么我用arange函数的时候需要将精度设为0.1，才能实现linspace精度为1的效果呢？？？

官方API解析

x = np.arange(0,10,1)
#输出： [0 1 2 3 4 5 6 7 8 9]
x1 = np.linspace(0, 10, 10, endpoint=False)
#输出：[0. 1. 2. 3. 4. 5. 6. 7. 8. 9.]
x1 = np.linspace(0, 10, 10)
#输出：[ 0.          1.11111111  2.22222222  3.33333333  4.44444444  5.55555556
  6.66666667  7.77777778  8.88888889 10.        ]

上面的例子表明：当指定endpoint为False时，两个函数的效果等价。此时，我似乎发现了一点不对劲，一个输出的是整数，一个输出的是小数？？？会不会这个对结果造成了影响呢？怀着想都不敢想的梦想，我尝试了一下将整数设置为浮点数…

x = np.arange(1000,1500,1.0)的效果图

我的天呀，居然把取样间隔从1设置为1.0效果居然有这么大的不同，此时我的疑惑非但没有减轻，反而更加疑惑了，整数和浮点数作图效果的天差地别，又是什么原因导致的呢？我想了想，毕竟我学的这门课叫做《数值分析》啊，那我毕竟也得有点这方面的一点见解？…也许这个表达式太过于复杂，整数输进去再经过七七七八八的加减乘除后，自变量为整型+1、-1差别很细微可以忽略不计。最主要是我的因变量的范围是10^5，微小的变化也许体现不出来？？？但是我的常量设置的时候特地全都设置为浮点数了。

通过MATLAB已知零点在[1118,1119]之间，我特地打印出x=1118和x=1119对应因变量的值：

x1 = 1118;      #对应因变量y=572.5297745541902
x2 = 1119;      #对应因变量y=-596.9030544458074
x = np.arange(1110,1120,1.0)  

输出：

[9820.44892975 8674.86472155 7526.31814255 6374.80385755 5220.31652655
 4062.85080475 2902.40134255 1738.96278555  572.52977455 -596.90305445]
x = np.arange(1110,1120,1)

输出：

[313045.14002735 313617.54273755 313327.98961775 313035.46879195
 313598.96837935 313300.49611675 312999.04011375 312694.59501595
 313246.14892335 312935.70955355]

由x1，x2可以看出零点确实在这个范围内，但是自变量为整型时，很有可能是溢出了，导致计算值与真实值天差地别。不但正数数值不对，而且零点也消失了。但是我单独输入1119也是整型，为什么可以得到正确值？python最新版本对整型没有限制了，原来能表示的最大整型为9223372036854775807。Numpy 中的整数类型对应于 C 语言的数据类型，每种“整数”有自己的区间，要解决数据溢出问题，需要指定更大的数据类型（dtype）！！！

原来我单独输入x的值，此时用的是python的版本表示的整型，是源码里自带了溢出防止办法，所以函数值能正确输出，但是x = np.arange(1110,1120,1)，对应的每一个自变量的类型输出为：

<class ‘numpy.int32’>

只能表示数据范围整数（-2147483648 to 2147483647），当x取值为10^3时，对应四次方结果为1000000000000，已经超出可以表示的范围了。到这里已经把我的坑解释的很清楚了。

解决办法

大家以后要作图绘制曲线最好使用np.linspace，会自动把自变量取值设置为浮点型，或者np.arange(start,end,1.0)，步长设置为浮点型！！！这样的话才不会出现溢出等问题！！！！

花了半天的时间终于把这个坑给解决了，给自己

以上为个人经验，希望能给大家一个参考，也希望大家多多支持我们。