Python深度学习pytorch神经网络图像卷积运算详解

目录
  • 互相关运算
  • 卷积层
  • 特征映射

由于卷积神经网络的设计是用于探索图像数据，本节我们将以图像为例。

互相关运算

严格来说，卷积层是个错误的叫法，因为它所表达的运算其实是互相关运算（cross-correlation），而不是卷积运算。在卷积层中，输入张量和核张量通过互相关运算产生输出张量。

首先，我们暂时忽略通道（第三维）这一情况，看看如何处理二维图像数据和隐藏表示。下图中，输入是高度为3、宽度为3的二维张量（即形状为 3 × 3 3\times3 3×3）。卷积核的高度和宽度都是2。

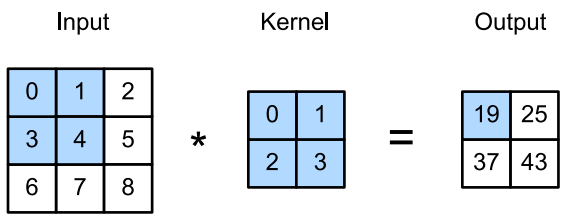
注意，输出大小略小于输入大小。这是因为我们需要足够的空间在图像上“移动”卷积核。稍后，我们将看到如何通过在图像边界周围填充零来保证有足够的空间移动内核，从而保持输出大小不变。

def corr2d(X, K):
	"""计算⼆维互相关运算。"""
	h, w = K.shape
	Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
	for i in range(Y.shape[0]):
		for j in range(Y.shape[1]):
			Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
	return Y

卷积层

卷积层对输入和卷积核权重进行互相关运算，并在添加标量偏置之后产生输出。所以，卷积层中的两个被训练的参数是卷积核权重核标量偏置。就像我们之前随机初始化全连接层一样，在训练基于卷积层的模型时，我们也随机初始化卷积核权重。

基于上面定义的corr2d函数实现二维卷积层。在__init__构造函数中，将weight和bias声明为两个模型参数。前向传播函数调用corr2d函数并添加偏置。

class Conv2D(nn.Module):
	def __init__(self, kernel_size):
		super().__init__()
		self.weight = nn.Parameter(torch.rand(kernel_size))
		self.bias = nn.Parameter(torch.zeros(1))

	def forward(self, x):
		return corr2d(x, self.weight) + self.bias

高度和宽度分别为 h和 w的卷积核可以被称为 h × w 卷积或 h × w 卷积核。我们也将带有 h × w 卷积核的卷积层称为 h × w 卷积层。

特征映射

下图中输出的卷积层有时被称为特征映射（Feature Map），因为它可以被视为一个输入映射到下一层的空间维度的转换器。在CNN中，对于某一层的任意元素 x x x，其感受野（Receptive Field）是指在前向传播期间可能影响 x x x计算的所有元素（来自所有先前层）。

注意，感受野的覆盖率可能大于某层输入的实际区域大小。

例如上图：给定 2 × 2 卷积核，阴影输出元素值19的接收域是阴影部分的四个元素。假设之前输出为 Y ，其大小为 2 × 2 ，现在我们再其后附加一个卷积层，该卷积层以 Y 为输入，输出单个元素 z。再这种情况下， Y上的  z的接收字段包括 Y 的所有四个元素，而输入的感受野包括最初所有九个输入元素。
因此，当一个特征图中的任意元素需要检测更广区域的输入特征时，我们可以构建一个更深的网络。

以上就是Python深度学习pytorch神经网络图像卷积运算详解的详细内容，更多关于pytorch神经网络图像卷积运算的资料请关注我们其它相关文章！

赞 (0)

相关推荐

  • PyTorch上实现卷积神经网络CNN的方法

    一.卷积神经网络 卷积神经网络(ConvolutionalNeuralNetwork,CNN)最初是为解决图像识别等问题设计的,CNN现在的应用已经不限于图像和视频,也可用于时间序列信号,比如音频信号和文本数据等.CNN作为一个深度学习架构被提出的最初诉求是降低对图像数据预处理的要求,避免复杂的特征工程.在卷积神经网络中,第一个卷积层会直接接受图像像素级的输入,每一层卷积(滤波器)都会提取数据中最有效的特征,这种方法可以提取到图像中最基础的特征,而后再进行组合和抽象形成更高阶的特征,因此CNN在

  • pytorch中的卷积和池化计算方式详解

    TensorFlow里面的padding只有两个选项也就是valid和same pytorch里面的padding么有这两个选项,它是数字0,1,2,3等等,默认是0 所以输出的h和w的计算方式也是稍微有一点点不同的:tf中的输出大小是和原来的大小成倍数关系,不能任意的输出大小:而nn输出大小可以通过padding进行改变 nn里面的卷积操作或者是池化操作的H和W部分都是一样的计算公式:H和W的计算 class torch.nn.MaxPool2d(kernel_size, stride=Non

  • pytorch神经网络之卷积层与全连接层参数的设置方法

    当使用pytorch写网络结构的时候,本人发现在卷积层与第一个全连接层的全连接层的input_features不知道该写多少?一开始本人的做法是对着pytorch官网的公式推,但是总是算错. 后来发现,写完卷积层后可以根据模拟神经网络的前向传播得出这个. 全连接层的input_features是多少.首先来看一下这个简单的网络.这个卷积的Sequential本人就不再啰嗦了,现在看nn.Linear(???, 4096)这个全连接层的第一个参数该为多少呢? 请看下文详解. class AlexN

  • Pytorch中膨胀卷积的用法详解

    卷积和膨胀卷积 在深度学习中,我们会碰到卷积的概念,我们知道卷积简单来理解就是累乘和累加,普通的卷积我们在此不做赘述,大家可以翻看相关书籍很好的理解. 最近在做项目过程中,碰到Pytorch中使用膨胀卷积的情况,想要的输入输出是图像经过四层膨胀卷积后图像的宽高尺寸不发生变化. 开始我的思路是padding='SAME'结合strides=1来实现输入输出尺寸不变,试列好多次还是有问题,报了张量错误的提示,想了好久也没找到解决方法,上网搜了下,有些人的博客说经过膨胀卷积之后图像的尺寸不发生变化,有

  • Pytorch之卷积层的使用详解

    1.简介(torch.nn下的) 卷积层主要使用的有3类,用于处理不同维度的数据 参数 Parameters: in_channels(int) – 输入信号的通道 out_channels(int) – 卷积产生的通道 kerner_size(int or tuple) - 卷积核的尺寸 stride(int or tuple, optional) - 卷积步长 padding (int or tuple, optional)- 输入的每一条边补充0的层数 dilation(int or tu

  • Python深度学习pytorch神经网络图像卷积运算详解

    Python深度学习pytorch神经网络图像卷积运算详解

    目录 互相关运算 卷积层 特征映射 由于卷积神经网络的设计是用于探索图像数据,本节我们将以图像为例. 互相关运算 严格来说,卷积层是个错误的叫法,因为它所表达的运算其实是互相关运算(cross-correlation),而不是卷积运算.在卷积层中,输入张量和核张量通过互相关运算产生输出张量. 首先,我们暂时忽略通道(第三维)这一情况,看看如何处理二维图像数据和隐藏表示.下图中,输入是高度为3.宽度为3的二维张量(即形状为 3 × 3 3\times3 3×3).卷积核的高度和宽度都是2. 注意,

  • Python深度学习pytorch神经网络填充和步幅的理解

    Python深度学习pytorch神经网络填充和步幅的理解

    目录 填充 步幅 上图中,输入的高度和宽度都为3,卷积核的高度和宽度都为2,生成的输出表征的维度为 2 × 2 2\times2 2×2.从上图可看出卷积的输出形状取决于输入形状和卷积核的形状. 填充 以上面的图为例,在应用多层卷积时,我们常常丢失边缘像素. 解决这个问题的简单方法即为填充(padding):在输入图像的边界填充元素(通常填充元素是0). 例如,在上图中我们将 3 × 3 3\times3 3×3输入填充到 5 × 5 5\times5 5×5,那么它的输出就增加为 4 × 4

  • Python深度学习pytorch神经网络汇聚层理解

    Python深度学习pytorch神经网络汇聚层理解

    目录 最大汇聚层和平均汇聚层 填充和步幅 多个通道 我们的机器学习任务通常会跟全局图像的问题有关(例如,"图像是否包含一只猫呢?"),所以我们最后一层的神经元应该对整个输入的全局敏感.通过逐渐聚合信息,生成越来越粗糙的映射,最终实现学习全局表示的目标,同时将卷积图层的所有有时保留在中间层. 此外,当检测较底层的特征时(例如之前讨论的边缘),我们通常希望这些特征保持某种程度上的平移不变性.例如,如果我们拍摄黑白之间轮廓清晰的图像X,并将整个图像向右移动一个像素,即Z[i, j] = X[

  • Python深度学习pytorch神经网络多输入多输出通道

    Python深度学习pytorch神经网络多输入多输出通道

    目录 多输入通道 多输出通道 1 × 1 1\times1 1×1卷积层 虽然每个图像具有多个通道和多层卷积层.例如彩色图像具有标准的RGB通道来指示红.绿和蓝.但是到目前为止,我们仅展示了单个输入和单个输出通道的简化例子.这使得我们可以将输入.卷积核和输出看作二维张量. 当我们添加通道时,我们的输入和隐藏的表示都变成了三维张量.例如,每个RGB输入图像具有 3 × h × w 3\times{h}\times{w} 3×h×w的形状.我们将这个大小为3的轴称为通道(channel)维度.在本节

  • Python深度学习pytorch神经网络Dropout应用详解解

    Python深度学习pytorch神经网络Dropout应用详解解

    目录 扰动的鲁棒性 实践中的dropout 简洁实现 扰动的鲁棒性 在之前我们讨论权重衰减(L2​正则化)时看到的那样,参数的范数也代表了一种有用的简单性度量.简单性的另一个有用角度是平滑性,即函数不应该对其输入的微笑变化敏感.例如,当我们对图像进行分类时,我们预计向像素添加一些随机噪声应该是基本无影响的. dropout在正向传播过程中,计算每一内部层同时注入噪声,这已经成为训练神经网络的标准技术.这种方法之所以被称为dropout,因为我们从表面上看是在训练过程中丢弃(drop out)一些

  • Python深度学习pytorch神经网络多层感知机简洁实现

    Python深度学习pytorch神经网络多层感知机简洁实现

    我们可以通过高级API更简洁地实现多层感知机. import torch from torch import nn from d2l import torch as d2l 模型 与softmax回归的简洁实现相比,唯一的区别是我们添加了2个全连接层.第一层是隐藏层,它包含256个隐藏单元,并使用了ReLU激活函数.第二层是输出层. net = nn.Sequential(nn.Flatten(), nn.Linear(784, 256), nn.ReLU(), nn.Linear(256, 1

  • Python深度学习pytorch神经网络块的网络之VGG

    Python深度学习pytorch神经网络块的网络之VGG

    目录 VGG块 VGG网络 训练模型 与芯片设计中工程师从放置晶体管到逻辑元件再到逻辑块的过程类似,神经网络结构的设计也逐渐变得更加抽象.研究人员开始从单个神经元的角度思考问题,发展到整个层次,现在又转向模块,重复各层的模式. 使用块的想法首先出现在牛津大学的视觉几何组(visualgeometry Group)(VGG)的VGG网络中.通过使用循环和子程序,可以很容易地在任何现代深度学习框架的代码中实现这些重复的结构. VGG块 经典卷积神经网络的基本组成部分是下面的这个序列: 1.带填充以保

  • Python深度学习pytorch卷积神经网络LeNet

    Python深度学习pytorch卷积神经网络LeNet

    目录 LeNet 模型训练 在本节中,我们将介绍LeNet,它是最早发布的卷积神经网络之一.这个模型是由AT&T贝尔实验室的研究院Yann LeCun在1989年提出的(并以其命名),目的是识别手写数字.当时,LeNet取得了与支持向量机性能相媲美的成果,成为监督学习的主流方法.LeNet被广泛用于自动取款机中,帮助识别处理支票的数字. LeNet 总体来看,LeNet(LeNet-5)由两个部分组成: 卷积编码器: 由两个卷积层组成 全连接层密集快: 由三个全连接层组成 每个卷积块中的基本单元

  • Python深度学习pytorch实现图像分类数据集

    Python深度学习pytorch实现图像分类数据集

    目录 读取数据集 读取小批量 整合所有组件 目前广泛使用的图像分类数据集之一是MNIST数据集.如今,MNIST数据集更像是一个健全的检查,而不是一个基准. 为了提高难度,我们将在接下来的章节中讨论在2017年发布的性质相似但相对复杂的Fashion-MNIST数据集. import torch import torchvision from torch.utils import data from torchvision import transforms from d2l import to

  • Python scipy的二维图像卷积运算与图像模糊处理操作示例

    本文实例讲述了Python scipy的二维图像卷积运算与图像模糊处理操作.分享给大家供大家参考,具体如下: 二维图像卷积运算 一 代码 import numpy as np from scipy import signal, misc import matplotlib.pyplot as plt image = misc.ascent()#二维图像数组,lena图像 w = np.zeros((50,50))#全0二维数组,卷积核 w[0][0]=1.0#修改参数,调整滤波器 w[49][2

随机推荐