图解Java中归并排序算法的原理与实现

目录

• 一、基本思想
• 二、算法分析
• 1、算法描述
• 2、过程分析
• 3、动图演示
• 三、算法实现

一、基本思想

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

二、算法分析

1、算法描述

把长度为n的输入序列分成两个长度为n/2的子序列；对这两个子序列分别采用归并排序；将两个排序好的子序列合并成一个最终的排序序列。

2、过程分析

（1）、现在我们将拆分项 [1] (指数从 0 到 0，两边都包括) 和 [28] 指数从 1 到 1 ，两边都包括) 归并在一起。

（2）、因为 1 (左拆分) <= 28 (右拆分), 我们将 {rightPart} 拷进新的数组。

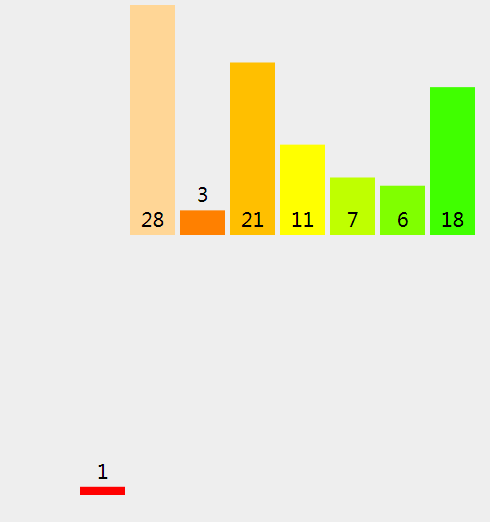
（3）、因为左拆分是空的，我们将 28 （右拆分）拷进新的数组。

（4）、我们将新数组中的元素拷贝回原来的数组中。

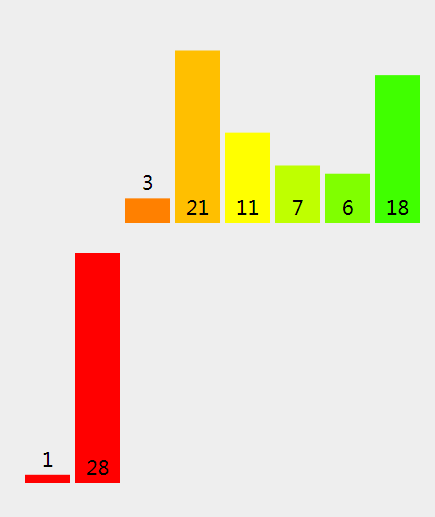
（5）、因为 3 (左拆分) <= 21 (右拆分), 我们将 {rightPart} 拷进新的数组。

（6）、因为左拆分是空的，我们将 21 （右拆分）拷进新的数组。

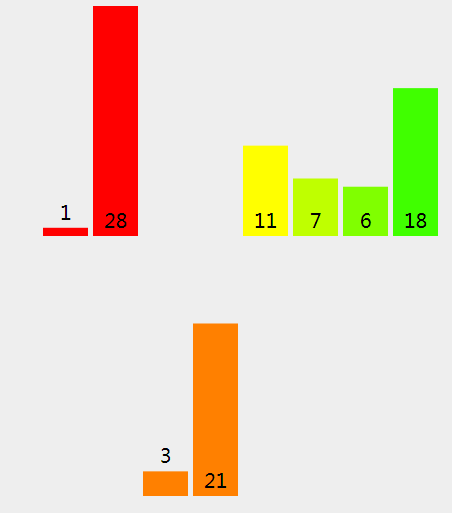
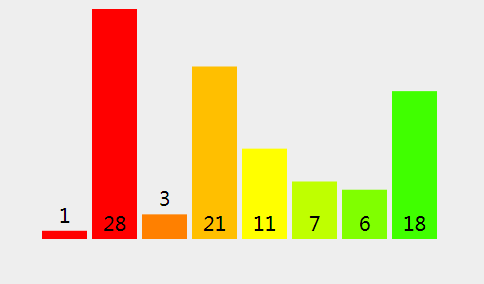
（7）、现在我们将拆分项 [1,28] (指数从 0 到 1，两边都包括) 和 [3,21] 指数从 2 到 3 ，两边都包括) 归并在一起。

（8）、因为 1 (左拆分) <= 3 (右拆分), 我们将 {rightPart} 拷进新的数组。

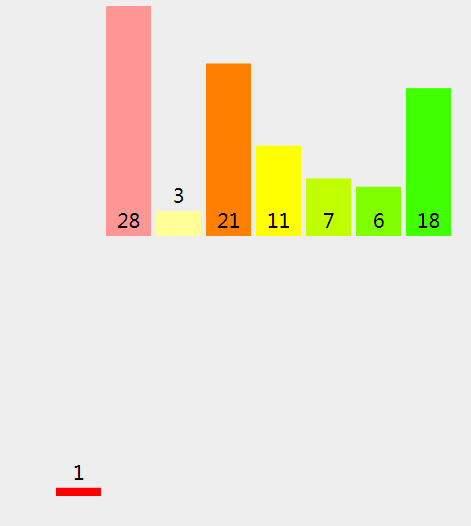
（9）、因为 28 (左拆分) > 3 (右拆分), 我们将 {rightPart} 拷进新的数组。

（10）、因为 28 (左拆分) > 21 (右拆分), 我们将 {rightPart} 拷进新的数组。

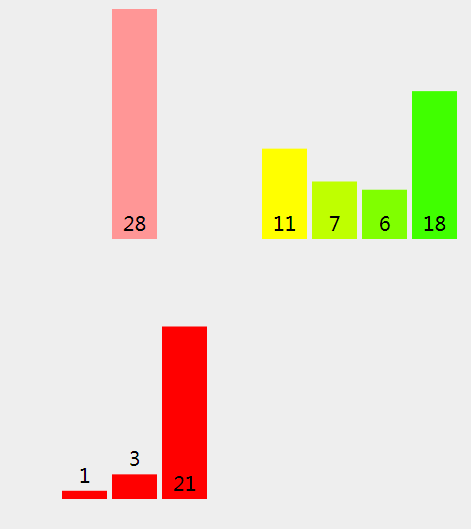
（11）、因为右拆分是空的，我们将28 (左拆分) 拷贝进新的数组。

（12）、我们将新数组中的元素拷贝回原来的数组中。

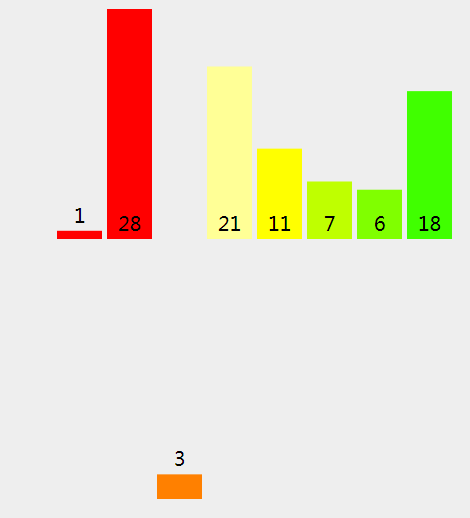
（13）、现在我们将拆分项 [11] (指数从 4 到 4，两边都包括) 和 [7] 指数从 5 到 5 ，两边都包括) 归并在一起。

（14）、因为 11 (左拆分) > 7 (右拆分), 我们将 {rightPart} 拷进新的数组。

（15）、因为右拆分是空的，我们将11 (左拆分) 拷贝进新的数组。

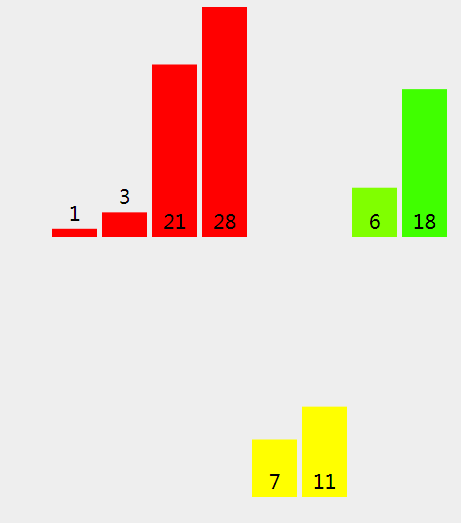
（16）、我们将新数组中的元素拷贝回原来的数组中。

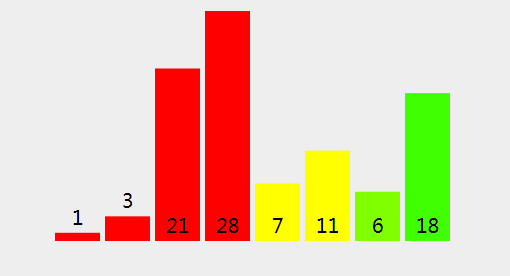
（17）、以此类推

（18）、因为 1 (左拆分) <= 6 (右拆分), 我们将 {rightPart} 拷进新的数组。

（19）、因为 3 (左拆分) <= 6 (右拆分), 我们将 {rightPart} 拷进新的数组。

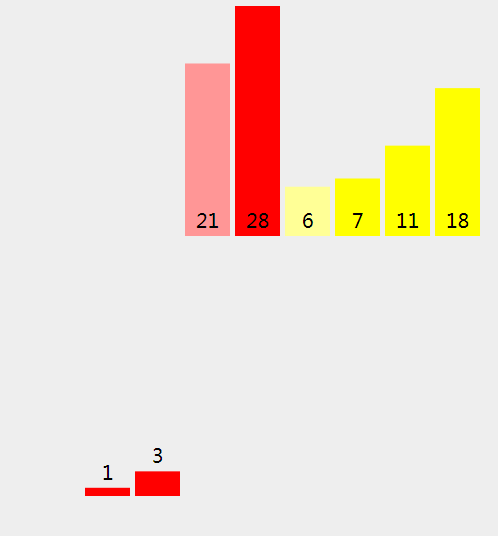
（20）、因为 21 (左拆分) > 6 (右拆分), 我们将 {rightPart} 拷进新的数组。

（21）、因为 21 (左拆分) > 7 (右拆分), 我们将 {rightPart} 拷进新的数组。

（22）、以此类推，我们将新数组中的元素拷贝回原来的数组中。

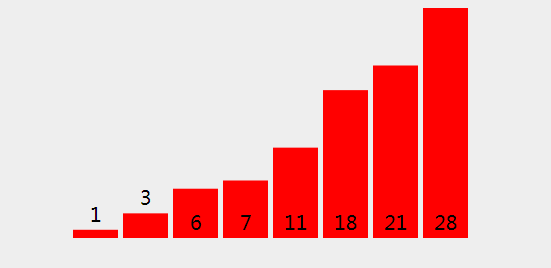
3、动图演示

三、算法实现

package com.algorithm.tenSortingAlgorithm;

import java.util.Arrays;

public class MergeSort {
    private static void mergeSort(int[] arr, int low, int high) {
        if (low < high) { //当子序列中只有一个元素时结束递归
            int mid = (low + high) / 2; //划分子序列
            mergeSort(arr, low, mid); //对左侧子序列进行递归排序
            mergeSort(arr, mid + 1, high); //对右侧子序列进行递归排序
            merge(arr, low, mid, high); //合并
        }
    }

    private static void merge(int[] arr, int low, int mid, int high) {
        int[] temp = new int[arr.length]; //辅助数组
        int k = 0, i = low, j = mid + 1; //i左边序列和j右边序列起始索引,k是存放指针
        while (i <= mid && j <= high) {
            if (arr[i] <= arr[j]) {
                temp[k++] = arr[i++];
            } else {
                temp[k++] = arr[j++];
            }
        }
        //如果第一个序列未检测完，直接将后面所有元素加到合并的序列中
        while (i <= mid) {
            temp[k++] = arr[i++];
        }
        //同上
        while (j <= high) {
            temp[k++] = arr[j++];
        }
        //复制回原数组
        for (int t = 0; t < k; t++) {
            arr[low + t] = temp[t];
        }
    }

    public static void main(String[] args) {
        int[] arr = {1,28,3,21,11,7,6,18};
        mergeSort(arr, 0, arr.length - 1);
        System.out.println(Arrays.toString(arr));
    }
}

到此这篇关于图解Java中归并排序算法的原理与实现的文章就介绍到这了,更多相关Java归并排序内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！