二叉查找树的插入,删除,查找

二叉查找树是满足以下条件的二叉树：
1、左子树上的所有节点值均小于根节点值，
2、右子树上的所有节点值均不小于根节点值，
3、左右子树也满足上述两个条件。

二叉查找树的插入过程如下：
1.若当前的二叉查找树为空，则插入的元素为根节点，
2.若插入的元素值小于根节点值，则将元素插入到左子树中，
3.若插入的元素值不小于根节点值，则将元素插入到右子树中。

二叉查找树的删除，分三种情况进行处理：
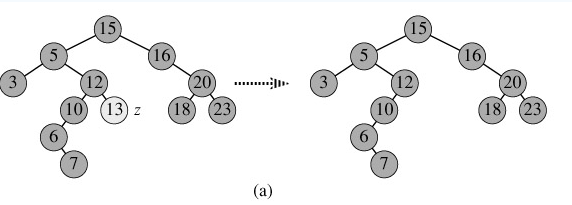
1.p为叶子节点，直接删除该节点，再修改其父节点的指针（注意分是根节点和不是根节点），如图a。

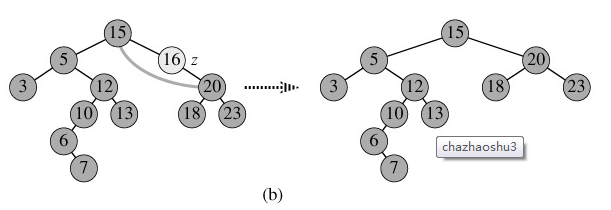
2.p为单支节点（即只有左子树或右子树）。让p的子树与p的父亲节点相连，删除p即可；（注意分是根节点和不是根节点）；如图b。

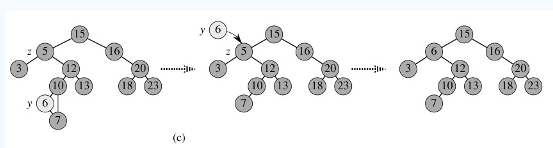
3.p的左子树和右子树均不空。找到p的后继y，因为y一定没有左子树，所以可以删除y，并让y的父亲节点成为y的右子树的父亲节点，并用y的值代替p的值；或者方法二是找到p的前驱x，x一定没有右子树，所以可以删除x，并让x的父亲节点成为y的左子树的父亲节点。如图c。

插入节点的代码：


代码如下:

struct node
{
    int val;
    pnode lchild;
    pnode rchild;
};

pnode BT = NULL;

//递归方法插入节点
pnode insert(pnode root, int x)
{
    pnode p = (pnode)malloc(LEN);
    p->val = x;
    p->lchild = NULL;
    p->rchild = NULL;
    if(root == NULL){
        root = p;   
    }   
    else if(x < root->val){
        root->lchild = insert(root->lchild, x);   
    }
    else{
        root->rchild = insert(root->rchild, x);   
    }
    return root;
}

//非递归方法插入节点
void insert_BST(pnode q, int x)
{
    pnode p = (pnode)malloc(LEN);
    p->val = x;
    p->lchild = NULL;
    p->rchild = NULL;
    if(q == NULL){
        BT = p;
        return ;   
    }       
    while(q->lchild != p && q->rchild != p){
        if(x < q->val){
            if(q->lchild){
                q = q->lchild;   
            }   
            else{
                q->lchild = p;
            }       
        }   
        else{
            if(q->rchild){
                q = q->rchild;   
            }   
            else{
                q->rchild = p;   
            }
        }
    }
    return;
}

查找节点的代码：


代码如下:

pnode search_BST(pnode p, int x)
{
    bool solve = false;
    while(p && !solve){
        if(x == p->val){
            solve = true;   
        }   
        else if(x < p->val){
            p = p->lchild;   
        }
        else{
            p = p->rchild;   
        }
    }
    if(p == NULL){
        cout << "没有找到" << x << endl;   
    }
    return p;
}

删除节点的代码


代码如下:

bool delete_BST(pnode p, int x) //返回一个标志，表示是否找到被删元素
{
    bool find = false;
    pnode q;
    p = BT;
    while(p && !find){  //寻找被删元素
        if(x == p->val){  //找到被删元素
            find = true;   
        }   
        else if(x < p->val){ //沿左子树找
            q = p;
            p = p->lchild;   
        }
        else{   //沿右子树找
            q = p;
            p = p->rchild;   
        }
    }
    if(p == NULL){   //没找到
        cout << "没有找到" << x << endl;   
    }

if(p->lchild == NULL && p->rchild == NULL){  //p为叶子节点
        if(p == BT){  //p为根节点
            BT = NULL;   
        }
        else if(q->lchild == p){  
            q->lchild = NULL;
        }       
        else{
            q->rchild = NULL;   
        }
        free(p);  //释放节点p
    }
    else if(p->lchild == NULL || p->rchild == NULL){ //p为单支子树
        if(p == BT){  //p为根节点
            if(p->lchild == NULL){
                BT = p->rchild;   
            }   
            else{
                BT = p->lchild;   
            }
        }   
        else{
            if(q->lchild == p && p->lchild){ //p是q的左子树且p有左子树
                q->lchild = p->lchild;    //将p的左子树链接到q的左指针上
            }   
            else if(q->lchild == p && p->rchild){
                q->lchild = p->rchild;   
            }
            else if(q->rchild == p && p->lchild){
                q->rchild = p->lchild;   
            }
            else{
                q->rchild = p->rchild;
            }
        }
        free(p);
    }
    else{ //p的左右子树均不为空
        pnode t = p;
        pnode s = p->lchild;  //从p的左子节点开始
        while(s->rchild){  //找到p的前驱，即p左子树中值最大的节点
            t = s;  
            s = s->rchild;   
        }
        p->val = s->val;   //把节点s的值赋给p
        if(t == p){
            p->lchild = s->lchild;   
        }   
        else{
            t->rchild = s->lchild;   
        }
        free(s);
    }
    return find;
}