Android实现左右摆动的球体动画效果

首先，看一下效果

可能各位在别处看到过类似的东西，我在微信的文章末尾看到有个玩意，感觉有意思，就用代码实现一下。这篇文章主要把握写代码的思路展示一下。

看到上图，我想各位能想到最简单的实现方案就是用动画，切很多图出来，然后就可以轻松实现了。为了不让自己再舒适区里呆的太安逸，就弄点麻烦的：通过计算来实现。文章的末尾会将全部代码贴出，复制可以直接运行。

需要回忆的知识

重力势能 E = mgh

动能 E = ½mv²

在理想状态下，动能和重力式能可以相互转换，且能量守恒

如果不想太注意细节，以上的知识可以忽略

绘制流程

绘制5个带绳子的球

这步非常简单，概括来说就是：

确定球的圆心坐标O

画固定长度的线段OA

以点O为圆心，画固定半径的球（这样就完成了一个带绳的球）

绘制多个带绳的球

相关代码在文章末尾已经贴出来了（78-121行，代码中有后续的细节处理，需要甄别下相关的代码），这里只是写下思路，不再重复

贴代码了

让球旋转

静态图为：

让带绳子的球旋转，实际上就是改变上图的角α；当α越大，偏移的角度越大；当α越小，偏移的角度越小。
为了让计算简单，先假设一些前提：

1.α的最大值为45°（这里可以自由给值）

2.每次刷新屏幕α改变的值的大小一致且为1（也就是调用invalidate()方法）

3.一开始α为45°

有了这些前提限制，实际上，每一次绘图我们的已知条件为：

1.O点的坐标

2.大圆的半径 = 绳子的长度 + 小圆的半径

3.α的值（因为前提中的2和3，绘制的时候是可以知道当前α的角度）

所以，这步的大致流程为：

1.根据大圆的圆心O、半径R，当前α的角度，求B点的坐标（跟前一篇类似，通过画弧，再通过PathMeasure.getPosTan()来获得相应点的坐标）

2.绘制线段OB

3.以B点为圆心，画半径为固定值的小圆

相关代码在文章末尾已经贴出来了（128-212行，代码中有后续的细节处理，需要甄别下相关的代码），这里只是写下思路，不再重

复贴代码了

模拟现实

在上一步中，我们为了简化模型，让α的改变量每次都为1，但是，这与现实不相符。现实情况是这样的：

1.球偏移到最高点时，速度很慢，基本上为0

2.球偏移到最低点，速度最快

文章一开始，我们已经准备好了需要回忆的知识，现在，让我们回到物理学课堂，说一说简单的摆钟模型计算：

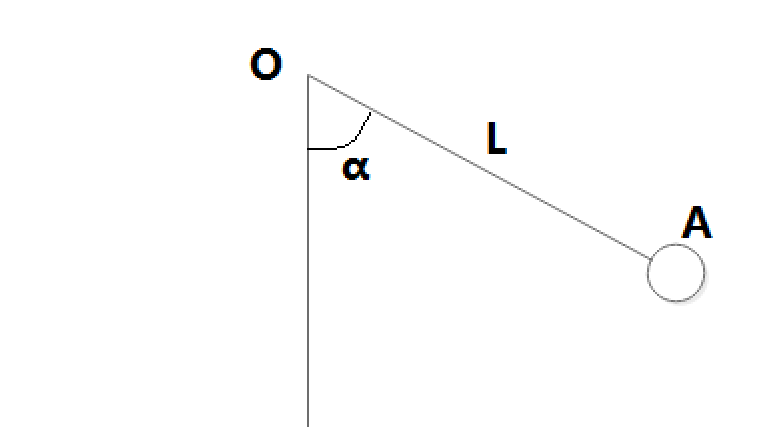
条件：绳子的长为L，球A静止时，竖直方向的夹角为α

求：当与竖直方向的夹角为β时的角速度

解题步骤求总机械能

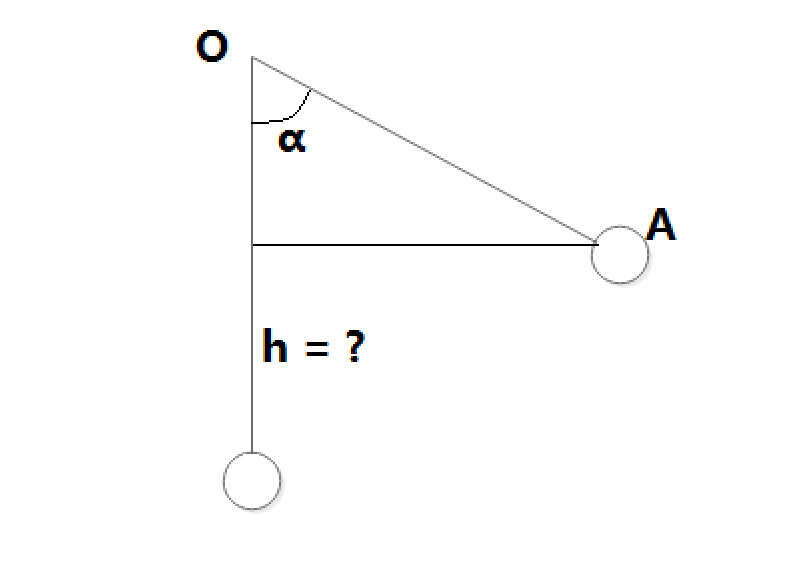
当球静止时，机械能 = 重力势能

一般情况的表示

当球运动时，机械能 = 重力势能 + 动能

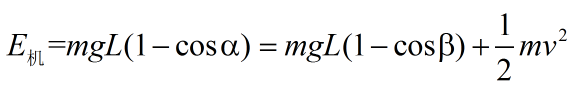
又有公式：

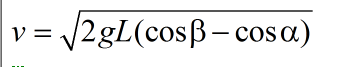
所以最终结果为：

好了，得出了结论，让我们回到代码中来：

//计算当前的速率
float v = (float) Math.sqrt(2 * 9.8 * L * (Math.cos( β* Math.PI / 180) - cos(α* Math.PI / 180)));
//计算角速度
float w = v / L;

说明：这里只是拟合，并没有特别精确。我们认为当前角度到改变后的角度之间的角速度是一致的，都为当前角度所对应的角速度；

所以，在当前角度下，改变角度的量为：

具体的实现过程在下面代码的219-225行，是不是感觉很简单？

全部代码

上面罗里吧嗦的半天，终于给出来了可以复制的东西 O(∩_∩)O~

/**
* Created by kevin on 2016/9/2.
* <p>
* 需要推敲的地方：
* 1.并排绘制多个带绳子的球
* 2.让左右两端的球可以旋转
* 3.为了模拟现实，需要根据物理学来计算单位时间旋转的角度
*/
public class Pendulum extends View {
private Paint linePaint;
private int width;
private int height;
private Path linePath;//用来绘制静态部分的Path
private Path bigCirclePath;//用来测量大圆的Path
private Path rotateLinePath;//用来绘制动态部分的Path
private int stroke = 5; //线段的宽度
private int r = 20; //圆圈的半径
private int length = 200; //线的长度
private int number = 5; //球的个数（奇数，偶数感觉丑就没实现）
private static int angle = 50;//最大旋转角度
// 第一个参数表示角度；负数表示左边球旋转的角度，正数表示右边球旋转的角度
// +angle表示右侧球偏离最大的角度为30度
// -angle表示左侧球偏离最大的角度为30度
// 第二个参数表示方向；-1表示从右往左摆动，1表示从左往右摆动
private float[] degree = new float[]{angle, -1};
private float t = 2f;//时间；可以用来控制速率，t越小，摆钟越慢；t越大，摆钟越快
private float cosO;//cosθ,是个固定值
private float gr2;//2gr，是个固定值
public Pendulum(Context context) {
super(context);
initPaint();
calCosOAnd2gr();
}
public Pendulum(Context context, AttributeSet attrs) {
super(context, attrs);
initPaint();
calCosOAnd2gr();
}
public Pendulum(Context context, AttributeSet attrs, int defStyleAttr) {
super(context, attrs, defStyleAttr);
initPaint();
calCosOAnd2gr();
}
/**
* 用来计算cosθ和2gr
*/
private void calCosOAnd2gr() {
//这里为了避免cosα-cosθ=0的情况，所以+0.1
cosO = (float) Math.cos((angle + 0.1f) * Math.PI / 180);
//2倍的重力加速度乘以半径
gr2 = (float) (9.8 * r * 2);
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
canvas.translate(width / 2, height / 2);
drawPic(canvas);
rotate(canvas);
}
/**
* 绘制静态图形
*
* @param canvas
*/
private void drawPic(Canvas canvas) {
if (number < 1) {
throw new IllegalArgumentException("数量不能小于1");
}
int x;
if (number % 2 == 1) {
//奇数的情况
//用来确定最外层的位置，例如：如果number为3，leftNumber为1
// number为5，leftNumber为2
// number为7，leftNumber为3
int leftNumber = number / 2;
for (int i = -leftNumber; i <= leftNumber; i++) {
if (isRight()) {
//最右侧在摇摆
if (i == leftNumber)
continue;
} else if (!isRight()) {
//最左侧的在摇摆
if (i == -leftNumber)
continue;
}
//计算圆心的横坐标x
x = 2 * r * i;
if (linePath == null)
linePath = new Path();
linePath.reset();
//move到圆心(更准确的坐标为(x,-r),圆绘制出来会把部分线段覆盖；这里只是为了方便表示，不再增加多余的点)
linePath.moveTo(x, 0);
//画直线到顶点，（顶点离圆心= 线段的长度 + 半径）
linePath.lineTo(x, -(r + length));
//绘制直线
linePaint.setStyle(Paint.Style.FILL_AND_STROKE);
canvas.drawPath(linePath, linePaint);
//绘制圆圈，为了不重合，使用FILL，不绘制线的宽度
linePaint.setStyle(Paint.Style.FILL);
canvas.drawCircle(x, 0, r, linePaint);
}
} else if (number % 2 == 0) {
//偶数
throw new IllegalArgumentException("偶数太丑，没有绘制");
}
}
/**
* 绘制旋转的图形
*
* @param canvas
*/
private void rotate(Canvas canvas) {
//左侧球运动和右侧球运动是对称的，使用direction（值为+1或-1）来做标记
int direction;
if (isRight()) {
//右侧球运动，+1
direction = 1;
} else {
//左侧球于东，-1
direction = -1;
}
//measure.getPosTan()中不接受负数，这里需要取绝对值
float nowDegree = Math.abs(degree[0]);
linePaint.setStyle(Paint.Style.STROKE);
//确定单侧外层图片的个数
int pointNumber = number / 2;
//确定静态圆形的横坐标，与drawPic中的（x = 2 * r * i）相似
int x = 2 * r * pointNumber * direction;
//用来确定大圆圆心的坐标，同时也是线段顶点的坐标
float[] topPoint = new float[]{x, -(r + length)};
int totalLength = length + r;
if (bigCirclePath == null)
bigCirclePath = new Path();
bigCirclePath.reset();
//rectF是用来绘制弧形的：以线段的顶点为圆心，length + r为半径画弧形
RectF rectF = new RectF(topPoint[0] - totalLength, topPoint[1] - totalLength, topPoint[0] + totalLength, topPoint[1] + totalLength);
//绘制1/4个圆的弧形
bigCirclePath.addArc(rectF, 90, -90 * direction);
//用来确定旋转nowDegree时的边界坐标；
float[] rotatePoint = new float[2];
PathMeasure measure = new PathMeasure(bigCirclePath, false);
//此时，rotatePoint的坐标就为我们图中小圆圈圆心的坐标
measure.getPosTan(measure.getLength() * (nowDegree) / 90, rotatePoint, null);
//到现在为止，我们已经知道了圆心的坐标以及线段顶点的坐标了。
//下面，我们就链接这个两个点，并以rotatePoint为圆心画圆
//画线段
if (rotateLinePath == null)
rotateLinePath = new Path();
rotateLinePath.reset();
rotateLinePath.moveTo(topPoint[0], topPoint[1]);
rotateLinePath.lineTo(rotatePoint[0], rotatePoint[1]);
canvas.drawPath(rotateLinePath, linePaint);
//画圆
linePaint.setStyle(Paint.Style.FILL);
canvas.drawCircle(rotatePoint[0], rotatePoint[1], r, linePaint);
//显示文字用的，不用理会
linePaint.setTextSize(40);
canvas.drawText("偏移的角度：" + degree[0] + "", -100, 100, linePaint);
//degree[1]表示方向，当为1时，表示从左向右运动，那么degree[0]需要不断增加（这是我规定的；当然要修改的话，可以根据情况来修改，估计修改时会晕菜一段时间）
if (degree[1] == 1) {
//从总往右,degree增大
if (degree[0] < angle) {
//计算需要转动的角度
float changeAngle = rotateAngle();
//改变当前角度的值
degree[0] = degree[0] + changeAngle;
invalidate();
}
//当达到最右侧时，方向翻转
if (degree[0] >= angle) {
degree[1] = -1;
}
}
//degree[1]表示方向，当为-1时，表示从右向左运动，那么degree[0]需要不断减小（这是我规定的；当然要修改的话，可以根据情况来修改，估计修改时会晕菜一段时间）
else if (degree[1] == -1) {
//从右往左，degree减小
if (degree[0] > -angle) {
//计算需要转动的角度
float changeAngle = rotateAngle();
//改变当前角度的值
degree[0] = degree[0] - changeAngle;
invalidate();
}
//当达到最左侧时，方向翻转
if (degree[0] <= -angle) {
degree[1] = 1;
}
}
}
/**
* 计算当前需要转动的角度
*
* @return
*/
private float rotateAngle() {
//计算当前的速率
float v = (float) Math.sqrt(gr2 * (Math.cos(Math.abs(degree[0]) * Math.PI / 180) - cosO));
//计算需要改变的弧度
float changedAngle = t * v / r;
return changedAngle;
}
/**
* 判断是否是右侧的圆球在动
*
* @return true-->右侧的圆球在动
* false-->左侧的圆球在动
*/
private boolean isRight() {
boolean flag = false;
//degree[0]大于0，表示右侧球在动
//degree[1]小于0，表示左侧球在动
if (degree[0] > 0) {
flag = true;
} else if (degree[0] < 0) {
flag = false;
} else if (degree[0] == 0) {
//如果degree等于0，需要根据方向来判断哪个求在动
//degree[1]等于-1表示：球是从右往左在运动，此时，球的速度 v-->0，但还是右侧的球在动
if (degree[1] == -1) {
flag = true;
}
//与上面的情况相反，是左侧的球在动
else if (degree[1] == 1) {
flag = false;
}
}
return flag;
}
@Override
protected void onSizeChanged(int w, int h, int oldw, int oldh) {
super.onSizeChanged(w, h, oldw, oldh);
width = w;
height = h;
}
private void initPaint() {
//这里不想弄多个Paint,就用一个Paint来替代了，如果有需要，可以增加Paint来绘制指定的图形
linePaint = new Paint();
linePaint.setStrokeWidth(stroke);
linePaint.setAntiAlias(true);
linePaint.setStyle(Paint.Style.FILL_AND_STROKE);
linePaint.setColor(0xff4897fe);
}
}

以上所述是小编给大家介绍的Android实现左右摆动的球体动画效果，希望对大家有所帮助，如果大家有任何疑问请给我留言，小编会及时回复大家的。在此也非常感谢大家对我们网站的支持！