opengl实现直线扫描算法和区域填充算法

本文实例为大家分享了opengl实现直线扫描算法和区域填充算法，供大家参考，具体内容如下

总体介绍

1、采用直线扫描算法绘制一条线段，直线由离散点组成

2、利用区域填充算法绘制多边形区域，区域由离散点组成

开发环境VS2012+OpenGL

开发平台 Intel core i5,Intel HD Graphics Family

设计思路

一、直线扫描算法

1、数值微分法（DDA）

已知过端点P0 (x0, y0), P1(x1, y1)的直线段L：y = kx + b，容易得知直线斜率为：k = (y1-y0)/(x1-x0)，（假设x1≠x0）。

我们假设|k|≤1，这样x每增加1，y将增加k，并且保证x每增加1，y的增量不能大于1；如果|k| > 1,则应该将x和y互换。由于k是浮点数，因此算法中需要将y舍入为int型，并圆整到最接近的位置。

DDA算法在每次迭代中的x, y值是上一步的值加上一个增量获得的，因此它是一个增量算法。但是这种方法直观，但效率太低，因为每一步需要一次浮点乘法和一次舍入运算。

2、中点画线法

在直线斜率在0~1直接的情况下，设当前像素点为(x,y)，那么它的下一个像素点就是p1(x+1,y)或者p2(x+1,y+1)，若称p1和p2的中点M(px+1,y+0.5)，Q为理想直线与x+1垂线的交点，当Q在M的下方时，p1即为下一个像素点，否则p2即为下一个像素点。

3、Bresenham算法

过各行各列象素中心构造一组虚拟网格线。按直线从起点到终点的顺序计算直线与各垂直网格线的交点，然后确定该列象素中与此交点最近的象素。该算法的巧妙之处在于采用增量计算，使得对于每一列，只要检查一个误差项的符号，就可以确定该列的所求象素。

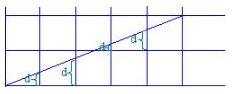
如图所示，设直线方程为yi+1=yi+k(xi+1-xi)+k。假设列坐标象素已经确定为xi，其行坐标为yi。那么下一个象素的列坐标为xi＋1，而行坐标要么为yi，要么递增1为yi＋1。是否增1取决于误差项d的值。误差项d的初值d0＝0，x坐标每增加1，d的值相应递增直线的斜率值k，即d＝d＋k。一旦  d≥1，就把它减去1，这样保证d在0、1之间。当d≥0.5时，直线与垂线x=xi＋1交点最接近于当前象素(xi，yi)的右上方象素(xi＋1，yi＋1)；而当d<0.5时，更接近于右方象素(xi＋1，yi)。为方便计算，令e＝d－0.5，e的初值为－0.5，增量为k。当e≥0时，取当前象素(xi，yi)的右上方象素(xi＋1，yi＋1)；而当e<0时，取(xi，yi)右方象素(xi＋1，yi)。

二、区域填充算法

1、递归算法

从指定的种子点开始，向各个方向上搜索，逐个像素进行处理，直到遇到边界，各种种子填充算法只是在处理颜色和边界的方式上有所不同。

2、扫描线算法

扫描线种子填充算法的基本过程如下：当给定种子点(x, y)时，首先分别向左和向右两个方向填充种子点所在扫描线上的位于给定区域的一个区段，同时记下这个区段的范围[xLeft, xRight]，然后确定与这一区段相连通的上、下两条扫描线上位于给定区域内的区段，并依次保存下来。反复这个过程，直到填充结束。

扫描线种子填充算法可由下列四个步骤实现：

(1) 初始化一个空的栈用于存放种子点，将种子点(x, y)入栈；

(2) 判断栈是否为空，如果栈为空则结束算法，否则取出栈顶元素作为当前扫描线的种子点(x, y)，y是当前的扫描线；

(3) 从种子点(x,y)出发，沿当前扫描线向左、右两个方向填充，直到边界。分别标记区段的左、右端点坐标为xLeft和xRight；

(4) 分别检查与当前扫描线相邻的y - 1和y + 1两条扫描线在区间[xLeft,xRight]中的像素，从xLeft开始向xRight方向搜索，若存在非边界且未填充的像素点，则找出这些相邻的像素点中最右边的一个，并将其作为种子点压入栈中，然后返回第（2）步；

三、算法实现

总结及学习感悟

在学习直线扫描算法时，一开始总是画不出来，后来发现这句glBegin(GL_POINTS);少了个S，没有S就只能画一个点，细节很重要。

学习区域填充算法时，基本的思路就是以一个点为起点，不断探索周围，如果在这个区域内，就填充颜色，如果遇到边界就停止。扫描线算法也是，先以某点画一条直线，在区域内的线段部分就填充颜色。

我们就像被选中的一点一样，周围的一切对我们来说都是不可知的黑色，只有不断探索，才知道哪里是边界，也可能或许没有边界，或许边界的那边又是一个更大的新世界······噗，我想多了。

源代码

扫描线主要算法

void k1() //0<k<1
{
 glClear(GL_COLOR_BUFFER_BIT); 

 glColor3f(0.0,0.0,0.0);
 glBegin(GL_POINTS);
 GLint x1=0,y1=0,x2=400,y2=200;
 GLint x=x1,y=y1;
 GLint dx=x2-x1,dy=y2-y1,dT=2*(dy-dx),dS=2*dy;
 GLint d=2*dy-dx;
 glVertex2i(x,y);
 while(x<x2)
 {
 x++;
 if(d<0)
 d=d+dS;
 else
 {
 y++;
 d=d+dT;
 }
 glVertex2i(x,y);
 }
 glEnd();
 glFlush(); 

}

区域填充
#include "gl/glut.h"
#include "windows.h"
const int POINTNUM=7; //多边形点数.

/******定义结构体用于活性边表AET和新边表NET***********************************/
 typedef struct XET
 {
 float x;
 float dx,ymax;
 XET* next;
 }AET,NET;

/******定义点结构体point******************************************************/
 struct point
 {
 float x;
 float y;
 }
 polypoint[POINTNUM]={250,50,550,150,550,400,250,250,100,350,100,100,120,30};//多边形顶点

 void PolyScan()
{
/******计算最高点的y坐标(扫描到此结束)****************************************/
 int MaxY=0;
 int i;
 for(i=0;i<POINTNUM;i++)
 if(polypoint[i].y>MaxY)
 MaxY=polypoint[i].y;

/*******初始化AET表***********************************************************/
 AET *pAET=new AET;
 pAET->next=NULL;

/******初始化NET表************************************************************/
 NET *pNET[1024];
 for(i=0;i<=MaxY;i++)
 {
 pNET[i]=new NET;
 pNET[i]->next=NULL;
 }
 glClear(GL_COLOR_BUFFER_BIT); //赋值的窗口显示.
 glColor3f(0.0,0.0,0.0);  //设置直线的颜色红色
 glBegin(GL_POINTS);
/******扫描并建立NET表*********************************************************/
 for(i=0;i<=MaxY;i++)
 {
 for(int j=0;j<POINTNUM;j++)
 if(polypoint[j].y==i)
 { //一个点跟前面的一个点形成一条线段，跟后面的点也形成线段
 if(polypoint[(j-1+POINTNUM)%POINTNUM].y>polypoint[j].y)
 {
 NET *p=new NET;
 p->x=polypoint[j].x;
 p->ymax=polypoint[(j-1+POINTNUM)%POINTNUM].y;
 p->dx=(polypoint[(j-1+POINTNUM)%POINTNUM].x-polypoint[j].x)/(polypoint[(j-1+POINTNUM)%POINTNUM].y-polypoint[j].y);
 p->next=pNET[i]->next;
 pNET[i]->next=p;

 }
 if(polypoint[(j+1+POINTNUM)%POINTNUM].y>polypoint[j].y)
 {
 NET *p=new NET;
 p->x=polypoint[j].x;
 p->ymax=polypoint[(j+1+POINTNUM)%POINTNUM].y;
 p->dx=(polypoint[(j+1+POINTNUM)%POINTNUM].x-polypoint[j].x)/(polypoint[(j+1+POINTNUM)%POINTNUM].y-polypoint[j].y);
 p->next=pNET[i]->next;
 pNET[i]->next=p;
 }
 }
 }
/******建立并更新活性边表AET*****************************************************/
for(i=0;i<=MaxY;i++)
 {
 //计算新的交点x,更新AET
 NET *p=pAET->next;
 while(p)
 {
 p->x=p->x + p->dx;
 p=p->next;
 }
 //更新后新AET先排序*************************************************************/
 //断表排序,不再开辟空间
 AET *tq=pAET;
 p=pAET->next;
 tq->next=NULL;
 while(p)
 {
 while(tq->next && p->x >= tq->next->x)
 tq=tq->next;
 NET *s=p->next;
 p->next=tq->next;
 tq->next=p;
 p=s;
 tq=pAET;
 }
 //(改进算法)先从AET表中删除ymax==i的结点****************************************/
 AET *q=pAET;
 p=q->next;
 while(p)
 {
 if(p->ymax==i)
 {
 q->next=p->next;
 delete p;
 p=q->next;
 }
 else
 {
 q=q->next;
 p=q->next;
 }
 }
 //将NET中的新点加入AET,并用插入法按X值递增排序**********************************/
 p=pNET[i]->next;
 q=pAET;
 while(p)
 {
 while(q->next && p->x >= q->next->x)
 q=q->next;
 NET *s=p->next;
 p->next=q->next;
 q->next=p;
 p=s;
 q=pAET;
 }
/******配对填充颜色***************************************************************/

  p=pAET->next;
 while(p && p->next)
 {
 for(float j=p->x;j<=p->next->x;j++)
 glVertex2i(static_cast<int>(j),i);
 p=p->next->next;//考虑端点情况
 }

 }
 glEnd();
glFlush();
}
void init(void)
{glClearColor(1.0,1.0,1.0,0.0);
//窗口的背景颜色设置为白色
glMatrixMode(GL_PROJECTION);
gluOrtho2D(0.0,600.0,0.0,450.0);
}

void main(int argc,char* argv)
{
 glutInit(&argc,&argv);  //I初始化 GLUT.
 glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB); //设置显示模式：单个缓存和使用RGB模型
 glutInitWindowPosition(50,100); //设置窗口的顶部和左边位置
 glutInitWindowSize(400,300); //设置窗口的高度和宽度
 glutCreateWindow("An Example OpenGL Program"); //创建显示窗口

 init();    //调用初始化过程
 glutDisplayFunc(PolyScan); //图形的定义传递给我window.
 glutMainLoop();   //显示所有的图形并等待
 }

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。