基于Python共轭梯度法与最速下降法之间的对比

在一般问题的优化中，最速下降法和共轭梯度法都是非常有用的经典方法，但最速下降法往往以”之”字形下降，速度较慢，不能很快的达到最优值，共轭梯度法则优于最速下降法，在前面的某个文章中，我们给出了牛顿法和最速下降法的比较，牛顿法需要初值点在最优点附近，条件较为苛刻。

算法来源：《数值最优化方法》高立，P111

我们选用了64维的二次函数来作为验证函数，具体参见上书111页。

采用的三种方法为：

共轭梯度方法（FR格式）、共轭梯度法（PRP格式）、最速下降法

# -*- coding: utf-8 -*-
"""
Created on Sat Oct 01 15:01:54 2016
@author: zhangweiguo
"""
import sympy,numpy
import math
import matplotlib.pyplot as pl
from mpl_toolkits.mplot3d import Axes3D as ax3
import SD#这个文件里有最速下降法SD的方法，参见前面的博客
#共轭梯度法FR、PRP两种格式
def CG_FR(x0,N,E,f,f_d):
  X=x0;Y=[];Y_d=[];
  n = 1
  ee = f_d(x0)
  e=(ee[0]**2+ee[1]**2)**0.5
  d=-f_d(x0)
  Y.append(f(x0)[0,0]);Y_d.append(e)
  a=sympy.Symbol('a',real=True)
  print '第%2s次迭代：e=%f' % (n, e)
  while n<N and e>E:
    n=n+1
    g1=f_d(x0)
    f1=f(x0+a*f_d(x0))
    a0=sympy.solve(sympy.diff(f1[0,0],a,1))
    x0=x0-d*a0
    X=numpy.c_[X,x0];Y.append(f(x0)[0,0])
    ee = f_d(x0)
    e = math.pow(math.pow(ee[0,0],2)+math.pow(ee[1,0],2),0.5)
    Y_d.append(e)
    g2=f_d(x0)
    beta=(numpy.dot(g2.T,g2))/numpy.dot(g1.T,g1)
    d=-f_d(x0)+beta*d
    print '第%2s次迭代：e=%f'%(n,e)
  return X,Y,Y_d
def CG_PRP(x0,N,E,f,f_d):
  X=x0;Y=[];Y_d=[];
  n = 1
  ee = f_d(x0)
  e=(ee[0]**2+ee[1]**2)**0.5
  d=-f_d(x0)
  Y.append(f(x0)[0,0]);Y_d.append(e)
  a=sympy.Symbol('a',real=True)
  print '第%2s次迭代：e=%f' % (n, e)
  while n<N and e>E:
    n=n+1
    g1=f_d(x0)
    f1=f(x0+a*f_d(x0))
    a0=sympy.solve(sympy.diff(f1[0,0],a,1))
    x0=x0-d*a0
    X=numpy.c_[X,x0];Y.append(f(x0)[0,0])
    ee = f_d(x0)
    e = math.pow(math.pow(ee[0,0],2)+math.pow(ee[1,0],2),0.5)
    Y_d.append(e)
    g2=f_d(x0)
    beta=(numpy.dot(g2.T,g2-g1))/numpy.dot(g1.T,g1)
    d=-f_d(x0)+beta*d
    print '第%2s次迭代：e=%f'%(n,e)
  return X,Y,Y_d
if __name__=='__main__':
  '''
  G=numpy.array([[21.0,4.0],[4.0,15.0]])
  #G=numpy.array([[21.0,4.0],[4.0,1.0]])
  b=numpy.array([[2.0],[3.0]])
  c=10.0
  x0=numpy.array([[-10.0],[100.0]])
  '''

  m=4
  T=6*numpy.eye(m)
  T[0,1]=-1;T[m-1,m-2]=-1
  for i in xrange(1,m-1):
    T[i,i+1]=-1
    T[i,i-1]=-1
  W=numpy.zeros((m**2,m**2))
  W[0:m,0:m]=T
  W[m**2-m:m**2,m**2-m:m**2]=T
  W[0:m,m:2*m]=-numpy.eye(m)
  W[m**2-m:m**2,m**2-2*m:m**2-m]=-numpy.eye(m)
  for i in xrange(1,m-1):
    W[i*m:(i+1)*m,i*m:(i+1)*m]=T
    W[i*m:(i+1)*m,i*m+m:(i+1)*m+m]=-numpy.eye(m)
    W[i*m:(i+1)*m,i*m-m:(i+1)*m-m]=-numpy.eye(m)
  mm=m**2
  mmm=m**3
  G=numpy.zeros((mmm,mmm))
  G[0:mm,0:mm]=W;G[mmm-mm:mmm,mmm-mm:mmm]=W;
  G[0:mm,mm:2*mm]=-numpy.eye(mm)
  G[mmm-mm:mmm,mmm-2*mm:mmm-mm]=-numpy.eye(mm)
  for i in xrange(1,m-1):
    G[i*mm:(i+1)*mm,i*mm:(i+1)*mm]=W
    G[i*mm:(i+1)*mm,i*mm-mm:(i+1)*mm-mm]=-numpy.eye(mm)
    G[i*mm:(i+1)*mm,i*mm+mm:(i+1)*mm+mm]=-numpy.eye(mm)
  x_goal=numpy.ones((mmm,1))
  b=-numpy.dot(G,x_goal)
  c=0
  f = lambda x: 0.5 * (numpy.dot(numpy.dot(x.T, G), x)) + numpy.dot(b.T, x) + c
  f_d = lambda x: numpy.dot(G, x) + b
  x0=x_goal+numpy.random.rand(mmm,1)*100
  N=100
  E=10**(-6)
  print '共轭梯度PR'
  X1, Y1, Y_d1=CG_FR(x0,N,E,f,f_d)
  print '共轭梯度PBR'
  X2, Y2, Y_d2=CG_PRP(x0,N,E,f,f_d)
  figure1=pl.figure('trend')
  n1=len(Y1)
  n2=len(Y2)
  x1=numpy.arange(1,n1+1)
  x2=numpy.arange(1,n2+1)

  X3, Y3, Y_d3=SD.SD(x0,N,E,f,f_d)
  n3=len(Y3)
  x3=range(1,n3+1)
  pl.semilogy(x3,Y3,'g*',markersize=10,label='SD:'+str(n3))
  pl.semilogy(x1,Y1,'r*',markersize=10,label='CG-FR:'+str(n1))
  pl.semilogy(x2,Y2,'b*',markersize=10,label='CG-PRP:'+str(n2))
  pl.legend()
  #图像显示了三种不同的方法各自迭代的次数与最优值变化情况，共轭梯度方法是明显优于最速下降法的
  pl.xlabel('n')
  pl.ylabel('f(x)')
  pl.show()

最优值变化趋势：

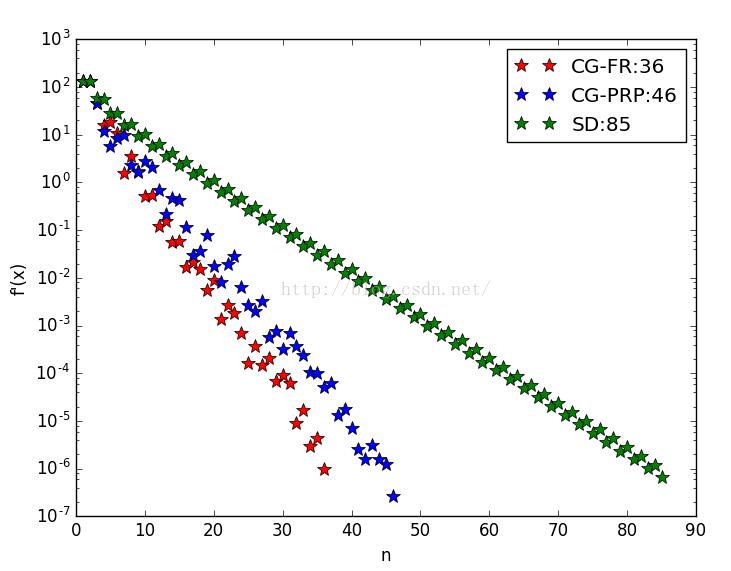
从图中可以看出，最速下降法SD的迭代次数是最多的，在与共轭梯度（FR与PRP两种方法）的比较中，明显较差。

补充知识：python实现牛顿迭代法和二分法求平方根，精确到小数点后无限多位-4

首先来看一下牛顿迭代法求平方根的过程：计算3的平方根

如图，是求根号3的牛顿迭代法过程。这里使用的初始迭代值（也就是猜测值）为1，其实可以为任何值最终都能得到结果。每次开始，先检测猜测值是否合理，不合理时，用上面的平均值来换掉猜测值，依次继续迭代，直到猜测值合理。

原理：现在取一个猜测值 a, 如果猜测值合理的话，那么就有a^2=x，即x/a=a ,x为被开方数。不合理的话呢，就用表中的猜测值和商的平均值来换掉猜测值。当不合理时，比如 a>真实值，那么x/a<真实值，这时候取a 与 x/a 的平均值来代替a的话，那么新的a就会比原来的a要更接近真实值。同理有 a<真实值 的情况。于是，这样不断迭代下去最终是一个a不断收敛到真实值的一个过程。于是不断迭代就能得到真实值，证明了迭代法是正确的。

附上我的python代码：

利用python整数运算，python整数可以无限大，可以实现小数点后无限多位

#二分法求x的平方根小数点下任意K位数的精准值，利用整数运算 #思想：利用二分法，每次乘以10，取中间值，比较大小，从而定位精确值的范围，将根扩大10倍，则被开方数扩大100倍。 #quotient（商）牛顿迭代法：先猜测一个值，再求商，然后用猜测值和商的中间值代替猜测值，扩大倍数，继续进行。

import math
from math import sqrt

def check_precision(l,h,p,len1):#检查是否达到了精确位
  l=str(l);h=str(h)
  if len(l)<=len1+p or len(h)<=len1+p:
    return False
  for i in range(len1,p+len1):#检查小数点后面的p个数是否相等
    if l[i]!=h[i]:     #当l和h某一位不相等时，说明没有达到精确位
      return False
  return True

def print_result(x,len1,p):
  x=str(x)
  if len(x)-len1<p:#没有达到要求的精度就已经找出根
    s=x[:len1]+"."+x[len1:]+'0'*(p-len(x)+len1)
  else:s=x[:len1]+"."+x[len1:len1+p]
  print(s)

def binary_sqrt(x,p):
  x0=int(sqrt(x))
  if x0*x0==x: #完全平方数直接开方，不用继续进行
    print_result(x0,len(str(x0)),p)
    return
  len1=len(str(x0))#找出整数部分的长度
  l=0;h=x
  while(not check_precision(l,h,p,len1)):#没有达到精确位，继续循环
    if not l==0:#第一次l=0，h=x时不用乘以10，直接取中间值
      h=h*10 #l,h每次扩大10倍
      l=l*10
      x=x*100 #x每次要扩大100倍，因为平方
    m=(l+h)//2
    if m*m==x:
      return print_result(m,len1,p)
    elif m*m>x:
      h=m
    else:
      l=m
  return print_result(l,len1,p)#当达到了要求的精度，直接返回l

#牛顿迭代法求平方根
def newton_sqrt(x,p):
  x0=int(sqrt(x))
  if x0*x0==x: #完全平方数直接开方，不用继续进行
    print_result(x0,len(str(x0)),p)
    return
  len1=len(str(x0))#找出整数部分的长度
  g=1;q=x//g;g=(g+q)//2
  while(not check_precision(g,q,p,len1)):
    x=x*100
    g=g*10
    q=x//g   #求商
    g=(g+q)//2 #更新猜测值为猜测值和商的中间值
  return print_result(g,len1,p)

while True:
  x=int(input("请输入待开方数："))
  p=int(input("请输入精度："))
  print("binary_sqrt:",end="")
  binary_sqrt(x,p)
  print("newton_sqrt:",end="")
  newton_sqrt(x,p)

以上这篇基于Python共轭梯度法与最速下降法之间的对比就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。