Python深度学习pyTorch权重衰减与L2范数正则化解析

2024-10-11 04:14:08

下面进行一个高维线性实验

假设我们的真实方程是：

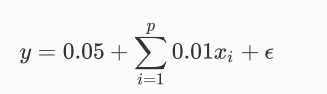
假设feature数200，训练样本和测试样本各20个

模拟数据集

num_train,num_test = 10,10
num_features = 200
true_w = torch.ones((num_features,1),dtype=torch.float32) * 0.01
true_b = torch.tensor(0.5)
samples = torch.normal(0,1,(num_train+num_test,num_features))
noise = torch.normal(0,0.01,(num_train+num_test,1))
labels = samples.matmul(true_w) + true_b + noise
train_samples, train_labels= samples[:num_train],labels[:num_train]
test_samples, test_labels = samples[num_train:],labels[num_train:]

定义带正则项的loss function

def loss_function(predict,label,w,lambd):
    loss = (predict - label) ** 2
    loss = loss.mean() + lambd * (w**2).mean()
    return loss

画图的方法

def semilogy(x_val,y_val,x_label,y_label,x2_val,y2_val,legend):
    plt.figure(figsize=(3,3))
    plt.xlabel(x_label)
    plt.ylabel(y_label)
    plt.semilogy(x_val,y_val)
    if x2_val and y2_val:
        plt.semilogy(x2_val,y2_val)
        plt.legend(legend)
    plt.show()

拟合和画图

def fit_and_plot(train_samples,train_labels,test_samples,test_labels,num_epoch,lambd):
    w = torch.normal(0,1,(train_samples.shape[-1],1),requires_grad=True)
    b = torch.tensor(0.,requires_grad=True)
    optimizer = torch.optim.Adam([w,b],lr=0.05)
    train_loss = []
    test_loss = []
    for epoch in range(num_epoch):
        predict = train_samples.matmul(w) + b
        epoch_train_loss = loss_function(predict,train_labels,w,lambd)
        optimizer.zero_grad()
        epoch_train_loss.backward()
        optimizer.step()
        test_predict = test_sapmles.matmul(w) + b
        epoch_test_loss = loss_function(test_predict,test_labels,w,lambd)
        train_loss.append(epoch_train_loss.item())
        test_loss.append(epoch_test_loss.item())
    semilogy(range(1,num_epoch+1),train_loss,'epoch','loss',range(1,num_epoch+1),test_loss,['train','test'])

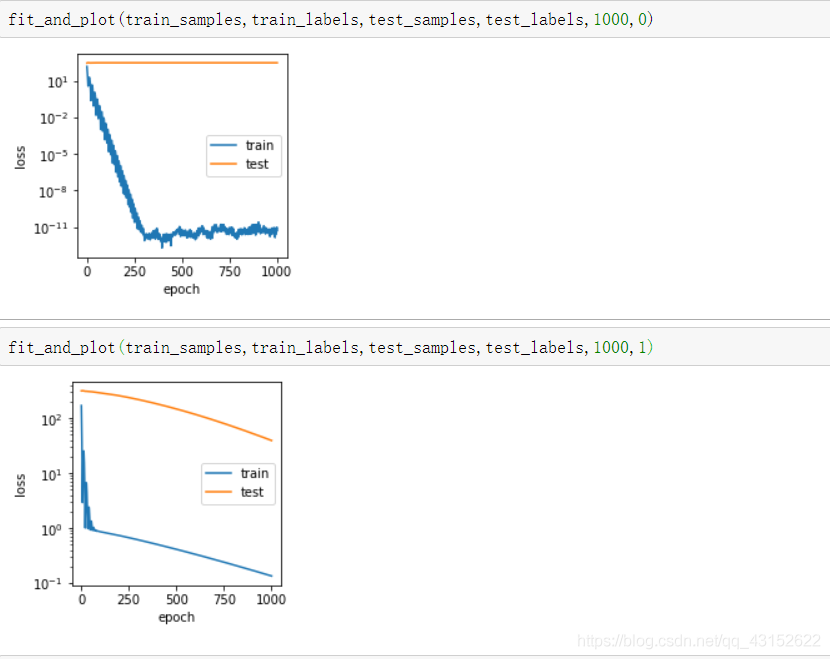
可以发现加了正则项的模型，在测试集上的loss确实下降了

以上就是Python深度学习pyTorch权重衰减与L2范数正则化解析的详细内容，更多关于Python pyTorch权重与L2范数正则化的资料请关注我们其它相关文章！

在Pytorch中使用样本权重(sample_weight)的正确方法

step: 1.将标签转换为one-hot形式. 2.将每一个one-hot标签中的1改为预设样本权重的值即可在Pytorch中使用样本权重. eg: 对于单个样本:loss = - Q * log(P),如下: P = [0.1,0.2,0.4,0.3] Q = [0,0,1,0] loss = -Q * np.log(P) 增加样本权重则为loss = - Q * log(P) *sample_weight P = [0.1,0.2,0.4,0.3] Q = [0,0,sample_wei
PyTorch 实现L2正则化以及Dropout的操作

了解知道Dropout原理如果要提高神经网络的表达或分类能力,最直接的方法就是采用更深的网络和更多的神经元,复杂的网络也意味着更加容易过拟合. 于是就有了Dropout,大部分实验表明其具有一定的防止过拟合的能力. 用代码实现Dropout Dropout的numpy实现 PyTorch中实现dropout import torch.nn.functional as F import torch.nn.init as init import torch from torch.autograd
Pytorch中的数据集划分&正则化方法

1.训练集&验证集&测试集训练集:训练数据验证集:验证不同算法(比如利用网格搜索对超参数进行调整等),检验哪种更有效测试集:正确评估分类器的性能正常流程:验证集会记录每个时间戳的参数,在加载test数据前会加载那个最好的参数,再来评估.比方说训练完6000个epoch后,发现在第3520个epoch的validation表现最好,测试时会加载第3520个epoch的参数. import torch import torch.nn as nn import torch.nn.func
Pytorch 如何实现常用正则化

Stochastic Depth 论文:Deep Networks with Stochastic Depth 本文的正则化针对于ResNet中的残差结构,类似于dropout的原理,训练时对模块进行随机的删除,从而提升模型的泛化能力. 对于上述的ResNet网络,模块越在后面被drop掉的概率越大. 作者直觉上认为前期提取的低阶特征会被用于后面的层. 第一个模块保留的概率为1,之后保留概率随着深度线性递减. 对一个模块的drop函数可以采用如下的方式实现: def drop_connect(i
Python深度学习pyTorch权重衰减与L2范数正则化解析

下面进行一个高维线性实验假设我们的真实方程是: 假设feature数200,训练样本和测试样本各20个模拟数据集 num_train,num_test = 10,10 num_features = 200 true_w = torch.ones((num_features,1),dtype=torch.float32) * 0.01 true_b = torch.tensor(0.5) samples = torch.normal(0,1,(num_train+num_test,num_fe
Python深度学习pytorch神经网络Dropout应用详解解

目录扰动的鲁棒性实践中的dropout 简洁实现扰动的鲁棒性在之前我们讨论权重衰减(L2正则化)时看到的那样,参数的范数也代表了一种有用的简单性度量.简单性的另一个有用角度是平滑性,即函数不应该对其输入的微笑变化敏感.例如,当我们对图像进行分类时,我们预计向像素添加一些随机噪声应该是基本无影响的. dropout在正向传播过程中,计算每一内部层同时注入噪声,这已经成为训练神经网络的标准技术.这种方法之所以被称为dropout,因为我们从表面上看是在训练过程中丢弃(drop out)一些
Python深度学习pytorch神经网络图像卷积运算详解

目录互相关运算卷积层特征映射由于卷积神经网络的设计是用于探索图像数据,本节我们将以图像为例. 互相关运算严格来说,卷积层是个错误的叫法,因为它所表达的运算其实是互相关运算(cross-correlation),而不是卷积运算.在卷积层中,输入张量和核张量通过互相关运算产生输出张量. 首先,我们暂时忽略通道(第三维)这一情况,看看如何处理二维图像数据和隐藏表示.下图中,输入是高度为3.宽度为3的二维张量(即形状为 3 × 3 3\times3 3×3).卷积核的高度和宽度都是2. 注意,
Python深度学习pytorch卷积神经网络LeNet

目录 LeNet 模型训练在本节中,我们将介绍LeNet,它是最早发布的卷积神经网络之一.这个模型是由AT&T贝尔实验室的研究院Yann LeCun在1989年提出的(并以其命名),目的是识别手写数字.当时,LeNet取得了与支持向量机性能相媲美的成果,成为监督学习的主流方法.LeNet被广泛用于自动取款机中,帮助识别处理支票的数字. LeNet 总体来看,LeNet(LeNet-5)由两个部分组成: 卷积编码器: 由两个卷积层组成全连接层密集快: 由三个全连接层组成每个卷积块中的基本单元
Python深度学习pytorch神经网络填充和步幅的理解

目录填充步幅上图中,输入的高度和宽度都为3,卷积核的高度和宽度都为2,生成的输出表征的维度为 2 × 2 2\times2 2×2.从上图可看出卷积的输出形状取决于输入形状和卷积核的形状. 填充以上面的图为例,在应用多层卷积时,我们常常丢失边缘像素. 解决这个问题的简单方法即为填充(padding):在输入图像的边界填充元素(通常填充元素是0). 例如,在上图中我们将 3 × 3 3\times3 3×3输入填充到 5 × 5 5\times5 5×5,那么它的输出就增加为 4 × 4
Python深度学习pytorch神经网络多输入多输出通道

目录多输入通道多输出通道 1 × 1 1\times1 1×1卷积层虽然每个图像具有多个通道和多层卷积层.例如彩色图像具有标准的RGB通道来指示红.绿和蓝.但是到目前为止,我们仅展示了单个输入和单个输出通道的简化例子.这使得我们可以将输入.卷积核和输出看作二维张量. 当我们添加通道时,我们的输入和隐藏的表示都变成了三维张量.例如,每个RGB输入图像具有 3 × h × w 3\times{h}\times{w} 3×h×w的形状.我们将这个大小为3的轴称为通道(channel)维度.在本节
Python深度学习pytorch神经网络汇聚层理解

目录最大汇聚层和平均汇聚层填充和步幅多个通道我们的机器学习任务通常会跟全局图像的问题有关(例如,"图像是否包含一只猫呢?"),所以我们最后一层的神经元应该对整个输入的全局敏感.通过逐渐聚合信息,生成越来越粗糙的映射,最终实现学习全局表示的目标,同时将卷积图层的所有有时保留在中间层. 此外,当检测较底层的特征时(例如之前讨论的边缘),我们通常希望这些特征保持某种程度上的平移不变性.例如,如果我们拍摄黑白之间轮廓清晰的图像X,并将整个图像向右移动一个像素,即Z[i, j] = X[
Python深度学习pytorch神经网络多层感知机简洁实现

我们可以通过高级API更简洁地实现多层感知机. import torch from torch import nn from d2l import torch as d2l 模型与softmax回归的简洁实现相比,唯一的区别是我们添加了2个全连接层.第一层是隐藏层,它包含256个隐藏单元,并使用了ReLU激活函数.第二层是输出层. net = nn.Sequential(nn.Flatten(), nn.Linear(784, 256), nn.ReLU(), nn.Linear(256, 1
Python深度学习pytorch实现图像分类数据集

目录读取数据集读取小批量整合所有组件目前广泛使用的图像分类数据集之一是MNIST数据集.如今,MNIST数据集更像是一个健全的检查,而不是一个基准. 为了提高难度,我们将在接下来的章节中讨论在2017年发布的性质相似但相对复杂的Fashion-MNIST数据集. import torch import torchvision from torch.utils import data from torchvision import transforms from d2l import to
Python深度学习pytorch神经网络块的网络之VGG

目录 VGG块 VGG网络训练模型与芯片设计中工程师从放置晶体管到逻辑元件再到逻辑块的过程类似,神经网络结构的设计也逐渐变得更加抽象.研究人员开始从单个神经元的角度思考问题,发展到整个层次,现在又转向模块,重复各层的模式. 使用块的想法首先出现在牛津大学的视觉几何组(visualgeometry Group)(VGG)的VGG网络中.通过使用循环和子程序,可以很容易地在任何现代深度学习框架的代码中实现这些重复的结构. VGG块经典卷积神经网络的基本组成部分是下面的这个序列: 1.带填充以保

Python深度学习pyTorch权重衰减与L2范数正则化解析

模拟数据集

定义带正则项的loss function

画图的方法

拟合和画图

相关推荐

随机推荐