Java 数据结构与算法系列精讲之KMP算法

2024-07-29 05:14:03

概述

从今天开始, 小白我将带大家开启 Java 数据结构 & 算法的新篇章.

KMP 算法

KMP (Knuth-Morris-Pratt), 是一种改进的字符串匹配算法. KMP 算法解决了暴力匹配需要高频回退的问题, KMP 算法在匹配上若干字符后, 字符串位置不需要回退, 从而大大提高效率. 如图:

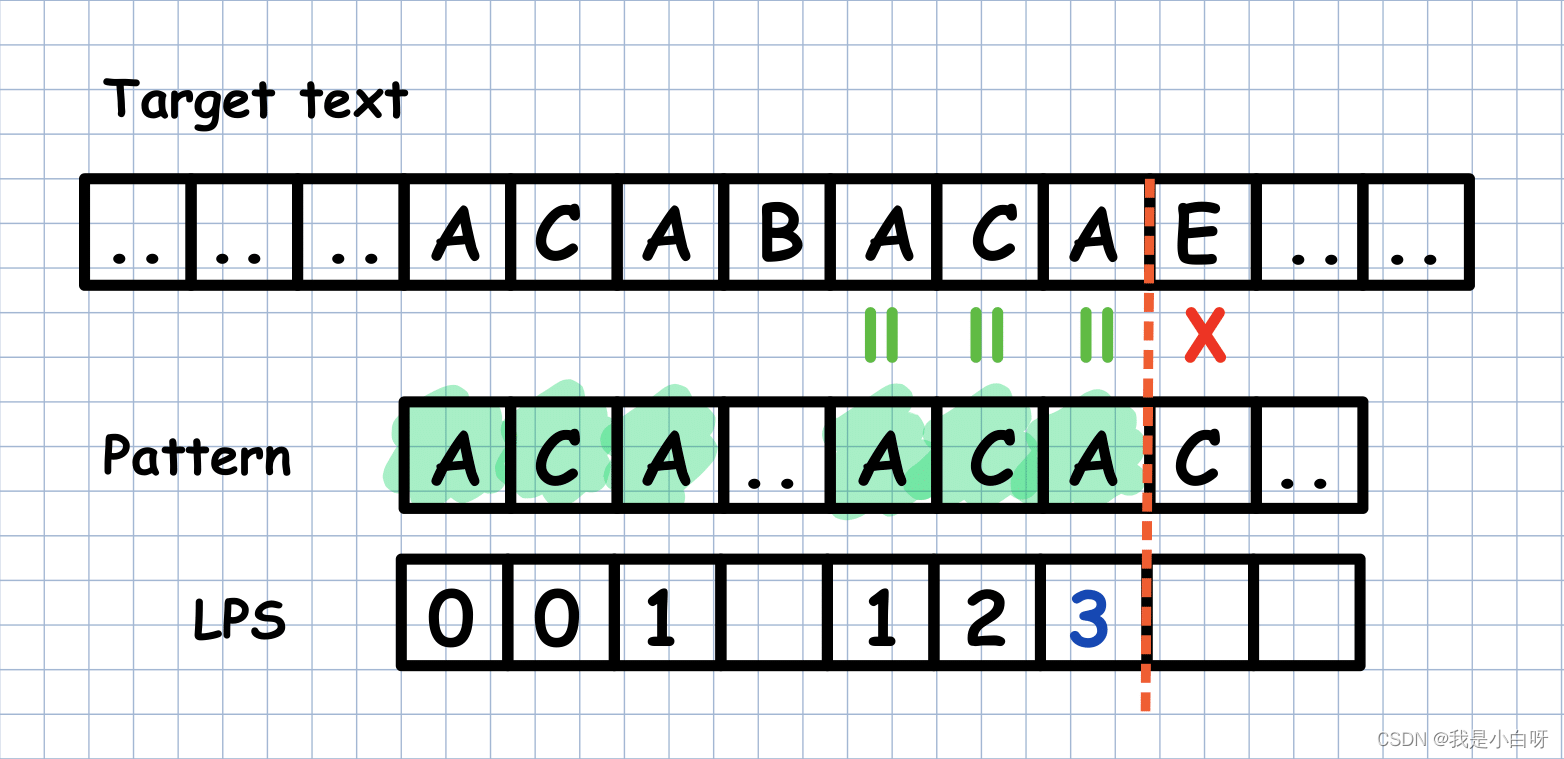
举个例子 (字符串 “abcabcdef” 匹配字符串 “abcdef”):

次数	暴力匹配	KMP 算法	说明
1	`a`bcabcdef `a`bcdef	`a`bcabcdef `a`bcdef	a 和 a 匹配
2	`ab`cabcdef `ab`cdef	`ab`cabcdef `ab`cdef	ab 和 ab 匹配
3	`abc`abcdef `abc`def	`abc`abcdef `abc`def	abc 和 abc 匹配
4	abc`a`bcdef abc`d`ef	abc`a`bcdef abc`d`ef	abca 和 abcd 不匹配, 回退. 暴力匹配回退到索引 1, 即 “b”, KMP 算法索引跳置 3, 即 “a”
5	a`b`cabcdef `a`bcdef	abc`a`bcdef `a`bcdef	暴力匹配 b 和 a 不匹配, 后移. KMP 算法 a 和 a 匹配
6	ab`c`abcdef `a`bcdef	abc`ab`cdef `ab`cdef	暴力匹配 c 和 a 不匹配, 后移. KMP 算法 ab 和 ab 匹配
7	abc`a`bcdef `a`bcdef	abc`abc`def `abc`def	暴力匹配 a 和 a 匹配. KMP 算法 abc 和 abc 匹配
8	abc`ab`cdef `ab`cdef	abc`abcd`ef `abcd`ef	暴力匹配 ab 和 ab 匹配. KMP 算法 abcd 和 abcd 匹配
9	abc`abc`def `abc`def	abc`abcde`f `abcde`f	暴力匹配 abc 和 abc 匹配. KMP 算法 abcde 和 abcde 匹配
10	abc`abcd`ef `abcd`ef	abc`abcdef abcdef`	暴力匹配 abcd 和 abcd 匹配. KMP 算法 abcdef 和 abcdef 匹配 , 匹配完成
11	abc`abcde`f `abcde`f	abc`abcdef abcdef`	暴力匹配 abcde 和 abcde 匹配. KMP 算法匹配完成
12	abc`abcdef abcdef`	abc`abcdef abcdef`	暴力匹配 abcd 和 abcd 匹配, 匹配完成. KMP 算法匹配完成

部分匹配表

部分匹配表 (Partial Match Table) 指的是 “前缀” 和 “后缀” 的最长共有元素的长度.

举个例子, 字符串 “ABCDABD” 的前缀与后缀:

字符串	前缀	后缀	共同部分	值
A	NaN	NaN	NaN	0
AB	A	B	NaN	0
ABC	A, AB	C, BC	NaN	0
ABCD	A, AB, ABC	D, CD, BCD	NaN	0
ABCDA	A, AB, ABC, ABCD	A, DA, CDA, BCDA	A	1
ABCDAB	A, AB, ABC, ABCD, ABCDA	B, AB, DAB, CDAB, BCDAB	AB	2
ABCDAB	A, AB, ABC, ABCD, ABCDA, ABCDAB	D, BD, ABD, DABD, CDABD, BCDABD	NaN	0

KMP 算法实现

重点:

KMP 算法中移动的位数 = 已匹配的字符数 - 对应的部分匹配值

import java.util.Arrays;

public class KMPMatch {

    public static int Match(String str1, String str2, int[] next) {

        // 初始化索引
        int i = 0;
        int j = 0;

        for (; i < str1.length(); i++) {

            if (j > 0 && str1.charAt(i) != str2.charAt(j)) {
                // 不匹配, 回退
                i = i - next[j - 1];
                j = 0;
            }

            // 匹配
            if (str1.charAt(i) == str2.charAt(j)) {
                j++;
            }

            // 返回索引
            if (j == str2.length()) {
                return i - j + 1;
            }
        }
        return -1;
    }

    // 部分匹配
    public static int[] getNext(String s) {

        // 定义数组
        int next[] = new int[s.length()];

        // 初始化i, j
        int i = 0;
        int j = -1;
        next[0] = -1;

        // 遍历
        while (i < s.length() - 1) {
            if (j == -1 || s.charAt(i) == s.charAt(j)) {
                // 匹配成功
                next[i] = j + 1;
                i++;
                j++;
            } else {
                //一旦不匹配成功j回退到-1
                j = -1;
            }
        }
        return next;
    }

    public static void main(String[] args) {

        // 字符串1
        String str1 = "BBCABCDAB ABCDABD";

        // 字符串2
        String str2 = "ABCDABD";

        // 匹配表
        int[] next = getNext(str2);
        System.out.println(Arrays.toString(next));

        // KMP算法
        int result = Match(str1, str2, next);
        System.out.println(result);
    }
}

输出结果:

[0, 0, 0, 0, 1, 2, 0]
10

到此这篇关于Java 数据结构与算法系列精讲之KMP算法的文章就介绍到这了,更多相关Java KMP 算法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

java暴力匹配及KMP算法解决字符串匹配问题示例详解

目录要解决的问题? 一.暴力匹配算法一个图例介绍KMP算法二.KMP算法算法介绍一个图例介绍KMP算法代码实现要解决的问题? 一.暴力匹配算法一个图例介绍KMP算法 String str1 = "BBC ABCDAB ABCDABCDABDE"; String str2 = "ABCDABD"; 1. S[0]为B,P[0]为A,不匹配,执行第②条指令:"如果失配(即S[i]! = P[j]),令i = i - (j - 1),
Java 数据结构与算法系列精讲之字符串暴力匹配

概述从今天开始, 小白我将带大家开启 Java 数据结构 & 算法的新篇章. 字符串匹配字符串匹配 (String Matching) 指的是判断一个字符串是否包含另一个字符串. 举个例子: 字符串 "Hello World" 包含字符串 "Hello" 字符串 "Hello World" 不包含字符串 "LaLaLa" 暴力匹配暴力匹配 (Brute-Force) 的思路: 如果charArray1[i] ==
Java 数据结构与算法系列精讲之排序算法

概述从今天开始, 小白我将带大家开启 Java 数据结构 & 算法的新篇章. 冒泡排序冒泡排序 (Bubble Sort) 是一种简单的排序算法. 它重复地遍历要排序的数列, 一次比较两个元素, 如果他们的顺序错误就把他们交换过来. 遍历数列的工作是重复地进行直到没有再需要交换, 也就是说该数列已经排序完成. 这个算法的名字由来是因为越小的元素会经由交换慢慢 "浮" 到数列的顶端. 冒泡排序流程: 通过比较相邻的元素, 判断两个元素位置是否需要互换进行 n-1 次比较,
Java 数据结构与算法系列精讲之贪心算法

概述从今天开始, 小白我将带大家开启 Java 数据结构 & 算法的新篇章. 贪心算法贪心算法 (Greedy Algorithm) 指的是在每一步选择中都采取在当前状态下最好或最优的选择, 从而希望导致结果是最好或最优的算法. 贪心算法锁得到的结果不一定是最优的结果, 但是都是相对近似最优的结果. 贪心算法的优缺点: 优点: 贪心算法的代码十分简单缺点: 很难确定一个问题是否可以用贪心算法解决电台覆盖问题假设存在以下的广播台, 以及广播台可以覆盖的地区: 广播台覆盖地区 K1 北京
Java 数据结构与算法系列精讲之KMP算法

概述从今天开始, 小白我将带大家开启 Java 数据结构 & 算法的新篇章. KMP 算法 KMP (Knuth-Morris-Pratt), 是一种改进的字符串匹配算法. KMP 算法解决了暴力匹配需要高频回退的问题, KMP 算法在匹配上若干字符后, 字符串位置不需要回退, 从而大大提高效率. 如图: 举个例子 (字符串 "abcabcdef" 匹配字符串 "abcdef"): 次数暴力匹配 KMP 算法说明 1 abcabcdef abcdef
Java 数据结构与算法系列精讲之单向链表

目录概述链表单向链表单向链表实现 Node类 add方法 remove方法 get方法 set方法 contain方法 main 完整代码概述从今天开始, 小白我将带大家开启 Jave 数据结构 & 算法的新篇章. 链表链表 (Linked List) 是一种递归的动态数据结构. 链表以线性表的形式, 在每一个节点存放下一个节点的指针. 链表解决了数组需要先知道数据大小的缺点, 增加了节点的指针域, 空间开销较大. 链表包括三类: 单向链表双向链表循环链表单向链表单向链表
Java 数据结构与算法系列精讲之环形链表

目录概述链表环形链表环形链表实现 Node类 insert方法 remove方法 main 完整代码概述从今天开始, 小白我将带大家开启 Java 数据结构 & 算法的新篇章. 链表链表 (Linked List) 是一种递归的动态数据结构. 链表以线性表的形式, 在每一个节点存放下一个节点的指针. 链表解决了数组需要先知道数据大小的缺点, 增加了节点的指针域, 空间开销较大. 链表包括三类: 单向链表双向链表循环链表环形链表环形链表 (Circular Linked Li
Java 数据结构与算法系列精讲之栈

目录概述栈栈实现 push方法 pop方法 main 完整代码概述从今天开始, 小白我将带大家开启 Jave 数据结构 & 算法的新篇章. 栈栈 (Stack) 是一种运算受限的线性表, 遵循先进后出的原则 (Last-In-First-Out). 举个例子, 当我们灌调料的时候, 后灌进去的调料会先被使用. 栈只能在表尾部进行插入和删除的操作. 开口的一端被称为栈顶, 另一端则被称为栈底. 如图: 栈实现 push 方法栈 (Stack) 的 push 方法, 把项压入栈顶部.
Java 数据结构与算法系列精讲之数组

目录概述数组声明数组的两个方法创建数组的两个方法索引自定义数组泛型构造函数元素操作调用完整代码概述从今天开始, 小白我将带大家开启 Jave 数据结构 & 算法的新篇章. 数组数组 (Array) 是有序数据的集合, 在 Java 中 java.util.Arrays包含用来操作数组的各种方法, 比如排序和搜索等. 其所有方法均为静态方法, 调用起来非常简单. 声明数组的两个方法方法一: 数据类型[] array; 方法二: 数据类型 array[]; 创建数组的两
Java 数据结构与算法系列精讲之二叉堆

目录概述优先队列二叉堆二叉堆实现获取索引添加元素 siftUp 完整代码概述从今天开始, 小白我将带大家开启 Java 数据结构 & 算法的新篇章. 优先队列优先队列 (Priority Queue) 和队列一样, 是一种先进先出的数据结构. 优先队列中的每个元素有各自的优先级, 优先级最高的元素最先得到服务. 如图: 二叉堆二叉堆 (Binary Heap) 是一种特殊的堆, 二叉堆具有堆的性质和二叉树的性质. 二叉堆中的任意一节点的值总是大于等于其孩子节点值. 如图: 二
Java 数据结构与算法系列精讲之时间复杂度与空间复杂度

目录概述算法的衡量标准时间复杂度最优时间复杂度平均时间复杂度最坏时间复杂度 O(1) O(n) O(n^2) O(logN) 空间复杂度 O(1) O(n) 概述从今天开始, 小白我将带大家开启 Jave 数据结构 & 算法的新篇章. 算法的衡量标准当我们需要衡量一个算法的的优越性, 通常会使用时间复杂度 (Time Complexity) 和空间复杂度 (Space Complexity) 来衡量. 时间复杂度时间复杂度 (Time Complexity) 通常用 O(n)

Java 数据结构与算法系列精讲之KMP算法

概述

KMP 算法

部分匹配表

KMP 算法实现

相关推荐

随机推荐