Java数据结构之优先级队列(堆)图文详解

目录

• 一、堆的概念
• 二、向下调整
• 1.建初堆
• 2.建堆
• 三、优先级队列
• 1.什么是优先队列？
• 2.入队列
• 3.出队列
• 4.返回队首元素
• 5.堆的其他TopK问题
• 总结：
• 总结

一、堆的概念

堆的定义：n个元素的序列{k1 , k2 , … , kn}称之为堆，当且仅当满足以下条件时：

（1）ki >= k2i 且 ki >= k(2i+1) ——大根堆

（2） ki <= k2i 且 ki <= k(2i+1) ——小根堆

简单来说：

堆是具有以下性质的完全二叉树：
（1）每个结点的值都大于或等于其左右孩子结点的值，称为大根堆（如左下图）；
或者：
（1）每个结点的值都小于或等于其左右孩子结点的值，称为小根堆（如右下图）。

我们使用数组保存二叉树结构，即是将二叉树用层序遍历方式放入数组中，如上图。

堆的元素下标存在以下关系：

1.假如已知双亲（parent）的下标，则

左孩子（left）下标 = 2parent + 1；

右孩子（right）下标 = 2parent +2；

2.已知孩子（child）（不区分左右）下标，则：

双亲（parent）下标 = （child - 1）/ 2 ;

小结：

• 堆逻辑上是一棵完全二叉树；
• 堆物理上保存在数组中；
• 满足任意结点的值都大于其子树中结点的值，叫做大堆，或者大根堆，或者最大堆；反之，则是小堆，或者小根堆，或者最小堆；
• 堆的基本作用是，快速找集合中的最值。

二、向下调整

1.建初堆

设有一个无序序列 {2,5,7,8,4,6,3,0,9,1 }，下面通过图解来建初始堆。

这里有一个前提：这棵二叉树的左右子树都必须是一个堆，才能进行调整。

下面是用到的数据的一些说明：

• array 代表存储堆的数组
• size 代表数组中被视为堆数据的个数
• index 代表要调整位置的下标
• left 代表 index 左孩子下标
• right 代表 index 右孩子下标
• min 代表 index 的最小值孩子的下标

过程文字描述如下：

1.index 如果已经是叶子结点，则整个调整过程结束：

（1）判断 index 位置有没有孩子；

（2） 因为堆是完全二叉树，没有左孩子就一定没有右孩子，所以判断是否有左孩子；

（3） 因为堆的存储结构是数组，所以判断是否有左孩子即判断左孩子下标是否越界，即 left >= size 越界。

2.确定 left 或 right，谁是 index 的最小孩子 min：

（1） 如果右孩子不存在，则 min = left；

（2）否则，比较 array[left] 和 array[right] 值得大小，选择小的为 min；

（3）比较 array[index] 的值 和 array[min] 的值，如果 array[index] <= array[min]，则满足堆的性质，调整结束。

3.否则，交换 array[index] 和 array[min] 的值；

4.然后因为 min 位置的堆的性质可能被破坏，所以把 min 视作 index，向下重复以上过程。

通过上面的操作描述，我们写出以下代码：

public static void shiftDown(int[] array, int size, int index){
        int left = 2*index +1;
        while(left < size){
            int min = left;
            int right = 2*index +2;
            if(right<size){
                if(array[right] < array[left]){
                    min = right;
                }
            }
            if(array[index] <= array[min]){
                break;
            }
            int tmp = array[index];
            array[index] = array[min];
            array[min] = tmp;
            index = min;
            left = 2*index +1;
        }
    }

时间复杂度为 O(log(n))。

2.建堆

下面我们给出一个数组，这个数组逻辑上可以看做一颗完全二叉树，但是还不是一个堆，现在我们通过算法，把它构建成一个堆。根节点左右子树不是堆，我们怎么调整呢？这里我们从倒数的第一个非叶子节点的子树开始调整，一直调整到根节点的树，就可以调整成堆。

时间复杂度分析：

粗略估算，可以认为是在循环中执行向下调整，为 O(n * log(n))，（了解）实际上是 O(n)。

//建堆代码
    public void createHeap(int[] array) {
        for (int i = 0; i < array.length; i++) {
            elem[i] = array[i];
            usedSize++;
        }
        //根据代码 显示的时间复杂度   看起来 应该是O(n*logn)  但是 实际上是O(n)
        for (int parent = (usedSize-1-1)/2; parent >= 0 ; parent--) {
            //调整
            shiftDown(parent,usedSize);
        }
    }

三、优先级队列

1.什么是优先队列？

根据百科解释：

普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出（first in, largest out）的行为特征。通常采用堆数据结构来实现。

所以我们在这里实现优先队列的内部原理是堆，也就是说采用堆来构建。

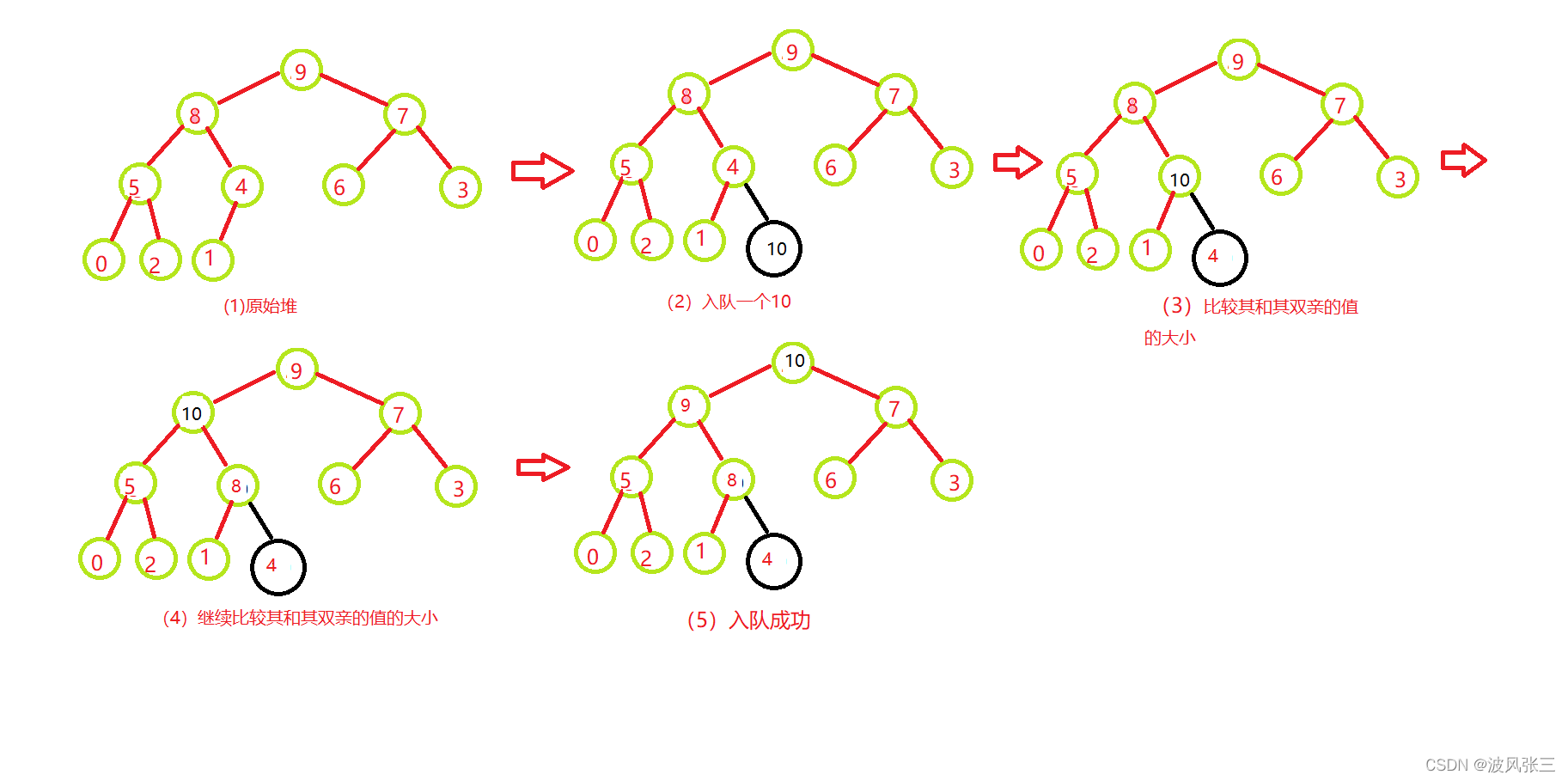
2.入队列

过程（以大堆为例）：

• 首先按尾插方式放入数组；
• 比较其和其双亲的值的大小，如果双亲的值大，则满足堆的性质，插入结束；
• 否则，交换其和双亲位置的值，重新进行 2、3 步骤；
• 直到根结点。

下面图解：

    private void shiftUp(int child) {
        int parent = (child-1)/2;
        while (child > 0) {
            if(elem[child] > elem[parent]) {
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                child = parent;
                parent = (child-1)/2;
            }else {
                break;
            }
        }
    }

3.出队列

为了防止破坏堆的结构，删除时并不是直接将堆顶元素删除，而是用数组的最后一个元素替换堆顶元素，然后通过向 下调整方式重新调整成堆。

    private void shiftUp(int child) {
        int parent = (child-1)/2;
        while (child > 0) {
            if(elem[child] > elem[parent]) {
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                child = parent;
                parent = (child-1)/2;
            }else {
                break;
            }
        }
    }

    public void offer(int val) {
        if(isFull()) {
            //扩容
            elem = Arrays.copyOf(elem,2*elem.length);
        }
        elem[usedSize++] = val;
        //注意这里传入的是usedSize-1
        shiftUp(usedSize-1);
    }

4.返回队首元素

直接返回堆顶元素

    public int peek() {
        if(isEmpty()) {
            throw new RuntimeException("优先级队列为空！");
        }
        return elem[0];
    }

    public boolean isEmpty() {
        return usedSize == 0;
    }

整体的代码：

public class TestHeap {
    public int[] elem;
    public int usedSize;

    public TestHeap() {
        this.elem = new int[10];
    }

    /**
     * 向下调整函数的实现
     * @param parent 每棵树的根节点
     * @param len 每棵树的调整的结束位置  10
     */
    public void shiftDown(int parent,int len) {
        int child = 2*parent+1;
        //1、最起码 是有左孩子的，至少有1个孩子
        while (child < len) {
            if(child+1 < len && elem[child] < elem[child+1]) {
                child++;//保证当前左右孩子最大值的下标
            }
            if(elem[child] > elem[parent]) {
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                parent = child;
                child = 2*parent+1;
            }else {
                break;
            }
        }
    }

    public void createHeap(int[] array) {
        for (int i = 0; i < array.length; i++) {
            elem[i] = array[i];
            usedSize++;
        }
        //根据代码 显示的时间复杂度   看起来 应该是O(n*logn)  但是 实际上是O(n)
        for (int parent = (usedSize-1-1)/2; parent >= 0 ; parent--) {
            //调整
            shiftDown(parent,usedSize);
        }
    }

    private void shiftUp(int child) {
        int parent = (child-1)/2;
        while (child > 0) {
            if(elem[child] > elem[parent]) {
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                child = parent;
                parent = (child-1)/2;
            }else {
                break;
            }
        }
    }

    public void offer(int val) {
        if(isFull()) {
            //扩容
            elem = Arrays.copyOf(elem,2*elem.length);
        }
        elem[usedSize++] = val;
        //注意这里传入的是usedSize-1
        shiftUp(usedSize-1);
    }

    public boolean isFull() {
        return usedSize == elem.length;
    }

    public int poll() {
        if(isEmpty()) {
            throw new RuntimeException("优先级队列为空！");
        }
        int tmp = elem[0];
        elem[0] = elem[usedSize-1];
        elem[usedSize-1] = tmp;
        usedSize--;
        shiftDown(0,usedSize);
        return tmp;
    }

    public int peek() {
        if(isEmpty()) {
            throw new RuntimeException("优先级队列为空！");
        }
        return elem[0];
    }

    public boolean isEmpty() {
        return usedSize == 0;
    }

    public void heapSort() {
        int end = this.usedSize-1;
        while (end > 0) {
            int tmp = elem[0];
            elem[0] = elem[end];
            elem[end] = tmp;
            shiftDown(0,end);
            end--;
        }
    }

}

5.堆的其他TopK问题

什么是TopK问题？

从arr[1, n]这n个数中，找出最大的k个数，这就是经典的TopK问题。

解决这类问题，我们往往会有以下几种思路：

• 对整体进行排序，输出前10个最大的元素。
• 用上面刚刚讲的堆。
• 也是用堆，不过这比第二个思路更巧妙。

我们直接讲思路三：

1. 先用前k个元素生成一个小顶堆，这个小顶堆用于存储，当前最大的k个元素。
2. 接着，从第k+1个元素开始扫描，和堆顶（堆中最小的元素）比较，如果被扫描的元素大于堆顶，则替换堆顶的元素，并调整堆，以保证堆内的k个元素，总是当前最大的k个元素。
3. 直到，扫描完所有n-k个元素，最终堆中的k个元素，就是所要求的TopK。

以这个数组{12，15，21，41，30}为例，找到前3个最大的元素。

那如果是将一组进行从小到大排序，我们该采用大根堆还是小根堆？

答案是：大根堆！

步骤如下：

• 将这组数据调整为大根堆调整为大根堆；
• 0下标和最后1个未排序的元素进行交换即可；
• 重复1、2，直到结束。

总结：

如果求前K个最大的元素，要建一个小根堆。如果求前K个最小的元素，要建一个大根堆。第K大的元素。建一个小堆，堆顶元素就是第K大的元素。第K小的元素。建一个大堆，堆顶元素就是第K小的元素。

    public void heapSort() {
        int end = this.usedSize-1;
        while (end > 0) {
            int tmp = elem[0];
            elem[0] = elem[end];
            elem[end] = tmp;
            shiftDown(0,end);
            end--;
        }
    }
    public void shiftDown(int parent,int len) {
        int child = 2*parent+1;
        //1、最起码 是有左孩子的，至少有1个孩子
        while (child < len) {
            if(child+1 < len && elem[child] < elem[child+1]) {
                child++;//保证当前左右孩子最大值的下标
            }
            if(elem[child] > elem[parent]) {
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                parent = child;
                child = 2*parent+1;
            }else {
                break;
            }
        }
    }

总结

来来回回，这篇文章写了2-3天了，以前写文章总是蜻蜓点水，不到水深，导致自己对很多的知识也没有多深理解，仅仅是为了写文章而写文章。希望有改变，从这篇文章开始吧！

到此这篇关于Java数据结构之优先级队列(堆)的文章就介绍到这了,更多相关Java优先级队列(堆)内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！