C语言每日练习之二叉堆

目录

• 一、堆的概念
• 1、概述
• 2、定义
• 3、性质
• 4、作用
• 二、堆的存储结构
• 1、根结点编号
• 2、孩子结点编号
• 3、父结点编号
• 4、数据域
• 5、堆的数据结构
• 三、堆的常用接口
• 1、元素比较
• 2、交换元素
• 3、空判定
• 4、满判定
• 5、上浮操作
• 6、下沉操作
• 四、堆的创建
• 1、算法描述
• 2、动画演示
• 3、源码详解
• 五、堆元素的插入
• 1、算法描述
• 2、动画演示
• 3、源码详解
• 五、堆元素的删除
• 1、算法描述
• 2、动画演示
• 3、源码详解
• 总结

一、堆的概念

1、概述

堆是计算机科学中一类特殊的数据结构的统称。实现有很多，例如：大顶堆，小顶堆，斐波那契堆，左偏堆，斜堆 等等。从子结点个数上可以分为二叉堆，N叉堆等等。本文将介绍的是 二叉堆。

2、定义

二叉堆本质是一棵完全二叉树，所以每次元素的插入删除都能保证 O ( l o g 2 n ) O(log_2n) O(log2​n)。根据堆的偏序规则，分为 小顶堆 和 大顶堆。小顶堆，顾名思义，根结点的关键字最小；大顶堆则相反。如图所示，表示的是一个大顶堆。

3、性质

以大顶堆为例，它总是满足下列性质：
1）空树是一个大顶堆；

2）大顶堆中某个结点的关键字 小于等于 其父结点的关键字；

3）大顶堆是一棵完全二叉树。有关完全二叉树的内容，可以参考：画解完全二叉树。

如下图所示，任意一个从叶子结点到根结点的路径总是一个单调不降的序列。

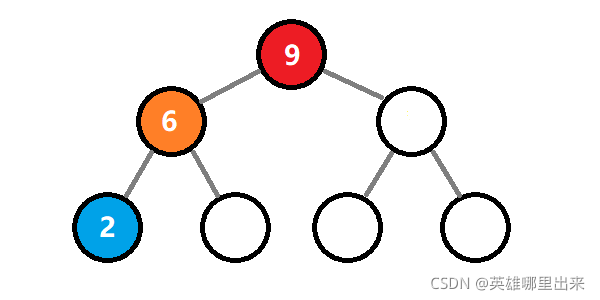
小顶堆只要把上文中的 小于等于 替换成 大于等于 即可。

4、作用

还是以大顶堆为例，堆能够在 O ( 1 ) O(1) O(1) 的时间内，获得 关键字 最大的元素。并且能够在 O ( l o g 2 n ) O(log_2n) O(log2​n) 的时间内执行插入和删除。一般用来做 优先队列 的实现。

二、堆的存储结构

学习堆的过程中，我们能够学到一种新的表示形式。就是：利用 数组 来表示 链式结构。怎么理解这句话呢？

由于堆本身是一棵完全二叉树，所以我们可以把每个结点，按照层序映射到一个顺序存储的数组中，然后利用每个结点在数组中的下标，来确定结点之间的关系。

如图所示，描述的是堆结点下标和结点之间的关系，结点上的数字代表的是 数组下标。从左往右按照层序进行连续递增。

1、根结点编号

根结点的编号，看作者的喜好。可以用 0 或者 1。本文的作者是 C语言 出身，所以更倾向于选择 0 作为根结点的编号（因为用 1 作为根结点编号的话，数组的第 0 个元素就浪费了）。

我们可以用一个宏定义来实现它的定义，如下：

#define root 0

2、孩子结点编号

那么，根结点的两个左右子树的编号，就分别为 1 和 2 了。以此类推，按照层序进行编号的话，1 的左右子树编号为 3 和 4；2 的左右子树编号为 5 和 6。

根据数学归纳法，对于编号为 i i i 的结点，它的左子树编号为 2 i + 1 2i+1 2i+1，右子树编号为 2 i + 2 2i+2 2i+2。用宏定义实现如下：

#define lson(idx) (2*idx+1)
#define rson(idx) (2*idx+2)

由于这里涉及到乘 2，所以我们还可以用左移位运算来优化乘法运算，如下：

#define lson(idx) (idx << 1|1)
#define rson(idx) ((idx + 1) << 1)

3、父结点编号

同样，父结点编号也可以通过数学归纳法得出，当结点编号为 i i i 时，它的父结点编号为 i − 1 2 \frac {i-1} {2} 2i−1​，利用C语言实现如下：

#define parent(idx) ((idx - 1) / 2)

这里涉及到除 2，可以利用右移运算符进行优化，如下：

#define parent(idx) ((idx - 1) >> 1)

这里利用补码的性质，根结点的父结点得到的值为 -1；

4、数据域

堆数据元素的数据域可以定义两个：关键字 和 值，其中关键字一般是整数，方便进行比较确定大小关系；值则是用于展示用，可以是任意类型，可以用typedef struct进行定义如下：

typedef struct {
    int key;      // (1)
    void *any;    // (2)
}DataType;

• (1) 关键字；
• (2) 值，定义成一个空指针，可以用来表示任意类型；

5、堆的数据结构

由于堆本质上是一棵完全二叉树，所以将它一一映射到数组后，一定是连续的。我们可以用一个数组来代表一个堆，在C语言中的数组拥有一个固定长度，可以用一个Heap结构体表示如下：

typedef struct {
    DataType *data;  // (1)
    int size;        // (2)
    int capacity;    // (3)
}Heap;

• (1) 堆元素所在数组的首地址；
• (2) 堆元素个数；
• (3) 堆的最大元素个数；

三、堆的常用接口

1、元素比较

两个堆元素的比较可以采用一个比较函数compareData来完成，比较过程就是对关键字key进行比较的过程，以大顶堆为例：

a. 大于返回 -1，代表需要执行交换；

b. 小于返回 1，代表需要执行交换；

c. 等于返回 0，代表需要执行交换；

int compareData(const DataType* a, const DataType* b) {
    if(a->key > b->key) {
        return -1;
    }else if(a->key < b->key) {
        return 1;
    }
    return 0;
}

2、交换元素

交换两个元素的位置，也是堆这种数据结构中很常见的操作，C语言实现也比较简单，如下：

void swap(DataType* a, DataType* b) {
    DataType tmp = *a;
    *a = *b;
    *b = tmp;
}

3、空判定

空判定是一个查询接口，即询问堆是否是空的，实现如下：

bool HeapIsEmpty(Heap *heap) {
    return heap->size == 0;
}

4、满判定

满判定是一个查询接口，即询问堆是否是满的，实现如下：

bool heapIsFull(Heap *heap) {
    return heap->size == heap->capacity;
}

5、上浮操作

对于大顶堆而言，从它叶子结点到根结点的元素关键字一定是单调不降的，如果某个元素出现了比它的父结点大的情况，就需要进行上浮操作。

上浮操作就是对 当前结点 和 父结点 进行比较，如果它的关键字比父结点大（compareData返回-1的情况），将它和父结点进行交换，继续上浮操作；否则，终止上浮操作。

如图所示，代表的是一个关键字为 95 的结点，通过不断上浮，到达根结点的过程。上浮完毕以后，它还是一个大顶堆。

上浮过程的 C语言 实现如下：

void heapShiftUp(Heap* heap, int curr) {               // (1)
    int par = parent(curr);                            // (2)
    while(par >= root) {                               // (3)
        if( compareData( &heap->data[curr], &heap->data[par] ) < 0 ) {
            swap(&heap->data[curr], &heap->data[par]); // (4)
            curr = par;
            par = parent(curr);
        }else {
            break;                                     // (5)
        }
    }
}

(1) heapShiftUp这个接口是一个内部接口，所以用小写驼峰区分，用于实现对堆中元素进行插入的时候的上浮操作；

(2) curr表示需要进行上浮操作的结点在堆中的编号，par表示curr的父结点编号；

(3) 如果已经是根结点，则无须进行上浮操作；

(4) 子结点的关键字 大于 父结点的关键字，则执行交换，并且更新新的 当前结点 和 父结点编号；

(5) 否则，说明已经正确归位，上浮操作结束，跳出循环；

6、下沉操作

对于大顶堆而言，从它 根结点 到 叶子结点 的元素关键字一定是单调不增的，如果某个元素出现了比它的某个子结点小的情况，就需要进行下沉操作。

下沉操作就是对 当前结点 和 关键字相对较小的子结点 进行比较，如果它的关键字比子结点小，将它和这个子结点进行交换，继续下沉操作；否则，终止下沉操作。

如图所示，代表的是一个关键字为 19 的结点，通过不断下沉，到达叶子结点的过程。下沉完毕以后，它还是一个大顶堆。

下沉过程的 C语言 实现如下：

void heapShiftDown(Heap* heap, int curr) {            // (1)    int son = lson(curr);                             // (2)    while(son < heap->size) {        if( rson(curr) < heap->size ) {            if( compareData( &heap->data[rson(curr)], &heap->data[son] ) < 0 ) {                son = rson(curr);                     // (3)             }                }        if( compareData( &heap->data[son], &heap->data[curr] ) < 0 ) {            swap(&heap->data[son], &heap->data[curr]); // (4)            curr = son;            son = lson(curr);        }else {            break;                                     // (5)         }    }}void heapShiftDown(Heap* heap, int curr) {            // (1)
    int son = lson(curr);                             // (2)
    while(son < heap->size) {
        if( rson(curr) < heap->size ) {
            if( compareData( &heap->data[rson(curr)], &heap->data[son] ) < 0 ) {
                son = rson(curr);                     // (3)
            }
        }
        if( compareData( &heap->data[son], &heap->data[curr] ) < 0 ) {
            swap(&heap->data[son], &heap->data[curr]); // (4)
            curr = son;
            son = lson(curr);
        }else {
            break;                                     // (5)
        }
    }
}

(1) heapShiftDown这个接口是一个内部接口，所以用小写驼峰区分，用于对堆中元素进行删除的时候的下沉调整；

(2) curr表示需要进行下沉操作的结点在堆中的编号，son表示curr的左儿子结点编号；

(3) 始终选择关键字更小的子结点；

(4) 子结点的值小于父结点，则执行交换；

(5) 否则，说明已经正确归位，下沉操作结束，跳出循环；

四、堆的创建

1、算法描述

通过给定的数据集合，创建堆。可以先创建堆数组的内存空间，然后一个一个执行堆的插入操作。插入操作的具体实现，会在下文继续讲解。

2、动画演示

3、源码详解

Heap* HeapCreate(DataType *data, int dataSize, int maxSize) {    // (1)
    int i;
    Heap *h = (Heap *)malloc( sizeof(Heap) );                    // (2)
    h->data = (DataType *)malloc( sizeof(DataType) * maxSize );  // (3)
    h->size = 0;                                                 // (4)
    h->capacity = maxSize;                                       // (5)
    for(i = 0; i < dataSize; ++i) {
        HeapPush(h, data[i]);                                    // (6)
    }
    return h;                                                    // (7)
}

(1) 给定一个元素个数为dataSize的数组data，创建一个最大元素个数为maxSize的堆并返回堆的结构体指针；

(2) 利用malloc申请堆的结构体的内存；

(3) 利用malloc申请存储堆数据的数组的内存空间；

(4) 初始化空堆；

(5) 初始化堆最大元素个数为maxSize；

(6) 遍历数组执行堆的插入操作，插入的具体实现HeapPush接下来会讲到；

(7) 最后，返回堆的结构体指针；

五、堆元素的插入

1、算法描述

堆元素的插入过程，就是先将元素插入堆数组的最后一个位置，然后执行上浮操作；

2、动画演示

3、源码详解

bool HeapPop(Heap *heap) {
    if(HeapIsEmpty(heap)) {
        return false;                               // (1)
    }
    heap->data[root] = heap->data[ --heap->size ];  // (2)
    heapShiftDown(heap, root);                      // (3)
    return true;
}

(1) 堆已满，不能进行插入；

(2) 插入堆数组的最后一个位置；

(3) 对最后一个位置的 堆元素 执行上浮操作；

五、堆元素的删除

1、算法描述

堆元素的删除，只能对堆顶元素进行操作，可以将数组的最后一个元素放到堆顶，然后对堆顶元素进行下沉操作。

2、动画演示

3、源码详解

bool HeapPop(Heap *heap) {
    if(HeapIsEmpty(heap)) {
        return false;                               // (1)
    }
    heap->data[root] = heap->data[ --heap->size ];  // (2)
    heapShiftDown(heap, root);                      // (3)
    return true;
}

• (1) 堆已空，无法执行删除；
• (2) 将堆数组的最后一个元素放入堆顶，相当于删除了堆顶元素；
• (3) 对堆顶元素执行下沉操作；

总结

本篇文章就到这里了，希望能够给你带来帮助，也希望您能够多多关注我们的更多内容!