Python数据分析应用之Matplotlib数据可视化详情

目录

• 简述
• 掌握绘图基础语法与基本参数 掌握pyplot基础语法
• pyplot中的基础绘图语法
• 包含子图的基础语法
• 调节线条的rc参数
• 调节字体的rc参数
• 分析特征间的关系
• 绘制散点图
• 绘制2000-2017年个季度过敏生产总值散点图
• 绘制2000-2017年各季度国民生产总值散点图
• 绘制折线图
• 绘制2000-2017年各季度过敏生产总值折线图
• 2000~ 2017年各季度国民生产总值点线图
• 2000~ 2017年各季度国民生产总值折线散点图
• 任务实现
• 任务1
• 任务2
• 分析特征内部数据分布与分散状况
• 绘制饼图
• 绘制箱线图
• 任务实现
• 实训

简述

mat参照了函数设计，plot表示绘图的作用，lib则表示一个集合。今年在开源社区的推动下，Matplotlib在科学计算领域得到了广泛的应用，成为Python中应用非常广的绘图工具之一。其中Matplotlib应用最广的是matplotlib.pyplot模块。

matplotlib.pyplot是一个命令风格函数的集合，使得Matplotlib的机制更像MATLAB。每个绘图函数都可对图形进行一些修改，如创建图形，在图形中创建绘图区域，在绘图区域绘制一些线条，使用标签装饰绘图等。在pyplot中，各种状态跨函数调用保存，以便跟踪诸如当前图形和绘图 区域之类的东西，并且绘图函数始终指向当前轴域。本章以pyplot为基础介绍和展开学习。

学习目标 ：

• 掌握pyplot常用的绘图参数的调节方法掌
• 握子图的绘制方法
• 掌握绘制图形的保存与展示方法
• 掌握散点图和折线图的作用与绘制方法
• 掌握直方图、饼图和箱线图的作用与绘制方法

掌握绘图基础语法与基本参数 掌握pyplot基础语法

大部分的pyplot图形绘制都遵循一个流程，使用这个流程可以完成大部分图形的绘制。pyplot基本绘图流程主要分为3个部分。

创建画布与创建子图：

构建出一张空白的画布，并可以选择是否将整个画布划分为多个部分，方便在同一幅图上绘制多个图形的情况。当只需要绘制一幅简单的图形时，就可以不用分割。
pyplot创建画布与选中子图的常用函数

添加画布内容：

第二部分是绘图的主体。
包括添加标题、添加坐标名称、绘制图形等步骤是并列的，没有先后。但添加图例一定是在绘制图形之后进行的。
pyplot中添加各类标签和图例的常用函数

保存与显示图形：

第三部分用于保存和显示图形，通常只有两个函数，参数也很少
pyplot中保存额和显示图形的常用函数

pyplot中的基础绘图语法

import numpy as np
import matplotlib.pyplot as plt
#matplotlib inline表示在行中显示图片，在命令行运行报错
data=np.arange(0110.01)
plt.title('lines')# 添加标题
plt.xlabel('x')#添加x轴的名称
plt.ylabel('y')#添加y轴的名称
plt.xlim((0,1))#确定x轴范围
plt.ylim((0,1))#确定y轴范围
plt.xticks([0,0.2,0.4,0.6,0.8,1])#规定x轴刻度
plt.yticks([0,0.2,0.4,0.6,0.8,1])#确定y轴刻度
plt.plot(data,data**2)#添加y=x^2曲线
plt.plot(data,data**4)#添加y=x^4曲线
plt.legend(['y=x^2','y=x^4'])
plt.savefig(' 3-1.png')
plt.show()

包含子图的基础语法

import numpy as np
import matplotlib.pyplot as plt

rad = np.arange(0, np.pi * 2, 0.01)
# 第一幅子图
p1 = plt.figure(figsize=(8, 6), dpi=80)  # 确定画布大小
ax1 = p1.add_subplot(2, 1, 1)  # 创建一个2行1列的子图
plt.title('lines')  # 添加标题
plt.xlabel('x')  # 添加x轴的名称
plt.ylabel('y')  # 添加y轴的名称
plt.xlim((0, 1))  # 确定x轴范围
plt.ylim((0, 1))  # 确定y轴范围
plt.xticks([0, 0.2, 0.4, 0.6, 0.8, 1])  # 确定x轴刻度
plt.yticks([0, 0.2, 0.4, 0.6, 0.8, 1])  # 确定y轴刻度
plt.plot(rad, rad ** 2)  # 添加曲线
plt.plot(rad, rad ** 4)  # 添加曲线
plt.legend(['y=x^2'], ['y=x^4'])
# 第二幅子图
ax2 = p1.add_subplot(2, 1, 2)  # 开始绘制第二幅
plt.title('sin/cos')
plt.xlabel('rad')
plt.ylabel('value')
plt.xlim((0, np.pi * 2))
plt.ylim((-1, 1))
plt.xticks([0, np.pi / 2, np.pi, np.pi * 1.5, np.pi * 2])
plt.yticks([-1, -0.5, 0, 0.5, 1])
plt.plot(rad, np.sin(rad))
plt.plot(rad, np.cos(rad))
plt.legend(['sin'], ['cos'])
plt.savefig('sincos.png')
plt.show()

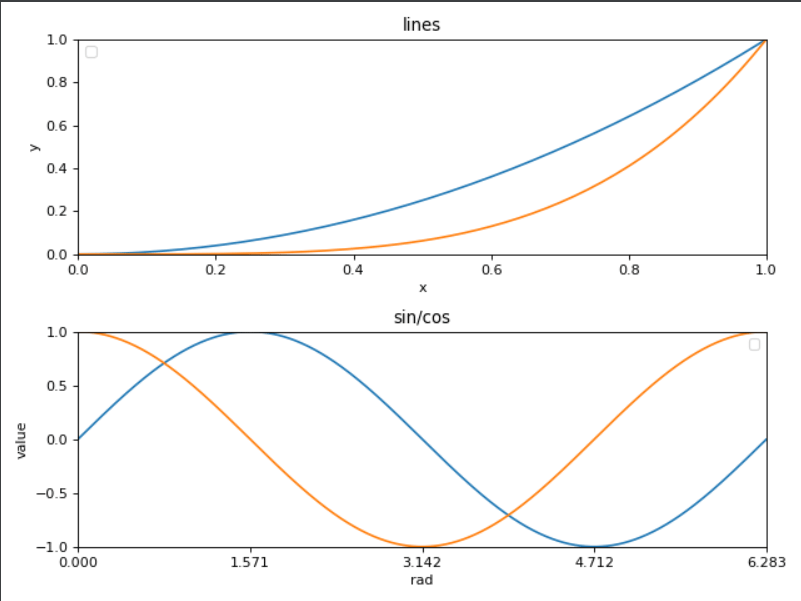
设置pyplot的动态rc参数：

pyplot使用rc配置文件来自定义图形的各种默认属性，被称为rc配置或rc参数。

默认rc参数可以在python交互式环境中动态更改。所有存储在字变量中的rc参数被称为rcParams。rc参数在修改过后，绘图时使用默认的参数就会改变。

调节线条的rc参数

import numpy as np
import matplotlib.pyplot as plt

# 原图
x = np.linspace(0, 4 * np.pi)
y = np.sin(x)
plt.plot(x, y, label="$sin(x)$")
plt.title('sin')
plt.savefig('默认sin曲线.png')
plt.show()

import numpy as np
import matplotlib.pyplot as plt

#修改RC参数后的图
plt.rcParams['lines.linestyle'] = '-.'
plt.rcParams['lines.linewidth']=3
plt.plot(x,y,label="$sin(x)$")
plt.title('sin')
plt.savefig('修改rc参数后sin曲线.png')
plt.show()

线条常用的rc参数名称。解释与取值：

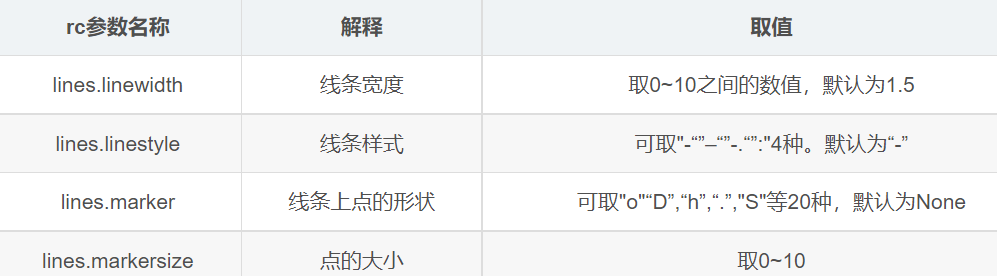
lines.linstyle参数取值及其含义：

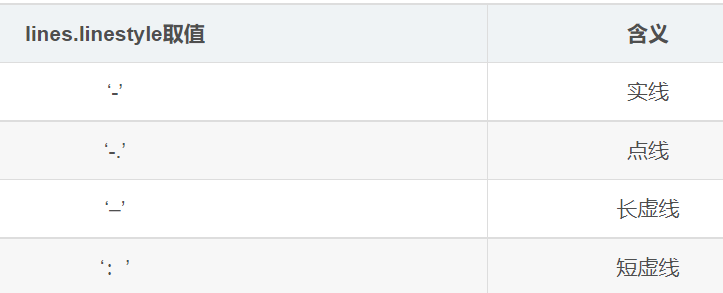
lines.marker参数取值及其意义：

lines.marker取值含义o圆圈D菱形h六边形1H六边形2-水平线8八边形P五边形，像素+加号None无、点s正方形*星号d小菱形v一角朝下的三角形<一角朝左的三角形>一角朝右的三角形^一角朝上的三角形|竖线xX

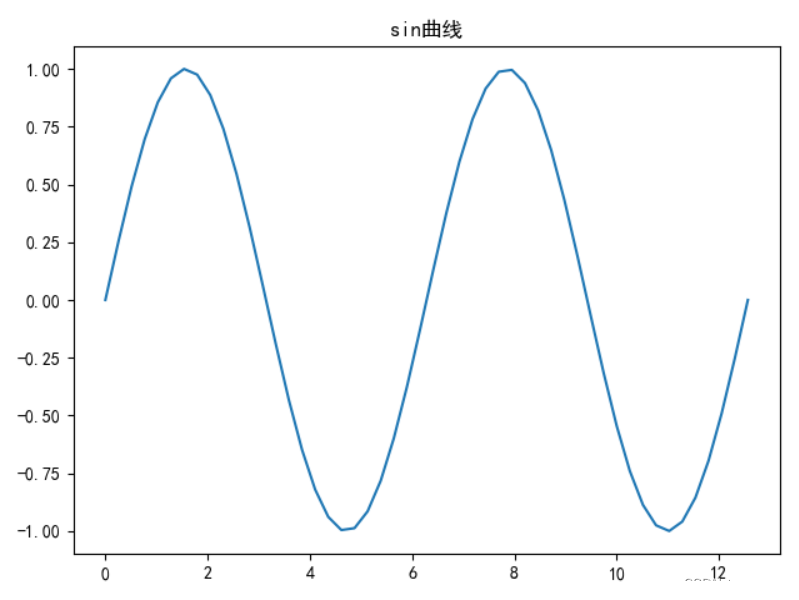
调节字体的rc参数

import numpy as np
import matplotlib.pyplot as plt

# 无法显示中文标题
x = np.linspace(0, 4 * np.pi)
y = np.sin(x)
plt.plot(x, y, label="$sin(x)$")
plt.title('sin曲线')
plt.savefig('无法显示中文标题sin曲线.png')
plt.show()

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'  # 汉字字体,优先使用楷体，如果找不到楷体，则使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 这两行需要手动设置

# 修改rc参数后的图
plt.plot(x, y, label='$sin(x)$')
plt.title('sin')
plt.savefig('修改rc参数后的sin曲线.png')
plt.show()

分析特征间的关系

绘制散点图

散点图，是利用坐标即散点的分布形态反映特征间的统计关系的一种图形。值由点在图表中的位置表示，类别由图中的不同标记表示，通常用于比较跨类别的数据。

散点图可以提供两类关键信息：

• 特征之间是否存在数值或者数量的关联趋势，关联趋势是线性的还是非线性的
• 如果某个点或者几个点偏离大多数点，这个点就是离群值，通过散点图可以一目了然，从而可以进一步分析这些离群值是否存在建模分析中产生很大的影响。

scatter函数常用参数及说明：

绘制2000-2017年个季度过敏生产总值散点图

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False

data = np.load('35data.npz/国民经济核算季度数据.npz', allow_pickle=True)
name = data['columns']
values = data['values']
plt.figure(figsize=(8, 7))
plt.scatter(values[:, 0], values[:, 2], marker='o')
plt.xlabel('年份')
plt.ylabel('生产总值(亿元)')
plt.ylim((0, 225000))
plt.xticks(range(0, 70, 4), values[range(0, 70, 4), 1], rotation=45)
plt.title('绘制2000-2017年个季度过敏生产总值散点图')
plt.savefig('绘制2000-2017年个季度过敏生产总值散点图.png')
plt.show()

绘制2000-2017年各季度国民生产总值散点图

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'  # 汉字字体,优先使用楷体，如果找不到楷体，则使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 这两行需要手动设置

plt.figure(figsize=(8, 7))
data = np.load('35data.npz/国民经济核算季度数据.npz', allow_pickle=True)
values = data['values']
# 绘制散点图1
plt.scatter(values[:, 0], values[:, 3], marker='o', c='red')
# 绘制散点图2
plt.scatter(values[:, 0], values[:, 4], marker='D', c='blue')
# 绘制散点图3
plt.scatter(values[:, 0], values[:, 5], marker='v', c='yellow')
plt.xlabel('年份')
plt.ylabel('生产总值（亿元）')
plt.xticks(range(0, 70, 4), values[range(0, 70, 4), 1], rotation=45)
plt.title('2000-2017年各季度国民生产总值散点图')
plt.legend(['第一产业', '第二产业', '第三产业'])
plt.savefig('2000-2017年各季度国民生产总值散点图.png')
plt.show()

绘制折线图

折线图：将数据点按照顺序连接起来的图形。适合用于显示随时间而变化的连续数据。同时还可以看出数量的差异，增长趋势的变化。

pyplot绘制折线图的函数为plot，基本语法如下：
matplotlib.pyplot.plot(*args,**kwargs)

绘制2000-2017年各季度过敏生产总值折线图

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'  # 汉字字体,优先使用楷体，如果找不到楷体，则使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 这两行需要手动设置

plt.figure(figsize=(8, 7))
#,
data = np.load('35data.npz/国民经济核算季度数据.npz',allow_pickle=True)
values = data['values']
plt.plot(values[:, 0], values[:, 2], color='r', linestyle='--')
plt.xlabel('年份')
plt.ylabel('生产总值（亿元）')
plt.ylim((0, 225000))
plt.xticks(range(0, 70, 4), values[range(0, 70, 4), 1], rotation=45)
plt.title('2000~ 2017 年各季度 国民生产 总值折线')
plt.savefig('2000~ 2017 年各季度 国民生产 总值折线.png')
plt.show()

2000~ 2017年各季度国民生产总值点线图

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'  # 汉字字体,优先使用楷体，如果找不到楷体，则使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 这两行需要手动设置

data = np.load('35data.npz/国民经济核算季度数据.npz',allow_pickle=True)
values = data['values']
plt.figure(figsize=(8, 7))
plt.plot(values[:,0],values[:,2],color='r',linestyle='--',marker='o')
plt.xlabel('年份')
plt.ylabel('生产总值（亿元）')
plt.ylim((0, 225000))
plt.xticks(range(0, 70, 4), values[range(0, 70, 4), 1], rotation=45)
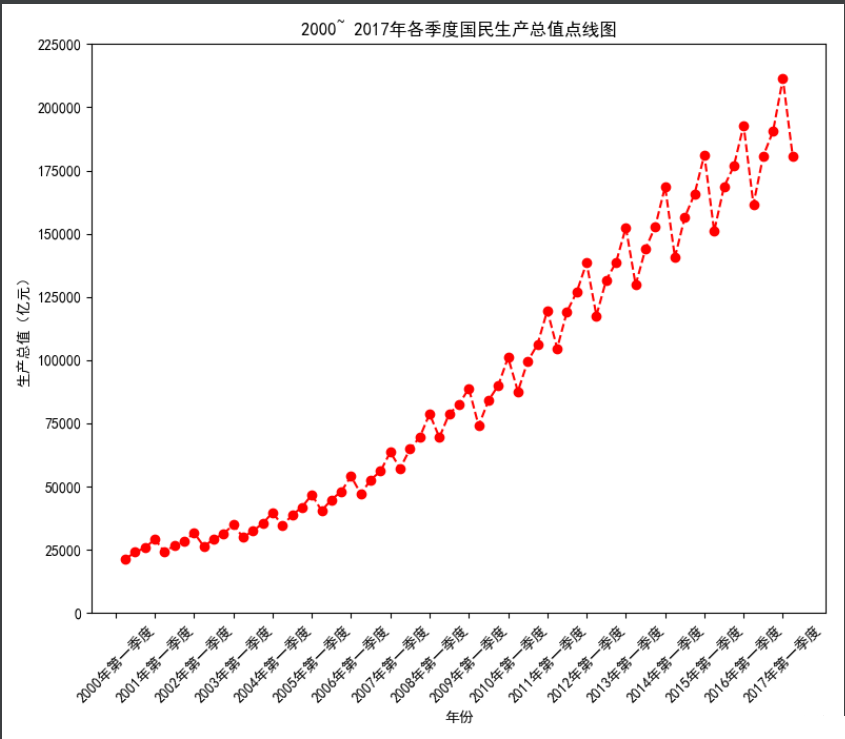
plt.title('2000~ 2017年各季度国民生产总值点线图')
plt.savefig('2000~ 2017年各季度国民生产总值点线图.png')
plt.show()

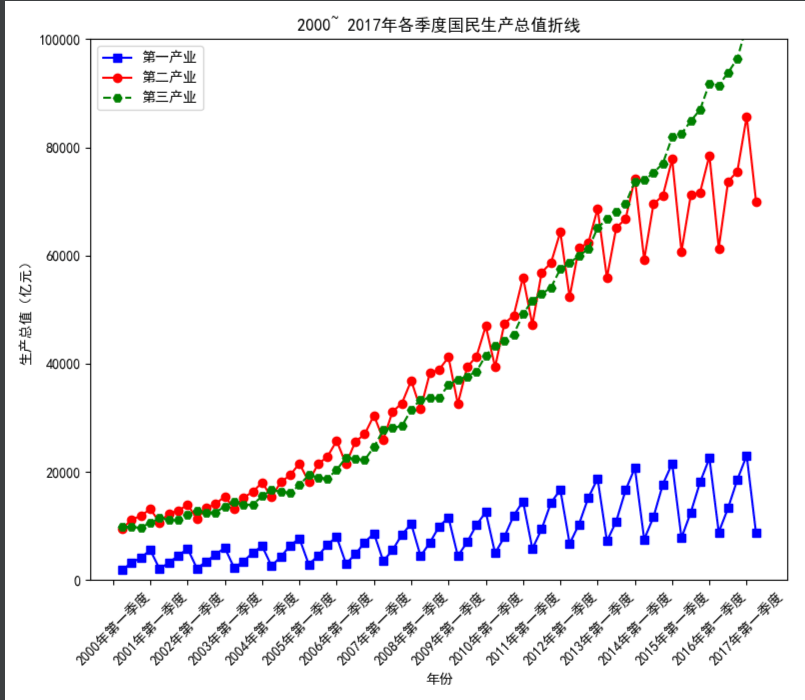
2000~ 2017年各季度国民生产总值折线散点图

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'  # 汉字字体,优先使用楷体，如果找不到楷体，则使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 这两行需要手动设置

data = np.load('35data.npz/国民经济核算季度数据.npz', allow_pickle=True)
values = data['values']
plt.figure(figsize=(8, 7))
plt.plot(values[:, 0], values[:, 3], 'bs-',
         values[:, 0], values[:, 4], 'ro-',
         values[:, 0], values[:, 5], 'gH--')
plt.xlabel('年份')
plt.ylabel('生产总值（亿元）')
plt.ylim((0, 100000))
plt.xticks(range(0, 70, 4), values[range(0, 70, 4), 1], rotation=45)
plt.title('2000~ 2017年各季度国民生产总值折线')
plt.legend(['第一产业','第二产业', '第三产业'])
plt.savefig('2000~ 2017年各季度国民生产总值折线散点图.png')
plt.show()

任务实现

任务1

绘制2000-2017各产业与行业的过敏生产总值散点图：

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'  # 汉字字体,优先使用楷体，如果找不到楷体，则使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 这两行需要手动设置

data = np.load('35data.npz/国民经济核算季度数据.npz', allow_pickle=True)
name = data['columns']
values = data['values']
p = plt.figure(figsize=(12, 12))
# 子图1
ax1 = p.add_subplot(2, 1, 1)
plt.scatter(values[:, 0], values[:, 3], marker='o', c='r')
plt.scatter(values[:, 0], values[:, 4], marker='D', c='b')
plt.scatter(values[:, 0], values[:, 5], marker='v', c='y')
plt.ylabel('生产总值（亿元）')
plt.title('2000-2017年各产业与行业国民生产总值散点图')
plt.legend(['第一产业', '第二产业', '第三产业'])

# 子图2
ax2 = p.add_subplot(2, 1, 2)
plt.scatter(values[:, 0], values[:, 6], marker='o', c='r')
plt.scatter(values[:, 0], values[:, 7], marker='D', c='b')
plt.scatter(values[:, 0], values[:, 8], marker='v', c='y')
plt.scatter(values[:, 0], values[:, 9], marker='8', c='g')
plt.scatter(values[:, 0], values[:, 10], marker='p', c='c')
plt.scatter(values[:, 0], values[:, 11], marker='+', c='m')
plt.scatter(values[:, 0], values[:, 12], marker='s', c='k')
# 绘制散点图
plt.scatter(values[:, 0], values[:, 13], marker='*', c='purple')
# 绘制散点图
plt.scatter(values[:, 0], values[:, 14], marker='d', c='brown')
plt.legend(['农业', '工业', '建筑', '批发', '交通', '餐饮', '金融', '房地产', '其他'])
plt.xlabel('年份')
plt.ylabel('生产总值（亿元）')
plt.xticks(range(0, 70, 4), values[range(0, 70, 4), 1], rotation=45)
plt.savefig('2000~ 2017年各产业与行业各季度国民生产总值散点子图.png')
plt.show()

任务2

绘制2000-2017各产业与行业的过敏生产总值折线图：

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'  # 汉字字体,优先使用楷体，如果找不到楷体，则使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 这两行需要手动设置

data = np.load('35data.npz/国民经济核算季度数据.npz', allow_pickle=True)
name = data['columns']
values = data['values']
p1 = plt.figure(figsize=(8, 7))
# 子图1
ax3 = p1.add_subplot(2, 1, 1)
plt.plot(values[:, 0], values[:, 3], 'b-',
values[:, 0], values[:, 4], 'r--',
values[:, 0], values[:, 5], 'g--')
plt.ylabel('生产总值（亿元）')
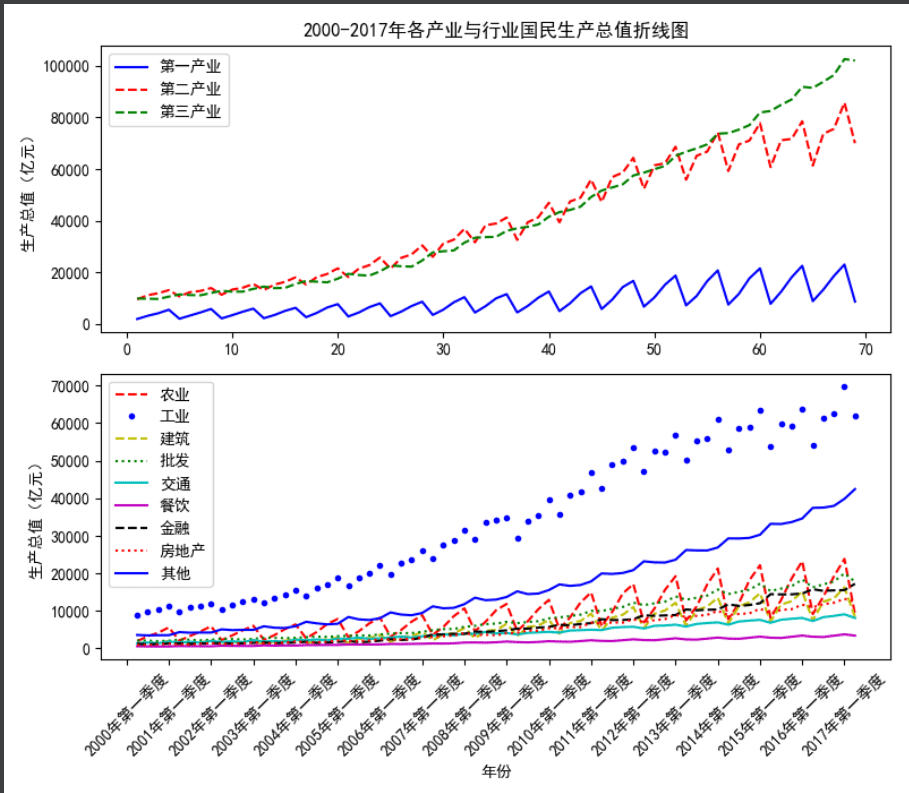
plt.title('2000-2017年各产业与行业国民生产总值折线图')
plt.legend(['第一产业', '第二产业', '第三产业'])

# 子图2
ax4 = p1.add_subplot(2, 1, 2)
plt.plot(values[:, 0], values[:, 6], 'r--',
values[:, 0], values[:, 7], 'b.',
values[:, 0], values[:, 8], 'y--',
values[:, 0], values[:, 9], 'g:',
values[:, 0], values[:, 10], 'c-',
values[:, 0], values[:, 11], 'm-',
values[:, 0], values[:, 12], 'k--',
# 绘制散点图
values[:, 0], values[:, 13], 'r:',
# 绘制散点图
values[:, 0], values[:, 14], 'b-')
plt.legend(['农业', '工业', '建筑', '批发', '交通', '餐饮', '金融', '房地产', '其他'])
plt.xlabel('年份')
plt.ylabel('生产总值（亿元）')
plt.xticks(range(0, 70, 4), values[range(0, 70, 4), 1], rotation=45)
plt.savefig('2000~ 2017年各产业与行业各季度国民生产总值折线子图.png')
plt.show()

分析特征内部数据分布与分散状况

直方图、饼图和箱线图是另外3种数据分析常用的图形，主要用于分析数据内部的分布状态和分散状态。

• 直方图主要用于查看各分组数据的数量分布，以及各个分组数据之间的数量比较。
• 饼图倾向于查看各分组数据在总数据中的占比。箱线图的主要作用是发现整体数据的分布分散情况。 绘制直方图
• 在直方图中可以发现分布表无法发现的数据模式、样本的频率分布和总体的分布

puplot中绘制直方图的函数为bar，基本使用语法如下：

matplotlib.pyplot.bar(left,height,width=0.8,bottom=None,hold=None,data=None,**kwargs)

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'  # 汉字字体,优先使用楷体，如果找不到楷体，则使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 这两行需要手动设置

data = np.load('35data.npz/国民经济核算季度数据.npz', allow_pickle=True)
name = data['columns']
values = data['values']
label = ['第一产业', '第二产业', '第三产业']
plt.figure(figsize=(6, 5))
plt.bar(range(3), values[-2, 3:6], width=0.5)
plt.xlabel('年份')
plt.ylabel('生产总值（亿元）')
plt.title('000~ 2017年各产业与行业各季度国民生产总值直方图')
plt.xticks(range(3), label)
plt.savefig('2000~ 2017年各产业与行业各季度国民生产总值直方图.png')
plt.show()

绘制饼图

饼图(Pie Graph)是将各项的大小与各项总和的比例显示在一张“饼”中，以“饼”的大小来确定每一项的占比。饼图可以比较清楚地反映出部分与部分、部分与整体之间的比例关系，易于显示每组数据相对于总数的大小，而且显示方式直观。

pyplot中绘制饼图的函数为pie，其基本使用语法如下:
matplotlib.pyplot.pie(x,explode=None,labels=Nonecolors=None,autopctNone,pctdistance=0.6shadow=False,labeldistance=1.1,startangle=None,radius=None,counterclock=Truewedgeprops=Nonetextprops=Nonecenter=(0.0)frame=False
hold=Nonedata-None)

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'  # 汉字字体,优先使用楷体，如果找不到楷体，则使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 这两行需要手动设置

data = np.load('35data.npz/国民经济核算季度数据.npz', allow_pickle=True)
name = data['columns']
values = data['values']
label = ['第一产业', '第二产业', '第三产业']
explode = [0.01, 0.01, 0.01]
plt.pie(values[-1, 3:6], explode=explode, labels=label, autopct='%1.1f%%')
plt.figure(figsize=(6, 6))
plt.title('2000~ 2017年各产业与行业各季度国民生产总值饼图')
plt.savefig('2000~ 2017年各产业与行业各季度国民生产总值占比饼图.png')
plt.show()

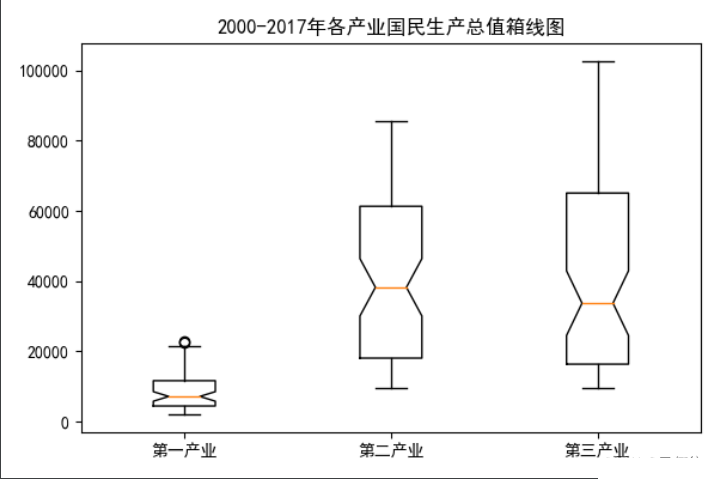
绘制箱线图

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'  # 汉字字体,优先使用楷体，如果找不到楷体，则使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 这两行需要手动设置

plt.figure(figsize=(6, 4))
data = np.load('35data.npz/国民经济核算季度数据.npz', allow_pickle=True)
name = data['columns']
values = data['values']
label = ['第一产业', '第二产业', '第三产业']
gdp = (list(values[:, 3]), list(values[:, 4]), list(values[:, 5]))
plt.boxplot(gdp, notch=True, labels=label, meanline=True)
plt.title('2000-2017年各产业国民生产总值箱线图')
plt.savefig('2000-2017年各产业过敏生产总值箱线图')
plt.show()

任务实现

任务1：

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'  # 汉字字体,优先使用楷体，如果找不到楷体，则使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 这两行需要手动设置

plt.figure(figsize=(6, 6))
data = np.load('35data.npz/国民经济核算季度数据.npz', allow_pickle=True)
name = data['columns']
values = data['values']
label1 = ['第一产业', '第二产业', '第三产业']
label2 = ['农业', '工业', '建筑', '批发', '交通', '餐饮', '金融', '房地产', '其他']
p = plt.figure(figsize=(12, 12,))
# 子图1
ax1 = p.add_subplot(2, 2, 1)
plt.bar(range(3), values[0, 3:6], width=0.5)
plt.xlabel('年份')
plt.ylabel('生产总值（亿元）')
plt.title('2000~ 2017年各产业与行业各季度国民生产总值构成分布直方图')
plt.xticks(range(3), label1)

# 子图2
ax2 = p.add_subplot(2, 2, 2)
plt.bar(range(3), values[0, 3:6], width=0.5)
plt.xlabel('年份')
plt.ylabel('生产总值（亿元）')
plt.title('2000~ 2017年各产业与行业各季度国民生产总值构成分布直方图')
plt.xticks(range(3), label1)
# 子图3
ax3 = p.add_subplot(2, 2, 3)
plt.bar(range(9), values[0, 6:], width=0.5)
plt.xlabel('年份')
plt.ylabel('生产总值（亿元）')
plt.title('2000~ 2017年各产业与行业各季度国民生产总值构成分布直方图')
plt.xticks(range(9), label2)
# 子图4
ax4 = p.add_subplot(2, 2, 4)
plt.bar(range(9), values[0, 6:], width=0.5)
plt.xlabel('年份')
plt.ylabel('生产总值（亿元）')
plt.title('2000~ 2017年各产业与行业各季度国民生产总值构成分布直方图')
plt.xticks(range(9), label2)
plt.savefig('2000~ 2017年各产业与行业各季度国民生产总值构成分布直方图.png')
plt.show()

任务2：

绘制国民生产总值构成分布饼图：

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'  # 汉字字体,优先使用楷体，如果找不到楷体，则使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 这两行需要手动设置

plt.figure(figsize=(6, 6))
data = np.load('35data.npz/国民经济核算季度数据.npz', allow_pickle=True)
name = data['columns']
values = data['values']
label1 = ['第一产业', '第二产业', '第三产业']
label2 = ['农业', '工业', '建筑', '批发', '交通', '餐饮', '金融', '房地产', '其他']

explode1 = [0.01, 0.01, 0.01]
explode2 = [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01]
p = plt.figure(figsize=(12, 12))
# 子图1
ax1 = p.add_subplot(2, 2, 1)
plt.pie(values[0, 3:6], explode=explode1, labels=label1, autopct='%1.1f%%')
plt.title('2000年第一季度国民生产总值产业构成分布饼图')
# 子图2
ax2 = p.add_subplot(2, 2, 2)
plt.pie(values[-1, 3:6], explode=explode1, labels=label1, autopct='%1.1f%%')
plt.title('2000年第一季度国民生产总值产业构成分布饼图')
# 子图3
ax3 = p.add_subplot(2, 2, 3)
plt.pie(values[0, 6:], explode=explode2, labels=label2, autopct='%1.1f%%')
plt.title('2000年第一季度国民生产总值产业构成分布饼图')
# 子图4
ax4 = p.add_subplot(2, 2, 4)
plt.pie(values[-1, 6:], explode=explode2, labels=label2, autopct='%1.1f%%')
plt.title('2000年第一季度国民生产总值产业构成分布饼图')
#保存并显示图形
plt.savefig('国民生产总值产业构成分布饼图.png')
plt.show()

任务3:

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'  # 汉字字体,优先使用楷体，如果找不到楷体，则使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 这两行需要手动设置

plt.figure(figsize=(6, 6))
data = np.load('35data.npz/国民经济核算季度数据.npz', allow_pickle=True)
name = data['columns']
values = data['values']

label1 = ['第一产业', '第二产业', '第三产业']
label2 = ['农业', '工业', '建筑', '批发', '交通', '餐饮', '金融', '房地产', '其他']

gdp1 = (list(values[:, 3]), list(values[:, 4]), list(values[:, 5]))
gdp2 = ([list(values[:, i]) for i in range(6, 15)])
p = plt.figure(figsize=(8, 8))

# 子图1
ax1 = p.add_subplot(2, 1, 1)
plt.boxplot(gdp1, notch=True, labels=label1, meanline=True)
plt.title('2000-2017年各产业国民生产总值箱线图')
plt.ylabel('生产总值（亿元）')
# 子图2
ax2 = p.add_subplot(2, 1, 2)
plt.boxplot(gdp2, notch=True, labels=label2, meanline=True)
plt.title('2000-2017年各产业国民生产总值箱线图')
plt.xlabel('行业')
plt.ylabel('生产总值（亿元）')
plt.savefig('2000-2017年各产业过敏生产总值箱线图.png')
plt.show()

实训

需求说明:

人口数据总共拥有6个特征，分别为年末总人口、男性人口、女性人口、城镇人口、乡村人口和年份。查看各个特征随着时间推移发生的变化情况可以分析出未来男女人口比例、城乡人口变化的方向。

具体步骤:

(1)使用NumPy库读取人口数据。
(2)创建画布，并添加子图。
(3)在两个子图上分别绘制散点图和折线图。
(4)保存，显示图片。
(5)分析未来人口变化趋势。

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'  # 汉字字体,优先使用楷体，如果找不到楷体，则使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 这两行需要手动设置

data = np.load('Data/populations.npz', allow_pickle=True)
feature_names = data['feature_names']
data = data['data']
# for i in data:
#     print(i)
p = plt.figure(figsize=(10, 9))
# 子图1
ax1 = p.add_subplot(2, 1, 1)
plt.scatter(range(data.shape[0] - 2), data[:-2, 1], marker='o', c='r')
plt.scatter(range(data.shape[0] - 2), data[:-2, 2], marker='D', c='b')
plt.scatter(range(data.shape[0] - 2), data[:-2, 3], marker='v', c='y')
plt.scatter(range(data.shape[0] - 2), data[:-2, 4], marker='+', c='c')
plt.scatter(range(data.shape[0] - 2), data[:-2, 5], marker='p', c='g')
plt.xlabel('时间-年份')
plt.ylabel('人口数（万人）')
plt.xticks(range(data.shape[0] - 2), data[:-2, 0], rotation=45)
plt.title('1996~2015年各特征人口变化散点图')
plt.legend(['年末人口', '男性人口', '女性人口', '城镇人口', '乡村人口和年份', '年份'])
# 子图2
ax2 = p.add_subplot(2, 1, 2)
plt.plot(range(data.shape[0] - 2), data[:-2, 1], c='r', linestyle='--')
plt.plot(range(data.shape[0] - 2), data[:-2, 2], c='b', linestyle='--')
plt.plot(range(data.shape[0] - 2), data[:-2, 3], c='y', linestyle='--')
plt.plot(range(data.shape[0] - 2), data[:-2, 4], c='g', linestyle='--')
plt.plot(range(data.shape[0] - 2), data[:-2, 5], c='c', linestyle='--')
plt.legend(['年末总人口', '男性人口', '女性人口', '城镇人口', '乡村人口'])
plt.xlabel('时间-年份')
plt.ylabel('人口数（万人）')
plt.xticks(range(data.shape[0] - 2), data[:-2, 0], rotation=45)
plt.title('1996-2015年各特征人口数折线图')
plt.show()

实训2

需求说明:

通过绘制各年份男女人口数目及城乡人口数目的直方图，男女人口比例及城乡人口比例的饼图可以发现人口结构的变化。而绘制每个特征的箱线图则可以发现不同特征增长或者减少的速率是否变得缓慢。

实现步骤:

(1)创建3幅画布并添加对应数目的子图。
(2)在每一幅子图上绘制对应的图形。
(3)保存和显示图形。
(4)根据图形，分析我国人口结构变化情况以及变化速率的增减状况。

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'  # 汉字字体,优先使用楷体，如果找不到楷体，则使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 这两行需要手动设置

data = np.load('Data/populations.npz', allow_pickle=True)
feature_names = data['feature_names']
data = data['data']
pt = plt.figure(figsize=(12, 11))

# 创建子图1
ax1 = pt.add_subplot(2, 1, 1)
plt.bar(range(data.shape[0] - 2), data[:-2, 2], width=0.5)
plt.xticks(range(data.shape[0] - 2), data[:-2, 0], rotation=45)
plt.xlabel('1996~2015年男性人口总数')
plt.ylabel('人口数据特征')
plt.title('1996~2015年人口数据特征间的关系的直方图')

# 创建子图2
ax2 = pt.add_subplot(2, 2, 2)
plt.bar(range(data.shape[0] - 2), data[:-2, 3], width=0.5)
plt.xticks(range(data.shape[0] - 2), data[:-2, 0], rotation=45)
plt.xlabel('1996-2015年女性人口数目')
plt.ylabel('人口数目（万人）')

# 创建子图3
ax3 = pt.add_subplot(2, 2, 3)
plt.bar(range(data.shape[0] - 2), data[:-2, 4], width=0.5)
plt.xticks(range(data.shape[0] - 2), data[:-2, 0], rotation=45)
plt.xlabel('1996-2015年城市人口数目')
plt.ylabel('人口数目（万人）')

# 创建子图4
ax4 = pt.add_subplot(2, 2, 4)
plt.bar(range(data.shape[0] - 2), data[:-2, 5], width=0.5)
plt.xticks(range(data.shape[0] - 2), data[:-2, 0], rotation=45)
plt.xlabel('1996-2015年乡村人口数目')
plt.ylabel('人口数目（万人）')
plt.show()

# 绘制饼图
import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'  # 汉字字体,优先使用楷体，如果找不到楷体，则使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 这两行需要手动设置

data = np.load('Data/populations.npz', allow_pickle=True)
feature_names = data['feature_names']
data = data['data']

pt2 = plt.figure(figsize=(12, 10))
# 创建子图1
ax1 = pt2.add_subplot(2, 2, 1)
plt.pie(data[:-2, 2], labels=data[:-2, 0], autopct='%1.1f%%')
plt.title('1996-2015年男性人口比例')

# 创建子图2
ax2 = pt2.add_subplot(2, 2, 2)
plt.pie(data[:-2, 3], labels=data[:-2, 0], autopct='%1.1f%%')
plt.title('1996-2015年女性人口比例')
# 创建子图3
ax3 = pt2.add_subplot(2, 2, 3)
plt.pie(data[:-2, 4], labels=data[:-2, 0], autopct='%1.1f%%')
plt.title('1996-2015年城市人口比例')

# 创建子图4
ax4 = pt2.add_subplot(2, 2, 4)
plt.pie(data[:-2, 5], labels=data[:-2, 0], autopct='%1.1f%%')
plt.title('1996-2015年乡村人口比例')
plt.show()

# 绘制箱线图
import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'  # 汉字字体,优先使用楷体，如果找不到楷体，则使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 这两行需要手动设置

data = np.load('Data/populations.npz', allow_pickle=True)
feature_names = data['feature_names']
data = data['data']

pt3 = plt.figure(figsize=(12, 10))
label = ['年末总人口', '男性人口', '女性人口', '城镇人口', '乡村人口']
plt.boxplot(([list(data[:-2, i]) for i in range(1, 6)]), labels=label, meanline=True)
plt.title('1996-2015年各特征人口数线箱图')
plt.ylabel('人口数（万人）')
plt.show()

到此这篇关于Python数据分析应用之Matplotlib数据可视化详情的文章就介绍到这了,更多相关Python Matplotlib可视化内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！