C++实现二分法求方程近似解

二分法是一种求解方程近似根的方法。对于一个函数 f(x)f(x)，使用二分法求 f(x)f(x) 近似解的时候，我们先设定一个迭代区间（在这个题目上，我们之后给出了的两个初值决定的区间 [-20,20]），区间两端自变量 x 的值对应的 f(x) 值是异号的，之后我们会计算出两端 x 的中点位置 x' 所对应的 f(x') ，然后更新我们的迭代区间，确保对应的迭代区间的两端 x 的值对应的 f(x) 值还会是异号的。

重复这个过程直到我们某一次中点值 x' 对应的 f(x') < f(x′)<ϵ （题目中可以直接用EPSILON）就可以将这个 x′ 作为近似解返回给 main 函数了。

例如：

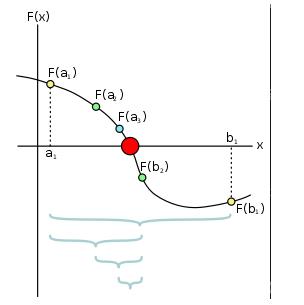
上面所示的一个迭代过程的第一次的迭代区间是 [a1​,b1​]，取中点 b2​，然后第二次的迭代区间是 [a1​,b2​]，再取中点 a2​，然后第三次的迭代区间是 [a2​,b2​]，然后取 a3​，然后第四次的迭代区间是[a3​,b2​]，再取红色中点 c，我们得到发现 f(c) 的值已经小于ϵ，输出c 作为近似解。

在这里，我们将用它实现对形如 px+q=0 的一元一次方程的求解。

在这里，你完成的程序将被输入两个正整数 p 和 q（你可以认为测评机给出的 0<∣p∣≤1000 且0<∣q∣≤1000），程序需要用二分法求出 px+q=0 的近似解。

输入格式

测评机会反复运行你的程序。每次程序运行时，输入为一行，包括一组被空格分隔开的符合描述的正整数 p 和 q。你可以认为输入数据构成的方程 px+q=0 都是有解且解在[−20,20] 的区间内。

输出格式

输出为一行，包括一个数字。为方程 px+q=0 的近似解。请使用四舍五入的方式保留小数点后 4 位小数。

样例输入1

55 9

样例输出1

-0.1636

样例输入2

-22 4

样例输出2

0.1818

代码：

#include <cstdio>
#include <cmath>
#define EPSILON 1e-7

double bisection(int p, int q, double (*func)(int, int, double));
double f(int p, int q, double x);
int main() {
    int p;
    int q;
    scanf("%d %d", &p, &q);
    printf("%.4lf\n", bisection(p, q, f));
    return 0;
}

double bisection(int p, int q, double (*func)(int, int, double)) {
    double x1 = -20;
 double x2 = 20;
 double x = 0;
 while(fabs((*func)(p,q,x))>EPSILON)
 {
  x = (x1+x2)/2.0;
  double fx1 = (*func)(p,q,x1);
  double fx =  (*func)(p,q,x);
  if(fx*fx1>0)
  {x1 = x;}
  else
  {x2 = x;}

 }
 return x;
}

double f(int p, int q, double x) {
    return p * x + q;
}

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。

赞 (0)

相关推荐

  • C++实现二分法求连续一元函数根

    本文实例为大家分享了C++实现二分法求连续一元函数根的具体代码,供大家参考,具体内容如下 设计一个用二分法求连续一元函数根的通用函数solve 此函数有三个参数: 第一个是函数指针,指向所要求根的连续函数 第二.三个参数指出根的区间,且确保函数在区间的两个端点异号 函数的返回值为求得的解 要求编写main函数如下: double fun(double x) { double y; y=4*pow(x,3)-6*pow(x,2)+3*x-2; return y; } int main() { co

  • C++二分法在数组中查找关键字的方法

    本文实例讲述了C++二分法在数组中查找关键字的方法.分享给大家供大家参考.具体如下: /* 此程序演示了二分法查找算法(针对按从小到大排列的数组)的实现. */ #include <iostream> using namespace std; /* 功能: 实现数组的二分法查找(只算法只适合按从小到大排列的数组) 返回值:关键字在数组中的下标, 返回-1表示未找到 a[]: 要搜索的数组 len: 数组元素个数 key: 要查找的关键字 */ int binSearch(int a[], in

  • C++实现二分法求方程近似解

    C++实现二分法求方程近似解

    二分法是一种求解方程近似根的方法.对于一个函数 f(x)f(x),使用二分法求 f(x)f(x) 近似解的时候,我们先设定一个迭代区间(在这个题目上,我们之后给出了的两个初值决定的区间 [-20,20]),区间两端自变量 x 的值对应的 f(x) 值是异号的,之后我们会计算出两端 x 的中点位置 x' 所对应的 f(x') ,然后更新我们的迭代区间,确保对应的迭代区间的两端 x 的值对应的 f(x) 值还会是异号的. 重复这个过程直到我们某一次中点值 x' 对应的 f(x') < f(x′)<

  • C语言二分法求解方程根的两种方法

    本文实例为大家分享了C语言二分法求解方程根的具体代码,供大家参考,具体内容如下 对于二分法求根,其实和弦截法思想很像,甚至更简单. 原理:先看如下的图 A,B两个点为跟的一个边界,通过一直缩小跟的边界,从而获取跟的值. (1)知道函数(即方程的式子),这个好说,题上都有 (2)循环的输入A,B的横坐标的值,即x1,x2的初值,直到f(x1)与f(x2)的乘积为负数才停止.(必须保证方程的跟在(x1,x2)区间)这样的x1,x2的初值才有意义. (3)令xx=(x1+x2)/2;(即中值),若f(

  • Python用二分法求平方根的案例

    我就废话不多说了,大家还是直接看代码吧~ def sq2(x,e): e = e #误差范围 low= 0 high = max(x,1.0) #处理大于0小于1的数 guess = (low + high) / 2.0 ctr = 1 while abs(guess**2 - x) > e and ctr<= 1000: if guess**2 < x: low = guess else: high = guess guess = (low + high) / 2.0 ctr += 1

  • 二分法求多项式在-10 10间值的实现代码

    代码如下所示: 复制代码 代码如下: #include <stdio.h>#include <math.h> int main(){ float  x0,x1,x2,f1,f2,f0;  //x1,x2求两端值 do {  printf("input 2 num:\n");  scanf("%f %f",&x1,&x2);  f1=x1*((2*x1-4)*x1+3)-6;  f2=x2*((2*x2-4)*x2+3)-6; 

  • Python编程实现二分法和牛顿迭代法求平方根代码

    求一个数的平方根函数sqrt(int num) ,在大多数语言中都提供实现.那么要求一个数的平方根,是怎么实现的呢? 实际上求平方根的算法方法主要有两种:二分法(binary search)和牛顿迭代法(Newton iteration) 1:二分法 求根号5 a:折半: 5/2=2.5 b:平方校验: 2.5*2.5=6.25>5,并且得到当前上限2.5 c:再次向下折半:2.5/2=1.25 d:平方校验:1.25*1.25=1.5625<5,得到当前下限1.25 e:再次折半:2.5-(

  • C语言求Fibonacci斐波那契数列通项问题的解法总结

    C语言求Fibonacci斐波那契数列通项问题的解法总结

    一:递归实现   使用公式f[n]=f[n-1]+f[n-2],依次递归计算,递归结束条件是f[1]=1,f[2]=1. 二:数组实现   空间复杂度和时间复杂度都是0(n),效率一般,比递归来得快. 三:vector<int>实现   时间复杂度是0(n),时间复杂度是0(1),就是不知道vector的效率高不高,当然vector有自己的属性会占用资源. 四:queue<int>实现   当然队列比数组更适合实现斐波那契数列,时间复杂度和空间复杂度和vector<int&g

  • 求斐波那契(Fibonacci)数列通项的七种实现方法

    求斐波那契(Fibonacci)数列通项的七种实现方法

    一:递归实现使用公式f[n]=f[n-1]+f[n-2],依次递归计算,递归结束条件是f[1]=1,f[2]=1.二:数组实现空间复杂度和时间复杂度都是0(n),效率一般,比递归来得快.三:vector<int>实现时间复杂度是0(n),时间复杂度是0(1),就是不知道vector的效率高不高,当然vector有自己的属性会占用资源.四:queue<int>实现当然队列比数组更适合实现斐波那契数列,时间复杂度和空间复杂度和vector<int>一样,但队列太适合这里了,

  • python numpy.power()数组元素求n次方案例

    如下所示: numpy.power(x1, x2) 数组的元素分别求n次方.x2可以是数字,也可以是数组,但是x1和x2的列数要相同. >>> x1 = range(6) >>> x1 [0, 1, 2, 3, 4, 5] >>> np.power(x1, 3) array([ 0, 1, 8, 27, 64, 125]) >>> x2 = [1.0, 2.0, 3.0, 3.0, 2.0, 1.0] >>> np.

  • C++实现LeetCode( 69.求平方根)

    [LeetCode] 69. Sqrt(x) 求平方根 Implement int sqrt(int x). Compute and return the square root of x, where x is guaranteed to be a non-negative integer. Since the return type is an integer, the decimal digits are truncated and only the integer part of the

随机推荐