Python数据结构之图的存储结构详解

一、图的定义

图是一种比树更复杂的一种数据结构，在图结构中，结点之间的关系是任意的，任意两个元素之间都可能相关，因此，它的应用极广。图中的数据元素通常被称为顶点 ( V e r t e x ) (Vertex) (Vertex)， V V V是顶点的有穷非空集合， V R VR VR是两个顶点之间的关系的集合(可以为空)，可以表示为图 G = { V , { V R } } G=\{V,\{VR\}\} G={V,{VR}}。

二、相关术语

2.1 无向图

给定图 G = { V , { E } } G=\{V,\{E\}\} G={V,{E}}，若该图中每条边都是没有方向的，则称其为无向图 ( U n d i g r a p h ) (Undigraph) (Undigraph)。对图 G G G中顶点 v v v和顶点 w w w的关系，可用无序对 ( v , w ) (v,w) (v,w)表示，它是连接 v v v和 w w w的一条边 ( E d g e ) (Edge) (Edge)。

2.2 有向图

给定图 G = { V , { A } } G=\{V,\{A\}\} G={V,{A}}，若该图中每条边都是有方向的，则称其为有向图 ( D i g r a p h ) (Digraph) (Digraph)。对图 G G G中顶点 v v v和顶点 w w w的关系，可用有序对 < v , w > <v,w> <v,w>表示，它是从 v v v到 w w w的一条弧 ( A r c ) (Arc) (Arc)，其中 v v v被称为弧尾 ( T a i l ) (Tail) (Tail)， w w w被称为弧头 ( H e a d ) (Head) (Head)。

  弧尾也叫初始点 ( I n i t i a l (Initial (Initial N o d e ) Node) Node)，弧头也叫终端点 ( T e r m i n a l (Terminal (Terminal N o d e ) Node) Node)。

2.3 完全图

对于任一无向图，若其顶点的总数目为 n n n，边的总数目为 e = n ( n − 1 ) 2 e=\frac {n(n-1)} {2} e=2n(n−1)​，则称其为完全图 ( C o m p l e t e d (Completed (Completed G r a p h ) Graph) Graph)。

2.4 有向完全图

对于任一有向图，若其顶点的总数目为 n n n，边的总数目为 e = n ( n − 1 ) e=n(n-1) e=n(n−1)，则称其为有向完全图。

2.5 稀疏图和稠密图

对于具有 n n n个顶点， e e e条边或弧的图来说，若 e e e很小，比如 e < n log ⁡ n e<n\log n e<nlogn，则称其为稀疏图 ( S p a r s e (Sparse (Sparse G r a p h ) Graph) Graph)，反之称其为稠密图 ( D e n s e (Dense (Dense G r a p h ) Graph) Graph)。

2.6 权和网

赋予图中边或弧的数值称为权 ( W e i g h t ) (Weight) (Weight)，它可以表示从一个顶点到另一个顶点的距离；带权的图称为网 ( N e t w o r k ) (Network) (Network)。

2.7 稀疏网和稠密网

带权的稀疏图、稠密图称为稀疏网、稠密网。

2.8 子图

对于图 G = { V , { E } } G=\{V,\{E\}\} G={V,{E}}和图 G ′ = { V ′ , { E ′ } } G'=\{V',\{E'\}\} G′={V′,{E′}}，若 V ′ ⊆ V V'\subseteq V V′⊆V且 E ′ ⊆ E E'\subseteq E E′⊆E，则称 G ′ G' G′为 G G G的子图 ( S u b g r a p h ) (Subgraph) (Subgraph)。

2.9 邻接点

对于无向图 G = { V , { E } } G=\{V,\{E\}\} G={V,{E}}，若 v ∈ V v\in V v∈V、 w ∈ V w\in V w∈V且 ( v , w ) ∈ E (v,w)\in E (v,w)∈E，则称顶点 v v v和顶点 w w w互为邻接点 ( A d j a c e n t ) (Adjacent) (Adjacent)，并称边 ( v , w ) (v,w) (v,w)依附 ( I n c i d e n t ) (Incident) (Incident)于顶点 v v v和顶点 w w w，或称边 ( v , w ) (v,w) (v,w)与顶点 v v v和顶点 w w w相关联。

对于有向图 G = { V , { A } } G=\{V,\{A\}\} G={V,{A}}，若 v ∈ V v\in V v∈V、 w ∈ V w\in V w∈V且 < v , w > ∈ A <v,w>\in A <v,w>∈A，则称顶点 v v v邻接到顶点 w w w，顶点 w w w邻接自顶点 v v v，并称弧 < v , w > <v,w> <v,w>与顶点 v v v和顶点 w w w相关联。

2.10 度、入度与出度

在无向图中，顶点 v v v的度 ( D e g r e e ) (Degree) (Degree)等于与该顶点相关联的边的数目，记为 T D ( v ) TD(v) TD(v)。

在有向图中，顶点 v v v的度等于该顶点的入度与出度之和，记为 T D ( v ) = I D ( v ) + O D ( v ) TD(v)=ID(v)+OD(v) TD(v)=ID(v)+OD(v)，其中顶点 v v v的入度 ( I n D e g r e e ) (InDegree) (InDegree)为以该顶点为弧头的弧的数目，记为 I D ( v ) ID(v) ID(v)，顶点 v v v的出度 ( O u t D e g r e e ) (OutDegree) (OutDegree)为以该顶点为弧尾的弧的数目，记为 O D ( v ) OD(v) OD(v)。

2.11 路径、简单路径与路径长度

路径 ( P a t h ) (Path) (Path)是任意两个有关联的顶点之间的边或弧，在图 G = { V , { V R } } G=\{V,\{VR\}\} G={V,{VR}}中，顶点 v 1 v_1 v1​到顶点 v n v_n vn​的路径是一个顶点序列 ( v 1 , v 2 , … , v i , v j , … , v n ) (v_1,v_2,\dots,v_i,v_j,\dots,v_n) (v1​,v2​,…,vi​,vj​,…,vn​)，对于上述序列中的任意相邻的顶点 v i v_i vi​和 v j v_j vj​，若图 G G G是无向图，则有 ( v , w ) ∈ E (v,w)\in E (v,w)∈E，若图 G G G是有向图，则有 < v , w > ∈ A <v,w>\in A <v,w>∈A。

对于给定的一条路径，若该路径对应的序列中的顶点不重复，则称为该路径为简单路径。

路径上边或弧的数目称为路径长度。

2.12 回路与简单回路

若某一路径中的第一个顶点和最后一个顶点相同，则称该路径为回路，也称为环 ( C y c l e ) (Cycle) (Cycle)。

在某一回路中，若除去第一个顶点和最后一个顶点外，其余顶点均不重复，则称为该回路为简单回路，也称为简单环。

2.13 连通图与连通分量

在无向图中，若从顶点 v v v到顶点 w w w有路径，则称为 v v v到 w w w是连通的，若该图中的任意两个顶点间都是连通的，则称该图为连通图 ( C o n n e c t e d (Connected (Connected G r a p h ) Graph) Graph)。无向图中的极大连通子图称为连通分量 ( C o n n e c t e d (Connected (Connected C o m p o n e n t ) Component) Component)。这里的极大就是尽可能地包含更多的顶点。

2.14 强连通图与强连通分量

在有向图中，若从顶点 v v v到顶点 w w w有路径，从顶点 w w w到顶点 v v v也有路径，则称为 v v v和 w w w是强连通的，若该图中的任意两个顶点间都是强连通的，则称该图为强连通图。有向图中的极大连通子图称为强连通分量。

2.15 生成树、最小生成树与生成森林

具有 n n n个顶点的连通图的极小连通子图称为生成树，生成树包含这一连通图的 n n n个顶点和 n − 1 n-1 n−1条边。这里的极小是尽可能少地包含边。

通常把各边带权的连通图称为连通网，在连通网的所有生成树中，对每一棵生成树的各边权值求和，其中权值最小的生成树称为该连通网的最小生成树。

非连通图的各连通分量的生成树组成的森林称为生成森林。

3. 图的性质

3.1 性质1

若图中有 n n n个顶点 v 1 , v 2 , … , v n v_1,v_2,\dots,v_n v1​,v2​,…,vn​， e e e条边或弧，其中顶点的度分别为 T D ( v 1 ) , T D ( v 2 ) , … , T D ( v n ) TD(v_1),TD(v_2),\dots,TD(v_n) TD(v1​),TD(v2​),…,TD(vn​)，则有
e = 1 2 ∑ i = 1 n T D ( v i ) e=\frac {1} {2} \sum_{i=1} ^ {n} TD(v_i) e=21​i=1∑n​TD(vi​)

3.2 性质2

一棵有 n n n个顶点的生成树有且仅有 n − 1 n-1 n−1条边。

4. 图的存储结构

4.1 邻接矩阵

用于无向图、有向图

在存储含有 n n n个结点的图 G = { V , { V R } } G=\{V,\{VR\}\} G={V,{VR}}时，将图中的所有顶点存储在长度为 n n n的一维数组中，将图中边或弧的信息存储在 n × n n\times n n×n的二维数组中，我们称这个二维的数组为邻接矩阵。假设图 G G G中顶点 v v v和顶点 w w w在一维数组中的下标分别为 i i i、 j j j，则该图对应各邻接矩阵定义如下：

若该图为无向图或有向图，则
A r c s [ j ] [ j ] = { 1 , ( v , w ) ∈ E 或 < v , w > ∈ A 0 , 其 他 Arcs[j][j]=\begin{cases} 1, & (v,w)\in E或<v,w>\in A\\ \\ 0, & 其他 \end{cases} Arcs[j][j]=⎩⎪⎨⎪⎧​1,0,​(v,w)∈E或<v,w>∈A其他​  若该图为无向网或有向网，则
A r c s [ j ] [ j ] = { w i j , ( v , w ) ∈ E 或 < v , w > ∈ A ∞ , 其 他 Arcs[j][j]=\begin{cases} w_{ij}, & (v,w)\in E或<v,w>\in A\\ \\ \infty, & 其他 \end{cases} Arcs[j][j]=⎩⎪⎨⎪⎧​wij​,∞,​(v,w)∈E或<v,w>∈A其他​  其中， w i j w_{ij} wij​为边或弧对应的权值。

定义图中的顶点：

class VertexMatrix(object):
    """
    图的一个顶点
    """
    def __init__(self, data):
        self.data = data
        self.info = None

定义图：

class GraphMatrix(object):
    """
    图的邻接矩阵
    """
    def __init__(self, kind):
        # 图的类型: 无向图, 有向图, 无向网, 有向网
        # kind: Undigraph, Digraph, Undinetwork, Dinetwork,
        self.kind = kind
        # 顶点表
        self.vertexs = []
        # 边表, 即邻接矩阵, 是个二维的
        self.arcs = []
        # 当前顶点数
        self.vexnum = 0
        # 当前边(弧)数
        self.arcnum = 0

无向图及其邻接矩阵、有向网及其邻接矩阵如下：
A r c s = [ 0 1 0 1 1 0 0 1 0 0 0 1 1 1 1 0 ] A r c s = [ ∞ 1 2 ∞ ∞ ∞ 3 ∞ ∞ ∞ ∞ 4 ∞ ∞ ∞ ∞ ] Arcs=\begin{bmatrix} 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 \end{bmatrix} Arcs=\begin{bmatrix} \infty & 1 & 2 & \infty \\ \infty & \infty & 3 & \infty \\ \infty & \infty & \infty & 4 \\ \infty & \infty & \infty & \infty \end{bmatrix} Arcs=⎣⎢⎢⎡​0101​1001​0001​1110​⎦⎥⎥⎤​Arcs=⎣⎢⎢⎡​∞∞∞∞​1∞∞∞​23∞∞​∞∞4∞​⎦⎥⎥⎤

​

邻接矩阵的特点如下：

(1) 由于在创建邻接矩阵时，输入顶点的顺序不同，其相应的邻接矩阵也是不同的；

(2) 对于含有 n n n个顶点的图，其邻接矩阵一定是 n × n n\times n n×n的二维数组；

(3) 无向图的邻接矩阵具有对称性，可采用压缩存储的方式存储；

(4) 对于无向图，若某一顶点 v v v在一维数组中的下标为 i i i，则该顶点的度为邻接矩阵的第 i + 1 i+1 i+1行中值为1的元素的总数目；

(5) 对于有向图，若某一顶点 v v v在一维数组中的下标为 i i i，则该顶点的出度为邻接矩阵的第 i + 1 i+1 i+1行中值为1的元素的总数目，入度为邻接矩阵的第 i + 1 i+1 i+1列中值为1的元素的总数目。

构造一个具有 n n n个顶点 e e e条边的无向网的时间复杂度为 O ( n 2 + n e ) O(n^2+ne) O(n2+ne)，其中对邻接矩阵的初始化使用了 O ( n 2 ) O(n^2) O(n2)的时间。

4.2 邻接表

用于无向图、有向图

使用邻接表存储图时，将图分为两个部分：

第一部分为图中每一个顶点及与该顶点相关联的第一条边或弧，可以这样定义：

class VertexAdjacencyList(object):
    """
    图的一个顶点
    """
    def __init__(self, data):
        self.data = data
        # 与该顶点相连的第一条边FirstArc
        self.FirstArc = None

使用data域来存储图中的每一个顶点，FirstArc域来存储与该顶点相关联的第一条弧或边，通常情况下指向第二部分单链表的第一个结点。

第二部分为用一个结点来存储图中的每一条边或弧，该结点由adjacent域、info域和NextArc域组成，这些结点形成了单链表。这部分结点可以这样定义：

class ArcAdjacencyList(object):
    """
    图的一个边(弧)
    """
    def __init__(self, adjacent):
        # 邻接点或弧头, 与该顶点相连的另一顶点的index
        self.adjacent = adjacent
        self.info = None
        # 与该边(弧)依附于相同顶点的下一条边(弧)NextArc
        self.NextArc = None

根据上面图的邻接表可以这样定义：

class GraphAdjacencyList(object):
    """
    图的邻接表
    """
    def __init__(self, kind):
        # 图的类型: 无向图, 有向图, 无向网, 有向网
        # kind: Undigraph, Digraph, Undinetwork, Dinetwork,
        self.kind = kind
        # 邻接表
        self.vertices = []
        # 当前顶点数
        self.vexnum = 0
        # 当前边(弧)数
        self.arcnum = 0

无向图及其邻接表：

有向网及其邻接表、逆邻接表：

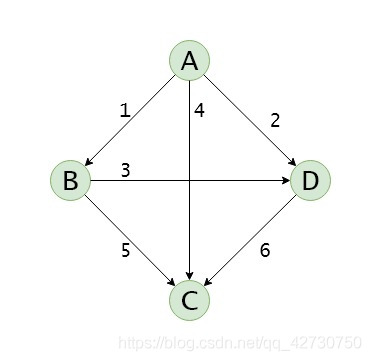
邻接表的特点如下：

(1) 由于存储边或弧通过不同的连接顺序会形成不同的单链表，所以图的邻接表不是唯一的；

(2) 对于具有 e e e条边的无向图，使用邻接表存储时需要 2 e 2e 2e个结点来存储图的边，而对于具有 e e e条弧的有向图，使用邻接表存储时需要 e e e个结点来存储图的弧；

(3) 对于具有 n n n个顶点 e e e条边或弧的稀疏图而言，若采用邻接矩阵存储，则需要 n 2 n^2 n2个存储空间来存储图的边或弧，而采用邻接表存储时，则至多需要 2 e 2e 2e个结点存储图的边或弧，所以稀疏图的存储使用邻接表会更节省空间；

(4) 对于无向图，顶点的度等于该顶点对应的单链表中结点的总数目；

(5) 对于有向图，若某一顶点在数组中的下标为 i i i，则该顶点的出度为该顶点对应的单链表中结点的总数目，入度为邻接表中adjacent域内值为 i i i的结点的总数目。
在使用邻接表存储图时，计算图中的某一顶点的出度很容易，但是在计算其入度时，最坏的情况需要遍历整个邻接表。因此，有时为了方便计算顶点的入度，可以为该图建立一个逆邻接表。

在建立邻接表或逆邻接表时，如输入的顶点信息为顶点的编号，则建立邻接表或逆邻接表的时间复杂度为 O ( n + e ) O(n+e) O(n+e)，否则，需要通过查找才能确定顶点在图中的位置，对应的时间复杂度为 O ( n e ) O(ne) O(ne)。

4.3 十字链表

用于有向图

十字链表通常用于有向图，可以将它看成邻接表和逆邻接表的结合。同样分为两个部分，即顶点结点部分和弧部分，通常将顶结点存储在数组中，弧结点存储在单链表中。

顶点结点包含data域、FirstIn域和FirstOut域，其中data域存储顶点的值，FirstIn域指向以当前顶点为弧头的第

一条弧和FirstOut域指向以当前顶点为弧尾的第一条弧。
弧结点包含TailVertex域、HeadVertex域、HeadLink域、TailLink域和info域，其中TailVertex域存储当前弧的弧尾在数组中的下标，HeadVertex域存储当前弧的弧头在数组中的下标，HeadLink域指向与当前弧有相同弧头的下一条弧，TailLink域指向与当前弧有相同弧尾的下一条弧，info域存储当前弧的其他信息。

顶点结点定义如下：

class VertexOrthogonalList(object):
    """
    有向图的一个顶点
    """
    def __init__(self, data):
        self.data = data
        # 以该顶点为弧头的第一条弧FirstIn
        self.FirstIn= None
        # 以该顶点为弧尾的第一条弧FirstOut
        self.FirstOut= None

弧结点定义如下：

class ArcOrthogonalList(object):
    """
    有向图的一条弧
    """
    def __init__(self):
        # 当前弧中弧头在数组中的下标HeadVertex
        self.HeadVertex = None
        # 当前弧中弧尾在数组中的下标TailVertex
        self.TailVertex = None
        # 与当前弧有相同弧头的下一条弧HeadLink
        self.HeadLink = None
        # 与当前弧有相同弧尾的下一条弧TailLink
        self.TailLink = None
        self.info = None

十字链表表示的有向图定义如下：

class GraphOrthogonalList(object):
    """
    有向图的十字链表
    """
    def __init__(self):
        # 十字链表
        self.vertices = []
        # 当前顶点数
        self.vexnum = 0
        # 当前边(弧)数
        self.arcnum = 0

有向图及其十字链表：

4.4 邻接多重表

用于无向图

在使用邻接表存储无向图时，图的每一条边都对应两个结点，由于这两个结点属于两个不同的邻接表，所以在进行删除操作时需要对邻接表的两条单链表进行操作，比较麻烦，所有引出了邻接多重表。邻接多重表同样分为两个部分，即顶点结点和边结点，通常将顶点结点存储在数组中，边结点存储在单链表中。

顶点结点包含data域和FirstEdge域，其中data域存储顶点的值，FirstEdge域指向与当前顶点相关联的第一条边。

边结点包含mark域、VertexOne域、NextEdgeOne域、VertexTwo域、NextEdgeTwo域和info域，其中mark域用于标记当前是否被访问，VertexOne域和VertexTwo域分别存储当前边的两个顶点在数组中的下标，NextEdgeOne域指向与VertexOne域对应的顶点相关联的下一条边，NextEdgeTwo域指向与VertexTwo域对应的顶点相关联的下一条边，info域存储当前边的其他信息。

顶点结点定义如下：

class VertexAdjacencyMultitable(object):
    """
    无向图的一个顶点
    """
    def __init__(self, data):
        self.data = data
        # 与该顶点相连的第一条边FirstEdge
        self.FirstEdge = None

边结点定义如下：

class Edge(object):
    """
    无向图的邻接多重表
    """
    def __init__(self):
        # 用来标记当前边是否已被访问过
        self.mark = None
        # 该边的两个顶点在数组中的下标
        self.VertexOne = None
        self.VertexTwo = None
        # 与VertexOne对应的顶点相连的下一条边NextEdgeOne
        self.NextEdgeOne = None
        # 与VertexTwo对应的顶点相连的下一条边NextEdgeTwo
        self.NextEdgeTwo = None
        self.info = None

多重邻接表表示的图定义如下：

class GraphAdjacencyMultitable(object):
    """
    无向图的邻接多重表
    """
    def __init__(self):
        self.vertices = []
        self.vertexnum = 0
        self.edgenum = 0

无向图及其邻接多重链表：

到此这篇关于P-ython数据结构之图的存储结构详解的文章就介绍到这了,更多相关P-ython图的存储结构内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！