python机器学习之神经网络（二）

由于Rosenblatt感知器的局限性，对于非线性分类的效果不理想。为了对线性分类无法区分的数据进行分类，需要构建多层感知器结构对数据进行分类，多层感知器结构如下：

该网络由输入层，隐藏层，和输出层构成，能表示种类繁多的非线性曲面，每一个隐藏层都有一个激活函数，将该单元的输入数据与权值相乘后得到的值(即诱导局部域)经过激活函数，激活函数的输出值作为该单元的输出，激活函数类似与硬限幅函数，但硬限幅函数在阈值处是不可导的，而激活函数处处可导。本次程序中使用的激活函数是tanh函数，公式如下：

tanh函数的图像如下：

程序中具体的tanh函数形式如下：

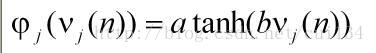
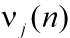就是神经元j的诱导局部域

它的局部梯度分两种情况：

(1)神经元j没有位于隐藏层：

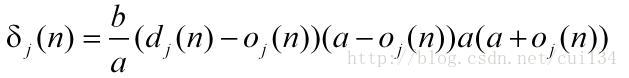
(2)神经元j位于隐藏层：

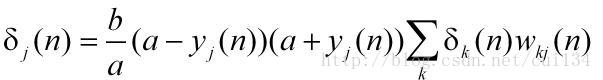
其中k是单元j后面相连的所有的单元。

局部梯度得到之后，根据增量梯度下降法的权值更新法则

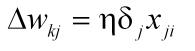
即可得到下一次的权值w，经过若干次迭代，设定误差条件，即可找到权值空间的最小值。

python程序如下，为了能够可视化，训练数据采用二维数据，每一个隐藏层有8个节点，设置了7个隐藏层，一个输出层，输出层有2个单元：

import numpy as np
import random
import copy
import matplotlib.pyplot as plt 

#x和d样本初始化
train_x = [[1,6],[3,12],[3,9],[3,21],[2,16],[3,15]]
d =[[1,0],[1,0],[0,1],[0,1],[1,0],[0,1]]
warray_txn=len(train_x[0])
warray_n=warray_txn*4 

#基本参数初始化
oldmse=10**100
fh=1
maxtrycount=500
mycount=0.0
if maxtrycount>=20:
    r=maxtrycount/5
else:
    r=maxtrycount/2
#sigmoid函数
ann_sigfun=None
ann_delta_sigfun=None
#总层数初始化，比非线性导数多一层线性层
alllevel_count=warray_txn*4
# 非线性层数初始化
hidelevel_count=alllevel_count-1 

#学习率参数
learn_r0=0.002
learn_r=learn_r0
#动量参数
train_a0=learn_r0*1.2
train_a=train_a0
expect_e=0.05
#对输入数据进行预处理
ann_max=[]
for m_ani in xrange(0,warray_txn):       #找出训练数据中每一项的最大值
  temp_x=np.array(train_x)
  ann_max.append(np.max(temp_x[:,m_ani]))
ann_max=np.array(ann_max) 

def getnowsx(mysx,in_w):
    '''''生成本次的扩维输入数据 '''
    '''''mysx==>输入数据，in_w==>权值矩阵，每一列为一个神经元的权值向量'''
    global warray_n
    mysx=np.array(mysx)
    x_end=[]
    for i in xrange(0,warray_n):
        x_end.append(np.dot(mysx,in_w[:,i]))
    return x_end 

def get_inlw(my_train_max,w_count,myin_x):
    '''''找出权值矩阵均值接近0，输出结果方差接近1的权值矩阵'''
    #对随机生成的多个权值进行优化选择，选择最优的权值
    global warray_txn
    global warray_n
    mylw=[]
    y_in=[]
    #生成测试权值
    mylw=np.random.rand(w_count,warray_txn,warray_n)
    for ii in xrange (0,warray_txn):
      mylw[:,ii,:]=mylw[:,ii,:]*1/float(my_train_max[ii])-1/float(my_train_max[ii])*0.5 

    #计算输出
    for i in xrange(0,w_count):
        y_in.append([])
        for xj in xrange(0,len(myin_x)):
            y_in[i].append(getnowsx(myin_x[xj],mylw[i]))
    #计算均方差
    mymin=10**5
    mychoice=0
    for i in xrange(0,w_count):
        myvar=np.var(y_in[i])
        if abs(myvar-1)<mymin:
            mymin=abs(myvar-1)
            mychoice=i
    #返回数据整理的权值矩阵
    return mylw[mychoice]
mylnww=get_inlw(ann_max,300,train_x) 

def get_inputx(mytrain_x,myin_w):
    '''''将训练数据经过权值矩阵，形成扩维数据'''
    end_trainx=[]
    for i in xrange(0,len(mytrain_x)):
        end_trainx.append(getnowsx(mytrain_x[i],myin_w))
    return end_trainx 

x=get_inputx(train_x,mylnww)#用于输入的扩维数据
#对测试数据进行扩维
def get_siminx(sim_x):
    global mylnww
    myxx=np.array(sim_x)
    return get_inputx(myxx,mylnww)
#计算一层的初始化权值矩阵
def getlevelw(myin_x,wo_n,wi_n,w_count):
    mylw=[]
    y_in=[]
    #生成测试权值
    mylw=np.random.rand(w_count,wi_n,wo_n)
    mylw=mylw*2.-1 

    #计算输出
    for i in xrange(0,w_count):
        y_in.append([])
        for xj in xrange(0,len(myin_x)):
          x_end=[]
          for myii in xrange(0,wo_n):
            x_end.append(np.dot(myin_x[xj],mylw[i,:,myii]))
          y_in[i].append(x_end)
    #计算均方差
    mymin=10**3
    mychoice=0
    for i in xrange(0,w_count):
        myvar=np.var(y_in[i])
        if abs(myvar-1)<mymin:
            mymin=abs(myvar-1)
            mychoice=i
    #返回数据整理的权值矩阵
    csmylw=mylw[mychoice]
    return csmylw,y_in[mychoice]
ann_w=[]
def init_annw():
  global x
  global hidelevel_count
  global warray_n
  global d
  global ann_w
  ann_w=[] 

  lwyii=np.array(x)
  #初始化每层的w矩阵
  for myn in xrange(0,hidelevel_count):
    #层数
    ann_w.append([])
    if myn==hidelevel_count-1:
      for iii in xrange(0,warray_n):
        ann_w[myn].append([])
        for jjj in xrange(0,warray_n):
                ann_w[myn][iii].append(0.0)
    elif myn==hidelevel_count-2:
      templw,lwyii=getlevelw(lwyii,len(d[0]),warray_n,200)
      for xii in xrange(0,warray_n):
        ann_w[myn].append([])
        for xjj in xrange(0,len(d[0])):
          ann_w[myn][xii].append(templw[xii,xjj])
        for xjj in xrange(len(d[0]),warray_n):
          ann_w[myn][xii].append(0.0)
    else:
      templw,lwyii=getlevelw(lwyii,warray_n,warray_n,200)
      for xii in xrange(0,warray_n):
        ann_w[myn].append([])
        for xjj in xrange(0,warray_n):
          ann_w[myn][xii].append(templw[xii,xjj])
  ann_w=np.array(ann_w) 

def generate_lw(trycount):
  global ann_w
  print u"产生权值初始矩阵",
  meanmin=1
  myann_w=ann_w
  alltry=30
  tryc=0
  while tryc<alltry:
    for i_i in range(trycount):
      print ".",
      init_annw()
      if abs(np.mean(np.array(ann_w)))<meanmin:
        meanmin=abs(np.mean(np.array(ann_w)))
        myann_w=ann_w
    tryc+=1
    if abs(np.mean(np.array(myann_w)))<0.008:break 

  ann_w=myann_w
  print
  print u"权值矩阵平均:%f"%(np.mean(np.array(ann_w)))
  print u"权值矩阵方差:%f"%(np.var(np.array(ann_w)))
generate_lw(15) 

#前次训练的权值矩阵
ann_oldw=copy.deepcopy(ann_w)
#梯度初始化
#输入层即第一层隐藏层不需要，所以第一层的空间无用
ann_delta=[]
for i in xrange(0,hidelevel_count):
    ann_delta.append([])
    for j in xrange(0,warray_n):
        ann_delta[i].append(0.0)
ann_delta=np.array(ann_delta) 

#输出矩阵yi初始化
ann_yi=[]
for i in xrange(0,alllevel_count):
    #第一维是层数，从0开始
    ann_yi.append([])
    for j in xrange(0,warray_n):
        #第二维是神经元
        ann_yi[i].append(0.0)
ann_yi=np.array(ann_yi)    

#输出层函数
def o_func(myy):
    myresult=[]
    mymean=np.mean(myy)
    for i in xrange(0,len(myy)):
        if myy[i]>=mymean:
            myresult.append(1.0)
        else:
            myresult.append(0.0)
    return np.array(myresult) 

def get_e(myd,myo):
    return np.array(myd-myo)
def ann_atanh(myv):
    atanh_a=1.7159#>0
    atanh_b=2/float(3)#>0
    temp_rs=atanh_a*np.tanh(atanh_b*myv)
    return temp_rs
def ann_delta_atanh(myy,myd,nowlevel,level,n,mydelta,myw):
  anndelta=[]
  atanh_a=1.7159#>0
  atanh_b=2/float(3)#>0
  if nowlevel==level:
    #输出层
    anndelta=(float(atanh_b)/atanh_a)*(myd-myy)*(atanh_a-myy)*(atanh_a+myy)
  else:
    #隐藏层
    anndelta=(float(atanh_b)/atanh_a)*(atanh_a-myy)*(atanh_a+myy)
    temp_rs=[]
    for j in xrange(0,n):
        temp_rs.append(sum(myw[j]*mydelta))
    anndelta=anndelta*temp_rs
  return anndelta 

def sample_train(myx,myd,n,sigmoid_func,delta_sigfun):
    '''''一个样本的前向和后向计算'''
    global ann_yi
    global ann_delta
    global ann_w
    global ann_wj0
    global ann_y0
    global hidelevel_count
    global alllevel_count
    global learn_r
    global train_a
    global ann_oldw
    level=hidelevel_count
    allevel=alllevel_count 

    #清空yi输出信号数组
    hidelevel=hidelevel_count
    alllevel=alllevel_count
    for i in xrange(0,alllevel):
        #第一维是层数，从0开始
        for j in xrange(0,n):
            #第二维是神经元
            ann_yi[i][j]=0.0
    ann_yi=np.array(ann_yi)
    yi=ann_yi 

    #清空delta矩阵
    for i in xrange(0,hidelevel-1):
        for j in xrange(0,n):
            ann_delta[i][j]=0.0
    delta=ann_delta
    #保留W的拷贝，以便下一次迭代
    ann_oldw=copy.deepcopy(ann_w)
    oldw=ann_oldw
    #前向计算 

    #对输入变量进行预处理
    myo=np.array([])
    for nowlevel in xrange(0,alllevel):
        #一层层向前计算
        #计算诱导局部域
        my_y=[]
        myy=yi[nowlevel-1]
        myw=ann_w[nowlevel-1]
        if nowlevel==0:
            #第一层隐藏层
            my_y=myx
            yi[nowlevel]=my_y
        elif nowlevel==(alllevel-1):
            #输出层
            my_y=o_func(yi[nowlevel-1,:len(myd)])
            yi[nowlevel,:len(myd)]=my_y
        elif nowlevel==(hidelevel-1):
            #最后一层输出层
            for i in xrange(0,len(myd)):
                temp_y=sigmoid_func(np.dot(myw[:,i],myy))
                my_y.append(temp_y)
            yi[nowlevel,:len(myd)]=my_y
        else:
            #中间隐藏层
            for i in xrange(0,len(myy)):
                temp_y=sigmoid_func(np.dot(myw[:,i],myy))
                my_y.append(temp_y)
            yi[nowlevel]=my_y 

    #计算误差与均方误差
    myo=yi[hidelevel-1][:len(myd)]
    myo_end=yi[alllevel-1][:len(myd)]
    mymse=get_e(myd,myo_end) 

    #反向计算
    #输入层不需要计算delta,输出层不需要计算W 

    #计算delta
    for nowlevel in xrange(level-1,0,-1):
        if nowlevel==level-1:
            mydelta=delta[nowlevel]
            my_n=len(myd)
        else:
            mydelta=delta[nowlevel+1]
            my_n=n
        myw=ann_w[nowlevel]
        if nowlevel==level-1:
            #输出层
            mydelta=delta_sigfun(myo,myd,None,None,None,None,None)
##            mydelta=mymse*myo
        elif nowlevel==level-2:
            #输出隐藏层的前一层，因为输出结果和前一层隐藏层的神经元数目可能存在不一致
            #所以单独处理，传相当于输出隐藏层的神经元数目的数据
            mydelta=delta_sigfun(yi[nowlevel],myd,nowlevel,level-1,my_n,mydelta[:len(myd)],myw[:,:len(myd)])
        else:
            mydelta=delta_sigfun(yi[nowlevel],myd,nowlevel,level-1,my_n,mydelta,myw) 

        delta[nowlevel][:my_n]=mydelta
    #计算与更新权值W
    for nowlevel in xrange(level-1,0,-1):
        #每个层的权值不一样
        if nowlevel==level-1:
            #输出层
            my_n=len(myd)
            mylearn_r=learn_r*0.8
            mytrain_a=train_a*1.6
        elif nowlevel==1:
            #输入层
            my_n=len(myd)
            mylearn_r=learn_r*0.9
            mytrain_a=train_a*0.8
        else:
            #其它层
            my_n=n
            mylearn_r=learn_r
            mytrain_a=train_a 

        pre_level_myy=yi[nowlevel-1]
        pretrain_myww=oldw[nowlevel-1]
        pretrain_myw=pretrain_myww[:,:my_n] 

        #第二个调整参数
        temp_i=[]         

        for i in xrange(0,n):
            temp_i.append([])
            for jj in xrange(0,my_n):
                temp_i[i].append(mylearn_r*delta[nowlevel,jj]*pre_level_myy[i])
        temp_rs2=np.array(temp_i)
        temp_rs1=mytrain_a*pretrain_myw
        #总调整参数
        temp_change=temp_rs1+temp_rs2
        my_ww=ann_w[nowlevel-1]
        my_ww[:,:my_n]+=temp_change 

    return mymse 

def train_update(level,nowtraincount,sigmoid_func,delta_sigfun):
    '''''一次读取所有样本，然后迭代一次进行训练'''
    #打乱样本顺序
    global learn_r
    global train_a
    global train_a0
    global learn_r0
    global r
    global x
    global d
    global maxtrycount
    global oldmse
    x_n=len(x)
    ids=range(0,x_n)
    train_ids=[]
    sample_x=[]
    sample_d=[] 

    while len(ids)>0:
        myxz=random.randint(0,len(ids)-1)
        train_ids.append(ids[myxz])
        del ids[myxz] 

    for i in xrange(0,len(train_ids)):
        sample_x.append(x[train_ids[i]])
        sample_d.append(d[train_ids[i]])
    sample_x=np.array(sample_x)
    sample_d=np.array(sample_d) 

    #读入x的每个样本，进行训练
    totalmse=0.0
    mymse=float(10**-10)
    for i in xrange(0,x_n): 

        mymse=sample_train(sample_x[i],sample_d[i],warray_n,sigmoid_func,delta_sigfun)
        totalmse+=sum(mymse*mymse)
    totalmse=np.sqrt(totalmse/float(x_n))
    print u"误差为：%f" %(totalmse)
    nowtraincount[0]+=1
    learn_r=learn_r0/(1+float(nowtraincount[0])/r)
    train_a=train_a0/(1+float(nowtraincount[0])/r)
    if nowtraincount[0]>=maxtrycount:
        return False,True,totalmse
    elif totalmse<expect_e:
    #(totalmse-oldmse)/oldmse>0.1 and (totalmse-oldmse)/oldmse<1:
        print u"训练成功，正在进行检验"
        totalmse=0.0
        for i in xrange(0,x_n):
            mytemper=(sample_d[i]-simulate(sample_x[i],sigmoid_func,delta_sigfun))
            totalmse+=sum(mytemper*mytemper)
        totalmse=np.sqrt(totalmse/float(x_n))
        if totalmse<expect_e:
            return False,False,totalmse
    oldmse=totalmse
    return True,False,totalmse 

def train():
    '''''训练样本，多次迭代'''
    global hidelevel_count
    nowtraincount=[]
    nowtraincount.append(0)
    #sigmoid函数指定
    delta_sigfun=ann_delta_atanh
    sigmoid_func=ann_atanh 

    tryerr=0
    while True:
        print u"-------开始第%d次训练---------"%(nowtraincount[0]+1),
        iscontinue,iscountout,mymse=train_update(hidelevel_count,nowtraincount,sigmoid_func,delta_sigfun)
        if not iscontinue:
            if iscountout :
                print u"训练次数已到,误差为：%f"%mymse
                tryerr+=1
                if tryerr>3:
                  break
                else:
                  print u"训练失败，重新尝试第%d次"%tryerr
                  nowtraincount[0]=0
                  generate_lw(15+tryerr*2)
            else:
                print u"训练成功,误差为：%f"%mymse
                break 

def simulate(myx,sigmoid_func,delta_sigfun):
    '''''一个样本的仿真计算'''
    print u"仿真计算中"
    global ann_yi
    global ann_w
    global ann_wj0
    global ann_y0
    global hidelevel_count
    global alllevel_count
    global d
    myd=d[0] 

    myx=np.array(myx)
    n=len(myx) 

    level=hidelevel_count
    allevel=alllevel_count 

    #清空yi输出信号数组
    hidelevel=hidelevel_count
    alllevel=alllevel_count
    for i in xrange(0,alllevel):
        #第一维是层数，从0开始
        for j in xrange(0,n):
            #第二维是神经元
            ann_yi[i][j]=0.0
    ann_yi=np.array(ann_yi)
    yi=ann_yi 

    #前向计算
    myo=np.array([])
    myy=np.array([])
    for nowlevel in xrange(0,alllevel):
        #一层层向前计算
        #计算诱导局部域
        my_y=[]
        myy=yi[nowlevel-1]
        myw=ann_w[nowlevel-1]
        if nowlevel==0:
            #第一层隐藏层
            my_y=myx
            yi[nowlevel]=my_y
        elif nowlevel==(alllevel-1):
            #线性输出层，使用线性激活
            my_y=o_func(yi[nowlevel-1,:len(myd)])
            yi[nowlevel,:len(myd)]=my_y
        elif nowlevel==(hidelevel-1):
            #最后一层隐藏输出层，使用线性激活
            for i in xrange(0,len(myd)):
                temp_y=sigmoid_func(np.dot(myw[:,i],myy))
                my_y.append(temp_y)
            yi[nowlevel,:len(myd)]=my_y
        else:
            #中间隐藏层
            #中间隐藏层需要加上偏置
            for i in xrange(0,len(myy)):
                temp_y=sigmoid_func(np.dot(myw[:,i],myy))
                my_y.append(temp_y)
            yi[nowlevel]=my_y 

    return yi[alllevel-1,:len(myd)]
train() 

delta_sigfun=ann_delta_atanh
sigmoid_func=ann_atanh 

for xn in xrange(0,len(x)):
    if simulate(x[xn],sigmoid_func,delta_sigfun)[0]>0:
        plt.plot(train_x[xn][0],train_x[xn][1],"bo")
    else:
        plt.plot(train_x[xn][0],train_x[xn][1],"b*") 

temp_x=np.random.rand(20)*10
temp_y=np.random.rand(20)*20+temp_x
myx=temp_x
myy=temp_y
plt.subplot(111)
x_max=np.max(myx)+5
x_min=np.min(myx)-5
y_max=np.max(myy)+5
y_min=np.min(myy)-5
plt.xlim(x_min,x_max)
plt.ylim(y_min,y_max)
for i in xrange(0,len(myx)):
    test=get_siminx([[myx[i],myy[i]]])
    if simulate(test,sigmoid_func,delta_sigfun)[0]>0:
        plt.plot(myx[i],myy[i],"ro")
    else:
        plt.plot(myx[i],myy[i],"r*")  

plt.show() 

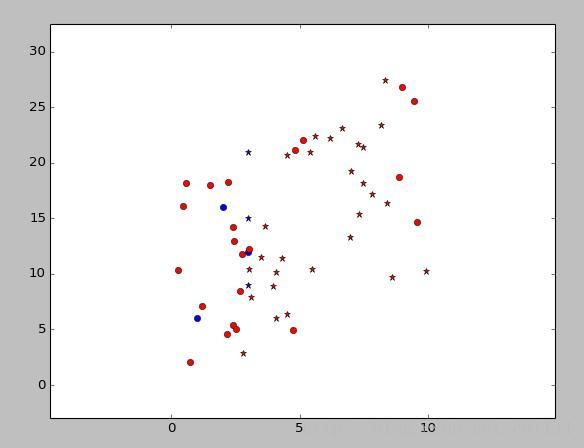
图中蓝色是训练数据，红色是测试数据，圈圈代表类型[1,0]，星星代表类型[0,1]。

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。