python实现基于朴素贝叶斯的垃圾分类算法

一、模型方法

本工程采用的模型方法为朴素贝叶斯分类算法，它的核心算法思想基于概率论。我们称之为“朴素”，是因为整个形式化过程只做最原始、最简单的假设。朴素贝叶斯是贝叶斯决策理论的一部分，所以讲述朴素贝叶斯之前有必要快速了解一下贝叶斯决策理论。假设现在我们有一个数据集，它由两类数据组成，数据分布如下图所示。

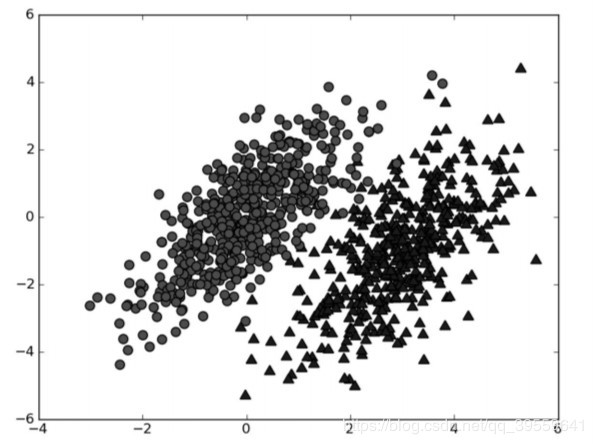
我们现在用p1(x,y)表示数据点(x,y)属于类别1（图中用圆点表示的类别）的概率，用p2(x,y)表示数据点(x,y)属于类别2（图中用三角形表示的类别）的概率，那么对于一个新数据点(x,y)，可以用下面的规则来判断它的类别：

如果 p1(x,y) > p2(x,y)，那么类别为1。

如果 p2(x,y) > p1(x,y)，那么类别为2。

也就是说，我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想，即选择具有最高概率的决策。

在本工程中我们可以使用条件概率来进行分类。其条件概率公式如下：

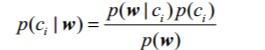
其中粗体w表示这是一个向量，它是有多个值组成。对于类别i表示分类的个数，在本工程中i=0时，c0表示非垃圾邮件。i=1时，c1表示垃圾邮件。w展开为一个个独立特征，那么就可以将上述概率写作p(w0,w1,w2..wN|ci)。这里假设所有词都互相独立，该假设也称作条件独立性假设，它意味着可以使用p(w0|ci)p(w1|ci)p(w2|ci)...p(wN|ci)来计算上述概率，这就极大地简化了计算的过程，这也是被称为朴素贝叶斯的原因。在本工程中wj代表第i个单词特征，而p(wj|ci)则代表了在垃圾邮件（或非垃圾邮件）中，第j个单词出现的概率；而p(w|ci)则表示在垃圾邮件（或非垃圾邮件）中的全体向量特征（单词向量特征）出现的概率；而p(ci| w)则表示在全体向量特征（单词向量特征）下是垃圾邮件（或非垃圾邮件）的概率。本工程项目主要是计算p(ci|w)；p(ci)则表示是垃圾邮件（或非垃圾邮件）的概率。

二、系统设计

数据的收集及保存

邮件的收集来源于网上，保存在email文件夹中。其中email分两个子文件，一个为ham文件夹（保存非垃圾邮件），另一个为spam文件夹（保存垃圾邮件）。ham与spam中各保存25各邮件，保存格式为x.txt(x为1到25)。

训练集和测试集的选取

由于收集的邮件个数有限，故选取80%的邮件作为训练集，其方式为随机选取。剩余20%邮件作为测试集。

特征向量构建

特征向量的构建分为两种，一个为对训练集的特征向量构建。一个为测试集的特征向量构建。对于训练集特征向量只需要分为两类，因为邮件只分为垃圾邮件和非垃圾邮件。特征向量分为对训练集中所有垃圾邮件中构成的特征向量（记做w）和训练集中所有非垃圾邮件构成特征向量（记做w'）。对于w的计算实际就是统计所有训练集中垃圾邮件中的每个单词的出现情况，出现则次数加1。其计数初值为1，按照正常情况应为0，因为用的朴素贝叶斯算法，假设所有词都互相独立 ，就有p(w|ci) = p(w0|ci)p(w1|ci)p(w2|ci)...p(wN|ci)。所以当第i个单词wi在其特征向量中没有出现，则有p(wi|ci) =0,这就导致了p(w|ci)导致结果的不正确性。所以我们索性将所有单词默认出现1遍，所以从1开始计数。对于w'的计算和w的计算方法相同，这里就不在赘述。

对于测试集的特征向量构建就是对每个邮件中单词出现的次数进行统计，其单词表可以来源于50个邮件中的所有单词。对于每一个邮件中单词如果出现就加1，其计数初值为0。每个测试集的邮件都需构建特征向量。其特征向量在python中可用列表表示。

构建贝叶斯分类器

对于分类器的训练其目的训练三个参数为p1Vect(w中每个单词出现的概率构成的特征向量)、p0Vect(w'中每个单词出现的概率构成的特征向量)和pAbusive(训练集中垃圾邮件的概率)。对于p1Vect、p0Vect计算可能会造成下溢出，这 是 由 于 太 多 很 小 的 数 相 乘 造 成 的 。 当 计 算 乘 积p(w0|ci)p(w1|ci)p(w2|ci)...p(wN|ci)时，由于大部分因子都非常小，所以程序会下溢出或者得到不正确的答案。一种解决办法是对乘积取自然对数。在代数中有ln(a*b) = ln(a)+ln(b)，于是通过求对数可以避免下溢出或者浮点数舍入导致的错误。同时，采用自然对数进行处理不会有任何损失。图1给出函数f(x)与ln(f(x))的曲线。检查这两条曲线，就会发现它们在相同区域内同时增加或者减少，并且在相同点上取到极值。它们的取值虽然不同，但不影响最终结果。

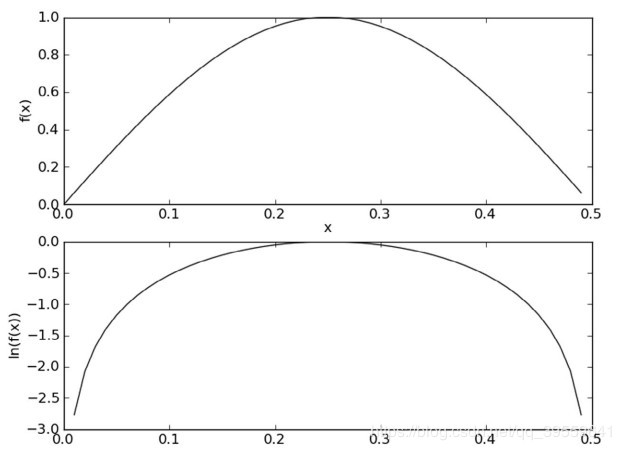
所以p1Vect = log(w/p1Denom)，p0Vect = log(w'/p0Denom)，其中p1Denom、p0Denom分别为垃圾邮件中单词的总数和非垃圾邮件中单词的总数。而pAbusive 就等于训练集中垃圾邮件总数与训练集中邮件总数之比。

测试集验证与评估

对于判断是否为垃圾邮件，只需对每个邮件判断p(c0|w)(不是垃圾邮件的概率)与p(c1|w)（是垃圾邮件的概率）。

q如果p(c0|w) > p(c1|w)，那么该邮件为非垃圾邮件。

q如果 p(c0|w) < p(c1|w)，那么该邮件为垃圾邮件。

然而p(ci|w)(i=0或1)的计算则依赖于p(w|ci)与p(ci)的计算，p(w)无需计算。所以最终结果依赖于pi = p(w|ci)·p(ci)。由于p(w|ci)很小，可能向下溢出。所以我们取以10为底的对数得log(pi) = log(p(w|ci))+log(p(ci)),所以可得以下结论：

q如果log(p0) > log(p1)，那么该邮件为非垃圾邮件。

q如果log(p0) < log(p1)，那么该邮件为垃圾邮件。

其中p(w|ci)为在垃圾邮件（或非垃圾邮件）中的全体向量特征（单词向量特征）出现的概率，p(ci)为训练集中垃圾邮件（或非垃圾邮件）的概率。

三、系统演示与实验结果分析对比

由训练集（40个）和测试集（个）的样本数目比较小，所以测试的分类结果正确性为90%-100%之间，如下图所示：

本工程只是对邮件进行二分类，贝叶斯算法也可以处理多分类问题，如新闻的分类，如分成军事、体育、科技等等。当然本工程只是对英文的垃圾邮件分类，但也可以对中文的垃圾邮件分类（可用python中的jieba的库模块进行对中文分词）。

四、代码实现

#coding=UTF-8
import random
from numpy import *

#解析英文文本，并返回列表
def textParse(bigString):
 #将单词以空格划分
 listOfTokens = bigString.split()
 #去除单词长度小于2的无用单词
 return [tok.lower() for tok in listOfTokens if len(tok)>2]

#去列表中重复元素，并以列表形式返回
def createVocaList(dataSet):
 vocabSet = set({})
 #去重复元素，取并集
 for document in dataSet:
 vocabSet = vocabSet | set(document)
 return list(vocabSet)

#统计每一文档（或邮件）在单词表中出现的次数，并以列表形式返回
def setOfWordsToVec(vocabList,inputSet):
 #创建0向量，其长度为单词量的总数
 returnVec = [0]*len(vocabList)
 #统计相应的词汇出现的数量
 for word in inputSet:
 if word in vocabList:
  returnVec[vocabList.index(word)] += 1
 return returnVec

#朴素贝叶斯分类器训练函数
def trainNB0(trainMatrix,trainCategory):
 #获取训练文档数
 numTrainDocs = len(trainMatrix)
 #获取每一行词汇的数量
 numWords = len(trainMatrix[0])
 #侮辱性概率(计算p(Ci))，计算垃圾邮件的比率
 pAbusive = sum(trainCategory)/float(numTrainDocs)
 #统计非垃圾邮件中各单词在词数列表中出现的总数（向量形式）
 p0Num = ones(numWords)
 #统计垃圾邮件中各单词在词数列表中出现的总数（向量形式）
 p1Num = ones(numWords)
 #统计非垃圾邮件总单词的总数（数值形式）
 p0Denom = 2.0
 #统计垃圾邮件总单词的总数（数值形式）
 p1Denom = 2.0
 for i in range(numTrainDocs):
 #如果是垃圾邮件
 if trainCategory[i] == 1:
  p1Num += trainMatrix[i]
  p1Denom +=sum(trainMatrix[i])
 #如果是非垃圾邮件
 else:
  p0Num += trainMatrix[i]
  p0Denom +=sum(trainMatrix[i])
 #计算每个单词在垃圾邮件出现的概率（向量形式）
 p1Vect = log(p1Num/p1Denom)
 #计算每个单词在非垃圾邮件出现的概率（向量形式）
 p0Vect = log(p0Num/p0Denom)
 return p0Vect,p1Vect,pAbusive
#朴素贝叶斯分类函数
def classifyNB(vec2Classify,p0Vec,p1Vec,pClass1):
 p1 = sum(vec2Classify*p1Vec)+log(pClass1)
 p0 = sum(vec2Classify*p0Vec)+log(1.0 - pClass1)
 if p1 > p0:
 return 1
 else :
 return 0
#test
def spamtest():
 #导入并解析文本文件
 docList =[];classList=[];fullText = []
 for i in range(1,26):
 #读取第i篇垃圾文件，并以列表形式返回
 wordList = textParse(open('email/spam/{0}.txt'.format(i)).read())
 #转化成二维列表
 docList.append(wordList)
 #一维列表进行追加
 fullText.extend(wordList)
 #标记文档为垃圾文档
 classList.append(1)
 #读取第i篇非垃圾文件，并以列表形式返回
 wordList = textParse(open('email/ham/{0}.txt'.format(i)).read())
 #转化成二维列表
 docList.append(wordList)
 #一维列表进行追加
 fullText.extend(wordList)
 #标记文档为非垃圾文档
 classList.append(0)
 #去除重复的单词元素
 vocabList = createVocaList(docList)
 #训练集，选40篇doc
 trainingSet = [x for x in range(50)]
 #测试集，选10篇doc
 testSet = []
 #选出10篇doc作测试集
 for i in range(10):
 randIndex = int(random.uniform(0,len(trainingSet)))
 testSet.append(trainingSet[randIndex])
 del trainingSet[randIndex]
 trainMat = [];trainClasses=[]
 #选出40篇doc作训练集
 for docIndex in trainingSet:
 trainMat.append(setOfWordsToVec(vocabList, docList[docIndex]))
 trainClasses.append(classList[docIndex])
 p0V,p1V,pSpam = trainNB0(array(trainMat), array(trainClasses))
 #对测试集分类
 errorCount = 0
 for docIndex in testSet:
 wordVector = setOfWordsToVec(vocabList,docList[docIndex])
 if classifyNB(array(wordVector), p0V, p1V, pSpam)!=classList[docIndex]:
  errorCount+=1
 print("错误率为：{0}".format(float(errorCount)/len(testSet)))
spamtest()

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。