浅谈线性表的原理及简单实现方法

一、线性表

原理：零个或多个同类数据元素的有限序列

原理图：

特点 ：

1、有序性

2、有限性

3、同类型元素

4、第一个元素无前驱，最后一个元素无后继，中间的元素有一个前驱并且有一个后继

线性表是一种逻辑上的数据结构，在物理上一般有两种实现 顺序实现和链表实现

二、基于数组的 线性表顺序实现

原理 ： 用一段地址连续的存储单元依次存储线性表数据元素。

原理图：

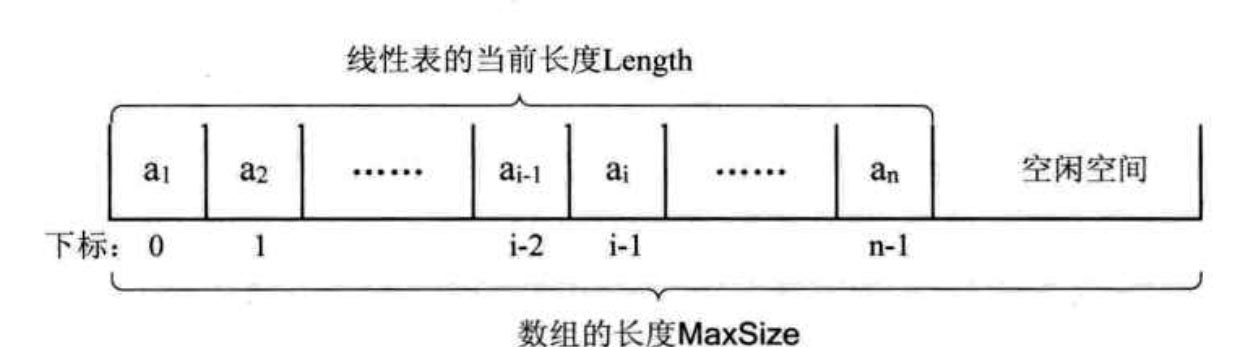
算法原理：

1、初始化一个定长的数组空间 elementData[] , size 存储长度 存储元素

2、通过索引来快速存取元素

3、通过数组复制实现元素的插入和删除

总结：

1、无需为表示表中元素之间的逻辑关系增加额外的存储空间

2、可以快速存取表中任一位置元素

3、插入和删除需要进行数组复制（即大量元素的移动）

4、线性表长度变化较大时，需要频繁扩容，并造成存储空间碎片

实现代码：

接口定义：

package online.jfree.base;

/**
 * author : Guo LiXiao
 * date : 2017-6-14 11:46
 */

public interface LineList <E>{

 /**
  * lineList 是否为空
  * @return
  */
 boolean isEmpty();

 /**
  * 清空 lineList
  */
 void clear();

 /**
  * 获取指定位置元素
  * @param index
  * @return
  */
 E get(int index);

 /**
  * 获取元素第一次出现的位置
  * @param e
  * @return
  */
 int indexOf(E e);

 /**
  * 判断 lineList是否包含指定元素
  * @param e
  * @return
  */
 boolean contains(E e);

 /**
  * 设置指定位置数据，如数据已存在 则覆盖原数据
  * @param index
  * @param e
  * @return
  */
 E set(int index, E e);

 /**
  * 移除指定位置元素
  * @param index
  * @return
  */
 E remove(int index);

 /**
  * 在lineList结尾插入元素
  * @param e
  * @return
  */
 E add(E e);

 /**
  * 在index后面插入元素
  * @param index
  * @param e
  * @return
  */
 E add(int index, E e);

 /**
  * 返回lineList长度
  * @return
  */
 int size();

}

算法实现：

package online.jfree.base;

/**
 * author : Guo LiXiao
 * date : 2017-6-15 13:44
 */

public class OrderedLineList<E> implements LineList<E> {

 private static final int INIT_CAPACITY = 10;

 private transient E[] elementData;

 private transient int elementLength;

 private int size;

 public OrderedLineList() {
  this(0);
 }

 public OrderedLineList(int initCapacity) {
  init(initCapacity);
 }

 private void init(int initCapacity) {
  if (initCapacity >= 0) {
   this.elementData = (E[]) new Object[initCapacity];
   this.elementLength = initCapacity;
  } else {
   throw new IllegalArgumentException("Illegal Capacity: " +
     initCapacity);
  }
  this.size = 0;
 }

 /**
  * 扩容
  */
 private void dilatation() {
  int oldCapacity = this.elementLength;
  int newCapacity = oldCapacity;
  if (oldCapacity <= this.size) {
   newCapacity = oldCapacity + INIT_CAPACITY;
  }else if(oldCapacity - INIT_CAPACITY > this.size){
   newCapacity = oldCapacity - INIT_CAPACITY;
  }
  if (oldCapacity != newCapacity){
   E[] newElementData = (E[]) new Object[newCapacity];
   System.arraycopy(elementData, 0, newElementData, 0, oldCapacity);
   this.elementLength = newCapacity;
   this.elementData = newElementData;
  }
 }

 /**
  * 校验列表索引越界
  * @param index
  */
 private void checkCapacity(int index){
  if (index > this.size - 1 || index < 0)
   throw new IndexOutOfBoundsException(new StringBuffer("[index : ").append(index).append("] , [size : ").append(size).append("] ").toString());
 }

 @Override
 public boolean isEmpty() {
  return this.size == 0;
 }

 @Override
 public void clear() {
  this.init(0);
 }

 @Override
 public E get(int index) {
  this.checkCapacity(index);
  return this.elementData[index];
 }

 @Override
 public int indexOf(E e) {
  for (int i = 0; i < this.size; i++){
   if (e == null && elementData[i] == null || e.equals(elementData[i])){
    return i;
   }
  }
  return -1;
 }

 @Override
 public boolean contains(E e) {
  return this.indexOf(e) > 0;
 }

 @Override
 public E set(int index, E e) {
  this.checkCapacity(index);
  this.dilatation();
  E oldElement = this.elementData[index];
  this.elementData[index] = e;
  return oldElement;
 }

 @Override
 public E remove(int index) {
  this.dilatation();
  E e = elementData[index];
  if (index == size - 1) elementData[index] = null;
  else {
   int length = size - index - 1;
   System.arraycopy(elementData, index + 1, elementData, index, length);
  }
  size --;
  return e;
 }

 @Override
 public E add(E e) {
  return this.add(size, e);
 }

 @Override
 public E add(int index, E e) {
  this.dilatation();
  if (index == size) elementData[index] = e;
  else {
   index++;
   int lastLength = size - index;
   E[] lastElementData = (E[]) new Object[lastLength];
   System.arraycopy(elementData, index, lastElementData, 0, lastLength);
   elementData[index] = e;
   System.arraycopy(lastElementData, 0, elementData, index + 1, lastLength);
  }
  size ++ ;
  return e;
 }

 @Override
 public int size() {
  return this.size;
 }

}

以上这篇浅谈线性表的原理及简单实现方法就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。