numpy稀疏矩阵的实现

目录

• 1. coo存储方式
• 2. dok_matrix
• 3. csr和csc存储方式
• 4. lil_matrix
• 5. dia_matrix
• 6. 稀疏矩阵经验

1. coo存储方式

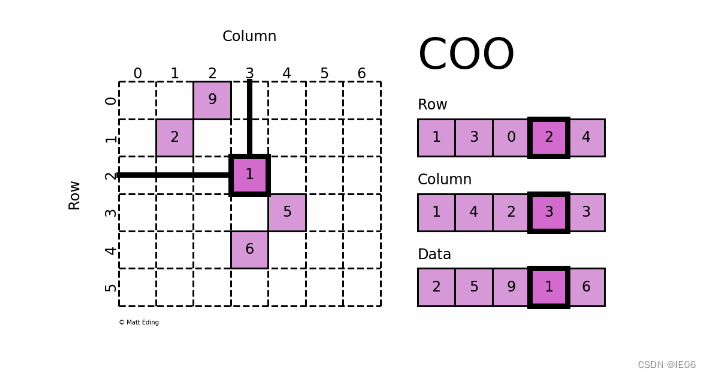
采用三元组(row, col, data)(或称为ijv format)的形式来存储矩阵中非零元素的信息。

coo_matrix的优点：有利于稀疏格式之间的快速转换（tobsr()、tocsr()、to_csc()、to_dia()、to_dok()、to_lil()；允许重复项（格式转换的时候自动相加）；能与CSR / CSC格式的快速转换

coo_matrix的缺点：不能直接进行算术运算，包括赋值

初始化方式：

coo_matrix(D), D代表密集矩阵

赋值：

>>> import numpy as np
>>> from scipy.sparse import coo_matrix

>>> _row  = np.array([0, 3, 1, 0])
>>> _col  = np.array([0, 3, 1, 2])
>>> _data = np.array([4, 5, 7, 9])
>>> coo = coo_matrix((_data, (_row, _col)), shape=(4, 4), dtype=np.int)
>>> coo.todense()  # 通过toarray方法转化成密集矩阵(numpy.matrix)
>>> coo.toarray()  # 通过toarray方法转化成密集矩阵(numpy.ndarray)
array([[4, 0, 9, 0],
       [0, 7, 0, 0],
       [0, 0, 0, 0],
       [0, 0, 0, 5]])

2. dok_matrix

​ dok_matrix，即Dictionary Of Keys based sparse matrix，是一种类似于coo matrix但又基于字典的稀疏矩阵存储方式，key由非零元素的的坐标值tuple(row, column)组成，value则代表数据值。dok matrix非常适合于增量构建稀疏矩阵，并一旦构建，就可以快速地转换为coo_matrix。

>>> import numpy as np
>>> from scipy.sparse import dok_matrix

>>> np.random.seed(10)
>>> matrix = random(3, 3, format='dok', density=0.4)
>>> matrix[1, 1] = 33
>>> matrix[2, 1] = 10
>>> matrix.toarray()
array([[ 0.        ,  0.        ,  0.        ],
       [ 0.        , 33.        ,  0.        ],
       [ 0.19806286, 10.        ,  0.22479665]])
>>> dict(matrix)
{(2, 0): 0.19806286475962398, (2, 1): 10.0, (2, 2): 0.22479664553084766, (1, 1): 33.0}

>>> isinstance(matrix, dict)
True

3. csr和csc存储方式

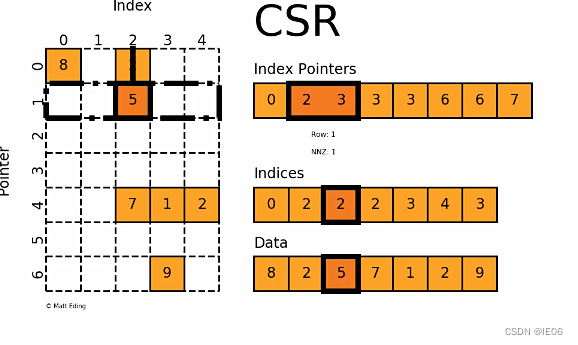
csr_matrix，全称Compressed Sparse Row matrix，即按行压缩的稀疏矩阵存储方式，由三个一维数组indptr, indices, data组成。这种格式要求矩阵元「按行顺序存储」，「每一行中的元素可以乱序存储」。那么对于每一行就只需要用一个指针表示该行元素的起始位置即可。indptr存储每一行数据元素的起始位置，indices这是存储每行中数据的列号，与data中的元素一一对应。
csr_matrix，是按列压缩，不再赘述

csr_matrix的优点：
高效的算术运算CSR + CSR，CSR * CSR等
高效的行切片
快速矩阵运算

csr_matrix的缺点：
列切片操作比较慢（考虑csc_matrix）
稀疏结构的转换比较慢（考虑lil_matrix或doc_matrix）

>>> import numpy as np
>>> from scipy.sparse import csr_matrix

>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6])
>>> csr = csr_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 2],
       [0, 0, 3],
       [4, 5, 6]])

4. lil_matrix

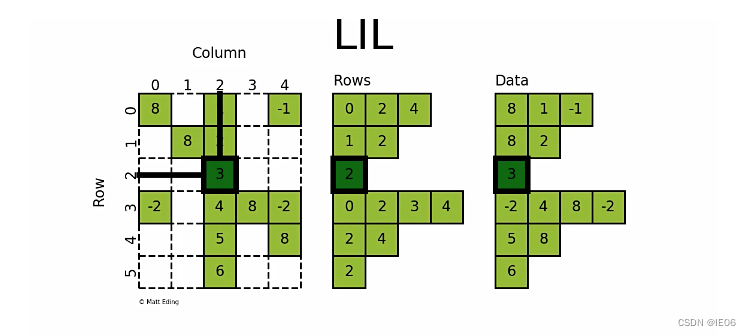
lil_matrix，即List of Lists format，又称为Row-based linked list sparse matrix。它使用两个嵌套列表存储稀疏矩阵：data保存每行中的非零元素的值，rows保存每行非零元素所在的列号(列号是顺序排序的)。
LIL matrix本身的设计是用来方便快捷构建稀疏矩阵实例，而算术运算、矩阵运算则转化成CSC、CSR格式再进行，构建大型的稀疏矩阵还是推荐使用COO格式。

5. dia_matrix

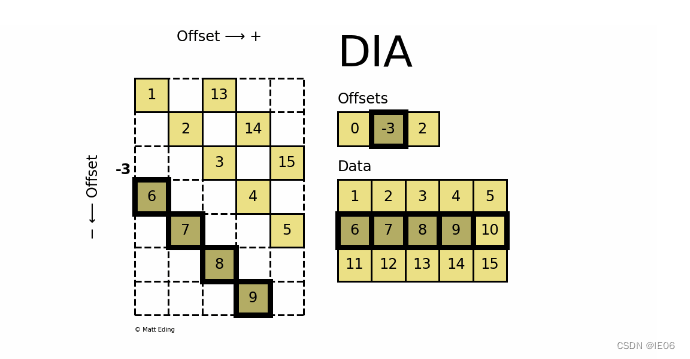
​ dia_matrix，全称Sparse matrix with DIAgonal storage，是一种对角线的存储方式。如下图中，将稀疏矩阵使用offsets和data两个矩阵来表示。

>>> data = np.arange(15).reshape(3, -1) + 1
>>> offsets = np.array([0, -3, 2])
>>> dia = sparse.dia_matrix((data, offsets), shape=(7, 5))
>>> dia.toarray()
array([[ 1,  0, 13,  0,  0],
       [ 0,  2,  0, 14,  0],
       [ 0,  0,  3,  0, 15],
       [ 6,  0,  0,  4,  0],
       [ 0,  7,  0,  0,  5],
       [ 0,  0,  8,  0,  0],
       [ 0,  0,  0,  9,  0]])

6. 稀疏矩阵经验

要有效地构造矩阵，请使用dok_matrix或lil_matrix
lil_matrix类支持基本切片和花式索引，其语法与NumPy Array类似；lil_matrix形式是基于row的，因此能够很高效的转为csr，但是转为csc效率相对较低。
要执行乘法或转置等操作，首先将矩阵转换为CSC或CSR格式，效率高
CSR格式特别适用于快速矩阵矢量产品
CSR，CSC和COO格式之间的所有转换都是线性复杂度。

到此这篇关于numpy稀疏矩阵的实现的文章就介绍到这了,更多相关numpy 稀疏矩阵内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！