C++中单链表的建立与基本操作

准备数据

准备在链表操作中需要用到的变量及数据结构

示例代码如下：


代码如下:

struct Data   //数据结点类型
{
 string key;  //关键字
 string name;
 int age;
};
struct CLType  //定义链表结构
{
 Data nodeData;
 Data *nextNode;
};

定义了链表数据元素的类型Data以及链表的数据结构CLType。结点的具体数据保存在一个结构Data中，而指针nextNode用来指向下一个结点。

我们可以认为，该链表是一个班级学生的记录，其中key表示学号，name为学生的名字，age为年龄。

追加结点

追加结点就是在链表末尾增加一个结点。表尾结点的地址部分原来保存的是空地址NULL，此时需要将其设置为新增结点的地址（即原表尾结点指向新增结点），然后将新增节点的地址部分设置为空地址NULL，即新增结点为表尾。

由于一般情况下，链表只有一个头指针head，要在末尾添加结点就需要从头指针head开始逐个检查，直到找到最后一个结点（即表尾）。

追加结点的操作步骤如下：

（1）首先分配内存地址，保存新增结点。

（2）从头指针head开始逐个检查，直到找到最后一个结点（即表尾）。

（3）将表尾结点的地址设置为新增结点的地址。

（4）将新增结点的地址部分设置为空地址NULL，即新增结点成为表尾。

示例代码如下：


代码如下:

CLType * CLAddEnd(CLType *head,Data nodeData)
{
 CLType *node,*htemp;
 if(!(node = new CLType))
 {
  cout<<"分配内存失败！"<<endl;  //分配内存失败
  return NULL;
 }
 else
 {
  node->nodeData = nodeData;   //保存结点数据
  node->nextNode = NULL;     //设置结点指针为空，即作为表尾
  if(head == NULL)      //当链表是空表的时候
  {
   head = node;
   return head;
  }
  htemp = head;
  while(htemp->nextNode != NULL)   //查找链表的末尾
  {
   htemp = htemp->nextNode; 
  }
  htemp->nextNode = node;
  return head;
 }

}

输入参数head为链表头指针，输入参数nodeData为结点保存的数据。程序中，使用new关键字申请动态空间，如果内分配成功，node中将保存指向该内存区域的指针。

然后，将传入的nodeData保存到申请的内存区域，并设置该结点指向下一结点的指针值为NULL。

插入头结点

插入头结点就是在链表首部添加结点的过程，和在表尾插入结点相反，这个操作是在表头上插入结点，作为头结点。

插入头结点的步骤如下：

（1）首先分配内存，保存新增的结点。

（2）使新增姐弟那指向头指针head所指向的结点

（3）然后使头指针head指向新增结点

示例代码如下：


代码如下:

CLType *CLAddFirst(CLType *head,Data nodeData)
{
 CLType *node;
 if(!(node = new CLType))
 {
  cout<<"分配内存失败"<<endl;
  return NULL;
 }
 else
 {
  node->nodeData = nodeData;  //保存结点数据
  node->nextNode = head;  //指向头指针所指向的指针
  head = node;   //头指针指向新增结点
  return head;
 }
}

输入参数head为链表头指针，输入参数nodeData为结点中保存的数据。程序中首先使用new关键字申请一个新的保存结点的内存空间，如果申请成功，node中将保存指向该内存区域的指针。

然后，将传入的nodeData保存到申请的内存区域中，并使新增的结点指向头指针head所指向的结点，然后设置头指针head重新指向新增结点。

查找结点

查找结点就是在链表结构中查找需要的元素。对于链表结构来说，一般可以分为按照结点序号查找和按照关键字查询两类。

按照结点序号查询

即查询链表中的第多少个结点，其示例代码如下：


代码如下:

CLType *CLFindNodeNum(CLType *head,int k)
{
 CLType *htemp;
 int i = 1;
 htemp = head;      //保存链表头指针
          for(i = 1;i<k&&htemp;i++)     //找到该结点
          {
        htemp = htemp->nextNode;
         }
          return htemp;      //返回指向第k个结点的指针
}

输入参数head为链表头指针，输入参数k为要查询的结点的序号。通过序号进行多次循环，获得指向该结点的指针，然后返回指针。

按照关键字查询

即根据链表中结点的某一个关键字进行查询，我们以查询学生的姓名（name）为例，其示例代码如下：


代码如下:

CLType *CLFindNodeKey(CLType *head,string name)
{
 CLType * htemp;
 htemp = head;       //保存链表头指针
 while(htemp)
 {
  if(htemp->nodeData.name == name) //当结点关键字和传入关键字相同
  {
   return htemp;    //返回该结点指针
  }
  htemp = htemp->nextNode;
 }
 return NULL;
}

输入参数head为链表头指针，输入参数name为要查询的同学的姓名。遍历查询所有的同学的姓名，当有结点的姓名与所查询的姓名相同的时候，则返回该结点的指针。

插入结点

插入结点就是在链表中间部分的位置增加一个结点。

插入结点的步骤如下：

（1）分配内存空间，保存新增的结点。

（2）找到要插入的逻辑位置，也就是找到插在那个结点的后面。

（3）修改插入位置结点的指针，使其指向新增结点，而使新增结点指向原插入位置所指向的结点。

示例代码如下：


代码如下:

CLType *CLInsertNode(CLType *head,int k,Data nodeData)
{
 CLType *node,*nodetemp;
 if(!(node = new CLType))    //申请结点
 {
  cout<<"申请内存失败"<<endl;
  return NULL;
 }
 else
 {
  node->nodeData = nodeData;  //保存结点中的数据
  nodetemp=CLFindNodeNum(head,k-1);//通过按照结点序号查找函数找到插入点前一个结点（关键结点）
  if(nodetemp)
  {
   node->nextNode = nodetemp->nextNode;//插入的结点指向关键结点的下一个节点
   nodetemp->nextNode = node;    //关键结点指向插入点
  }
  else
  {
   cout<<"没有找到正确的插入位置"<<endl;
   delete node;
  }
 }
 return head;      //返回头指针
}

输入参数head为链表头指针，输入参数findkey为链表中进行查找的结点关键字，找到该结点后将在该结点后面添加结点数据，nodeData为新增结点的数据。程序中首先使用new申请结点空间，然后调用CLFindNodeNum函数查找指向结点，然后执行插入操作。

删除结点

删除结点就是将链表中的某个结点数据删除，并不影响其位置前后的结点。

删除结点操作的步骤如下：

（1）查找需要删除的结点。

（2）使前一结点指向当前节点的下一结点。

（3）删除该结点

删除结点可以通过结点的序号确定要删除的结点，当然也可以通过结点的关键字确定要删除的结点。

我们以通过关键字删除结点为例，示例代码如下：


代码如下:

int CLDeleteNode(CLType *head,string name)
{
 CLType *node,*htemp;    //node用于删除结点的前一个结点
 htemp = head;
 node =  head;
 while(htemp)
 {
  if(htemp->nodeData.name == name)//找到关键字，执行删除操作
  {
   node->nextNode = htemp->nextNode;//使前一结点指向当前节点的下一结点
   delete htemp;     //释放该结点的空间（即，删除了结点）
   return 1;
  }
  else
  {
   node = htemp;     //指向当前节点
   htemp = htemp->nextNode;  //指向下一个结点
  }
 }
  return 0;        //删除失败
}

head为链表头指针，输入参数name表示要删除的同学的姓名。程序中，通过一个循环，按关键字在整个链表中查找要删除的结点。如果找到被删除的结点，则设置上一结点（node指针所指结点）指向当前结点（h指针所指结点）的下一个结点，即在逻辑上将该结点删除，然后对该结点执行delete操作，释放结点占用的内存空间，即在物理上将其删除。

计算链表长度

计算链表长度也就是统计链表中结点的数量。顺序表中计算链表长度比较方便，但在链表中链表的长度却需要通过遍历链表来获得，因为链表在物理上不是连续存储的。

示例代码如下：


代码如下:

int CLLength(CLType *head)
{
 CLType *htemp;
 int Len = 0;
 htemp = head;
 while(htemp)       //遍历整个数组
 {
  Len++;        //累加结点的数量
  htemp = htemp->nextNode;    //处理下一个结点
 }
 return Len;
}

参数head是链表的头指针，程序中通过while来遍历指针，Len作为计数器，通过记录循环的次数，来获得链表的长度，当指针为NULL时截止，然后返回计数器的值。

显示所有结点

遍历所有的结点，并输出。


代码如下:

void CLAllNode(CLType *head)
{
 CLType *htemp;
 htemp = head;
 while(htemp)       //遍历整个数组
 {
  nodeData = htemp->nodeData;   //获取结点数据
  cout<<"key:"<<nodeData.key<<",name:"<<nodeData.name<<",age:"<<nodeData.age<<endl;
  htemp = htemp->nextNode;    //处理下一个结点
 }
}

输出结点的函数，没有返回值，所有定义为void。每次都通过CLType类型的结点获得其nodeData的值

链表操作完整示例

完整示例的代码比较长，要耐心看哈……  :)


代码如下:

#include<iostream>
#include<string>
using namespace std;
struct Data   //数据结点类型
{
 string key;  //关键字
 string name;
 int age;
};
struct CLType          //定义链表结构
{
 Data nodeData;
 CLType *nextNode;
};
CLType * CLAddEnd(CLType *head,Data nodeData)
{
 CLType *node,*htemp;
 if(!(node = new CLType))
 {
  cout<<"分配内存失败！"<<endl;  //分配内存失败
  return NULL;
 }
 else
 {
  node->nodeData = nodeData;         //保存结点数据
  node->nextNode = NULL;   //设置结点指针为空，即作为表尾
  if(head == NULL)   //当链表是空表的时候
  {
   head = node;
   return head;
  }
  htemp = head;
  while(htemp->nextNode != NULL) //查找链表的末尾
  {
   htemp = htemp->nextNode; 
  }
  htemp->nextNode = node;
  return head;
 }

}
CLType *CLAddFirst(CLType *head,Data nodeData)
{
 CLType *node;
 if(!(node = new CLType))
 {
  cout<<"分配内存失败"<<endl;
  return NULL;
 }
 else
 {
  node->nodeData = nodeData;  //保存结点数据
  node->nextNode = head;  //指向头指针所指向的指针
  head = node;   //头指针指向新增结点
  return head;
 }
}
CLType *CLFindNodeNum(CLType *head,int k)
{
 CLType *htemp;
 int i = 1;
 htemp = head;    //保存链表头指针
    for(i = 1;i<k&&htemp;i++)   //找到该结点
    {
     htemp = htemp->nextNode;
    }
    return htemp;     //返回指向第k个结点的指针
}
CLType *CLFindNodeName(CLType *head,string name)
{
 CLType * htemp;
 htemp = head;    //保存链表头指针
 while(htemp)
 {
  if(htemp->nodeData.name == name) //当结点关键字和传入关键字相同
  {
   return htemp;  //返回该结点指针
  }
  htemp = htemp->nextNode;
 }
 return NULL;
}
CLType *CLInsertNode(CLType *head,int k,Data nodeData)
{
 CLType *node,*nodetemp;
 if(!(node = new CLType))   //申请结点
 {
  cout<<"申请内存失败"<<endl;
  return NULL;
 }
 else
 {
  node->nodeData = nodeData;  //保存结点中的数据
  nodetemp=CLFindNodeNum(head,k-1);    //通过按照结点序号查找函数找到插入点前一个结点（关键结点）
  if(nodetemp)
  {
   node->nextNode = nodetemp->nextNode;  //插入的结点指向关键结点的下一个节点
   nodetemp->nextNode = node;    //关键结点指向插入点
  }
  else
  {
   cout<<"没有找到正确的插入位置"<<endl;
   delete node;
  }
 }
 return head;      //返回头指针
}
int CLDeleteNode(CLType *head,string name)
{
 CLType *node,*htemp;    //node用于删除结点的前一个结点
 htemp = head;
 node =  head;
 while(htemp)
 {
  if(htemp->nodeData.name == name)             //找到关键字，执行删除操作
  {
   node->nextNode = htemp->nextNode;  //使前一结点指向当前节点的下一结点
   delete htemp;   //释放该结点的空间（即，删除了结点）
   return 1;
  }
  else
  {
   node = htemp;   //指向当前节点
   htemp = htemp->nextNode;  //指向下一个结点
  }
 }
  return 0;     //删除失败
}
int CLLength(CLType *head)
{
 CLType *htemp;
 int Len = 0;
 htemp = head;
 while(htemp)     //遍历整个数组
 {
  Len++;     //累加结点的数量
  htemp = htemp->nextNode;    //处理下一个结点
 }
 return Len;
}
void CLAllNode(CLType *head)
{
 CLType *htemp;
 Data nodeData;
 htemp = head;
 cout<<"链表长度为："<<CLLength(head)<<endl;
 while(htemp)     //遍历整个数组
 {
  nodeData = htemp->nodeData;   //获取结点数据
  cout<<"key:"<<nodeData.key<<",name:"<<nodeData.name<<",age:"<<nodeData.age<<endl;
  htemp = htemp->nextNode;    //处理下一个结点
 }
}
int main()
{
 CLType *node,*head = NULL;
 Data nodeData;
 string name;
 int k;
 cout<<"请先输入链表中的数据，格式为：学号，姓名，年龄（年龄为0时停止输入）"<<endl;
 while(1)
 {
  cin>>nodeData.key>>nodeData.name>>nodeData.age;
  if(nodeData.age==0)break;
  head=CLAddEnd(head,nodeData);  //在链表的尾部添加结点
 }
 CLAllNode(head);     //显示所有的结点
 //演示在头部插入数据
 cout<<"请输入一个结点，并在链表的头部插入"<<endl;
 cin>>nodeData.key>>nodeData.name>>nodeData.age;
 head=CLAddFirst(head,nodeData);
 CLAllNode(head);
 //演示在中间位置插入一个数据
 cout<<"请输入一个在链表内部插入的结点："<<endl;
 cin>>nodeData.key>>nodeData.name>>nodeData.age;
 cout<<"请输入插入点的位置：";
 cin>>k;
 head=CLInsertNode(head,k,nodeData);
 CLAllNode(head); 
 //演示按照序号查询数据
 cout<<"请输入按照结点查询的一个结点序号：";
 cin>>k;
 node=CLFindNodeNum(head,k);
 cout<<"您所查询的结点是："<<endl;
 cout<<"key:"<<node->nodeData.key<<",name:"<<node->nodeData.name<<",age:"<<node->nodeData.age<<endl;
 //演示按照姓名查询数据
 cout<<"请输入一个按照姓名查询的一个同学的姓名：";
 cin>>name;
 node=CLFindNodeName(head,name);
 cout<<"您所查询的结点是："<<endl;
 cout<<"key:"<<node->nodeData.key<<",name:"<<node->nodeData.name<<",age:"<<node->nodeData.age<<endl;
 //演示删除数据信息
 cout<<"请输入结点中的一个同学中的名字，系统会删除他的信息：";
 cin>>name;
 if(CLDeleteNode(head,name))cout<<"数据删除成功！"<<endl;
 CLAllNode(head);
 return 0;
}

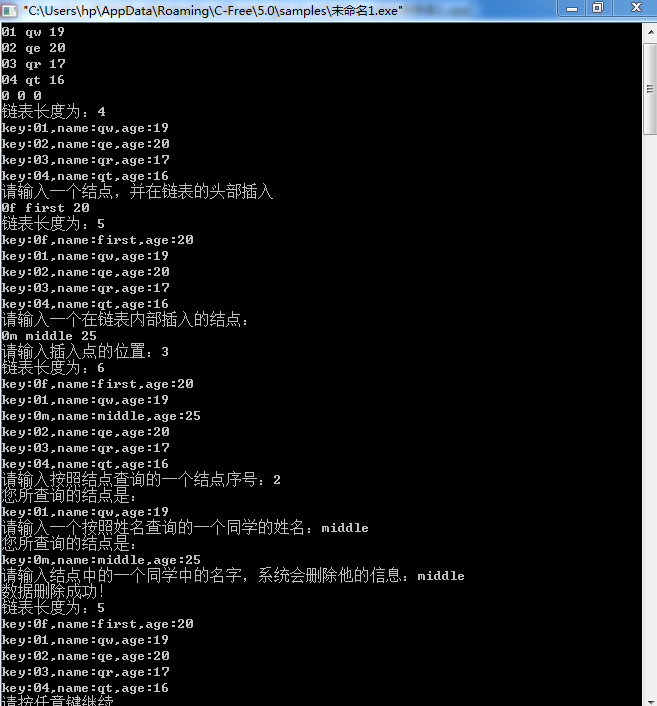
程序运行结果示例：