Python求正态分布曲线下面积实例

正态分布应用最广泛的连续概率分布，其特征是“钟”形曲线。这种分布的概率密度函数为：

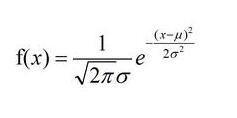
其中，μ为均值，σ为标准差。

求正态分布曲线下面积有3σ原则:

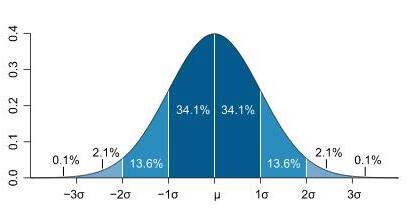
正态曲线下，横轴区间（μ-σ，μ+σ）内的面积为68.268949%，横轴区间（μ-1.96σ，μ+1.96σ）内的面积为95.449974%，横轴区间（μ-2.58σ，μ+2.58σ）内的面积为99.730020%。

求任意区间内曲线下的面积，通常可以引用scipy包中的相关函数

norm函数生成一个给定均值和标准差的正态分布，cdf(x)表示－∞到x的概率

例：(2，1)正态分布下 2-3曲线下的面积

>>> import scipy.stats
>>> scipy.stats.norm(2,1).cdf(3)-0.5
0.34134474606854293

由于有时候不便于引用scipy包，自编这一函数也很简单

求积分函数参考：复化梯形求积分

cdfd(a,b,u,o)

a,b 为区间起始范围，u，o分别为正态分布的均值和标准差。

import math

def pdf(x):
  return math.exp(-(x) ** 2 / (2)) / (math.sqrt(2 * math.pi))

def sum_fun_xk(xk, func):
  return sum([func(each) for each in xk])

def integral(a, b, n, func):
  h = (b - a)/float(n)
  xk = [a + i*h for i in range(1, n)]
  return h/2 * (func(a) + 2 * sum_fun_xk(xk, func) + func(b))

def cdfd(a,b,u,o):
  return integral((a-u)/o,(b-u)/o,10000,pdf)

cdfd(2,3,2,1)

Out: 0.3413399854638336

以上这篇Python求正态分布曲线下面积实例就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。

赞 (0)

相关推荐

  • Python数据可视化实现正态分布（高斯分布）

    正态分布(Normal distribution)又成为高斯分布(Gaussian distribution) 若随机变量X服从一个数学期望为.标准方差为的高斯分布,记为: 则其概率密度函数为: 正态分布的期望值决定了其位置,其标准差决定了分布的幅度.因其曲线呈钟形,因此人们又经常称之为钟形曲线.我们通常所说的标准正态分布是的正态分布: 概率密度函数 代码实现: # Python实现正态分布 # 绘制正态分布概率密度函数 u = 0 # 均值μ u01 = -2 sig = math.sqrt(

  • 在python中画正态分布图像的实例

    1.正态分布简介 正态分布(normal distribtution)又叫做高斯分布(Gaussian distribution),是一个非常重要也非常常见的连续概率分布.正态分布大家也都非常熟悉,下面做一些简单的介绍. 假设随机变量XX服从一个位置参数为μμ.尺度参数为σσ的正态分布,则可以记为: 而概率密度函数为 2.在python中画正态分布直方图 先直接上代码 import numpy as np import matplotlib.mlab as mlab import matplot

  • 使用python绘制3维正态分布图的方法

    今天使用python画了几个好玩的3D展示图,现在分享给大家. 先贴上图片 使用的python工具包为: from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D 在贴代码之前,有必要从整体上了解这些图是如何画出来的.可以把上面每一个3D图片理解成一个长方体.输入数据是三维的,x轴y轴和z轴.在第三个图片里面有x.y和z坐标的标识.在第三张图片中,我们可以理解为,

  • Python使用numpy产生正态分布随机数的向量或矩阵操作示例

    Python使用numpy产生正态分布随机数的向量或矩阵操作示例

    本文实例讲述了Python使用numpy产生正态分布随机数的向量或矩阵操作.分享给大家供大家参考,具体如下: 简单来说,正态分布(Normal distribution)又名高斯分布(Gaussian distribution),是一个在数学.物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力.一般的正态分布可以通过标准正态分布配合数学期望向量和协方差矩阵得到.如下代码,可以得到满足一维和二维正态分布的样本. 示例1(一维正态分布): # coding=utf-8 '''

  • Python求解正态分布置信区间教程

    正态分布和置信区间 正态分布(Normal Distribution)又叫高斯分布,是一种非常重要的概率分布.其概率密度函数的数学表达如下: 置信区间是对该区间能包含未知参数的可置信的程度的描述. 使用SciPy求解置信区间 import numpy as np import matplotlib.pyplot as plt from scipy import stats N = 10000 x = np.random.normal(0, 1, N) # ddof取值为1是因为在统计学中样本的标

  • Python数据可视化正态分布简单分析及实现代码

    Python数据可视化正态分布简单分析及实现代码

    Python说来简单也简单,但是也不简单,尤其是再跟高数结合起来的时候... 正态分布(Normaldistribution),也称"常态分布",又名高斯分布(Gaussiandistribution),最早由A.棣莫弗在求二项分布的渐近公式中得到.C.F.高斯在研究测量误差时从另一个角度导出了它.P.S.拉普拉斯和高斯研究了它的性质.是一个在数学.物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力. 正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人

  • 使用Python实现正态分布、正态分布采样

    多元正态分布(多元高斯分布) 直接从多元正态分布讲起.多元正态分布公式如下: 这就是多元正态分布的定义,均值好理解,就是高斯分布的概率分布值最大的位置,进行采样时也就是采样的中心点.而协方差矩阵在多维上形式较多. 协方差矩阵 一般来说,协方差矩阵有三种形式,分别称为球形.对角和全协方差.以二元为例: 为了方便展示不同协方差矩阵的效果,我们以二维为例.(书上截的图,凑活着看吧,是在不想画图了) 其实从这个图上可以很好的看出,协方差矩阵对正态分布的影响,也就很好明白了这三个协方差矩阵是哪里来的名字了

  • Python求正态分布曲线下面积实例

    正态分布应用最广泛的连续概率分布,其特征是"钟"形曲线.这种分布的概率密度函数为: 其中,μ为均值,σ为标准差. 求正态分布曲线下面积有3σ原则: 正态曲线下,横轴区间(μ-σ,μ+σ)内的面积为68.268949%,横轴区间(μ-1.96σ,μ+1.96σ)内的面积为95.449974%,横轴区间(μ-2.58σ,μ+2.58σ)内的面积为99.730020%. 求任意区间内曲线下的面积,通常可以引用scipy包中的相关函数 norm函数生成一个给定均值和标准差的正态分布,cdf(x

  • python求加权平均值的实例(附纯python写法)

    首先是数据源: #需要求加权平均值的数据列表 elements = [] #对应的权值列表 weights = [] 使用numpy直接求: import numpy as np np.average(elements, weights=weights) 附纯python写法: # 不使用numpy写法1 round(sum([elements[i]*weights[i] for i in range(n)])/sum(weights), 1) # 不使用numpy写法2 round(sum([

  • python求众数问题实例

    本文实例讲述了python求众数问题的方法,是一个比较典型的应用.分享给大家供大家参考.具体如下: 问题描述: 多重集中重数最大的元素称为众数...就是一个可以有重复元素的集合,在这个集合中重复的次数最多的那个数就叫它的众数... 如S = [1,2,2,2,3,5] 重数是2,其重数为3 实例代码如下: list_num = [] list_num_count = 0 dict_num ={} #从文件读入,文件第一行为集合中元素的个数,以后每一行为一个元素 list_num_count =

  • python 求1-100之间的奇数或者偶数之和的实例

    如下所示: i=0 sum1=0 sum2=0 while i<=100: if i%2==0: sum1+=i else: sum2+=i i+=1 print('1-100之间偶数和为:%d' % sum1) print('1-100之间偶数和为:%d' % sum2) 结果: 1-100之间偶数和为:2550 1-100之间奇数和为:2500 以上这篇python 求1-100之间的奇数或者偶数之和的实例就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持我们.

  • python 求一个列表中所有元素的乘积实例

    如下所示: # 求一个列表中所有元素的乘积 from functools import reduce lt = [1,2,3,4,5] ln = reduce(lambda x,y:x * y,lt) print(ln) 以上这篇python 求一个列表中所有元素的乘积实例就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持我们.

  • Python求均值,方差,标准差的实例

    如下所示: import numpy as np arr = [1,2,3,4,5,6] #求均值 arr_mean = np.mean(arr) #求方差 arr_var = np.var(arr) #求标准差 arr_std = np.std(arr,ddof=1) print("平均值为:%f" % arr_mean) print("方差为:%f" % arr_var) print("标准差为:%f" % arr_std) 以上这篇Pyth

  • Python根据欧拉角求旋转矩阵的实例

    利用numpy和scipy,我们可以很容易根据欧拉角求出旋转矩阵,这里的旋转轴我们你理解成四元数里面的旋转轴 import numpy as np import scipy.linalg as linalg import math #参数分别是旋转轴和旋转弧度值 def rotate_mat(self, axis, radian): rot_matrix = linalg.expm(np.cross(np.eye(3), axis / linalg.norm(axis) * radian)) a

  • Python 求数组局部最大值的实例

    求数组局部最大值 给定一个无重复元素的数组A[0-N-1],求找到一个该数组的局部最大值.规定:在数组边界外的值无穷小.即:A[0]>A[-1],A[N-1] >A[N]. 显然,遍历一遍可以找到全局最大值,而全局最大值显然是局部最大值. 可否有更快的办法? 算法描述 使用索引left.right分别指向数组首尾. 求中点 mid = ( left + right ) / 2 A[mid]>A[mid+1],丢弃后半段:right=mid A[mid+1]>A[mid],丢弃前半段

  • python 求10个数的平均数实例

    一,已知十个数,求平均数. L=[1,2,3,4,5,6,7,8,9,10] a=sum(L)/len(L) print("avge is:", round(a,3) ) 运行结果: avge is: 5.5 二,设置输入个数,求平均数 n = int(input("请输入所求平均数的个数: ")) l = [] for i in range(0, n): k = int(input("请输入数值: ")) l.append(k) avg = s

  • python求前n个阶乘的和实例

    我就废话不多说了,还是直接看代码吧! i = int(input("input")) sum = 0 if i<1: exit() else: while i>0: b = 2 c = 1 while b<=i: c=b*c b=b+1 sum += c i = i-1 # print(c) print(sum) 补充知识:python 利用递归方法求解n的阶乘和 写程序算出n的阶乘的和 def fn(x): if x==1: return 1 def f(x): i

随机推荐