Java数据结构之图的基础概念和数据模型详解
目录
- 图的实际应用
- 图的定义及分类
- 图的相关术语
- 图的存储结构
- 邻接矩阵
- 邻接表
- 图的实现
- 图的API设计
- 代码实现
图的实际应用
在现实生活中,有许多应用场景会包含很多点以及点点之间的连接,而这些应用场景我们都可以用即将要学习的图这种数据结构去解决。
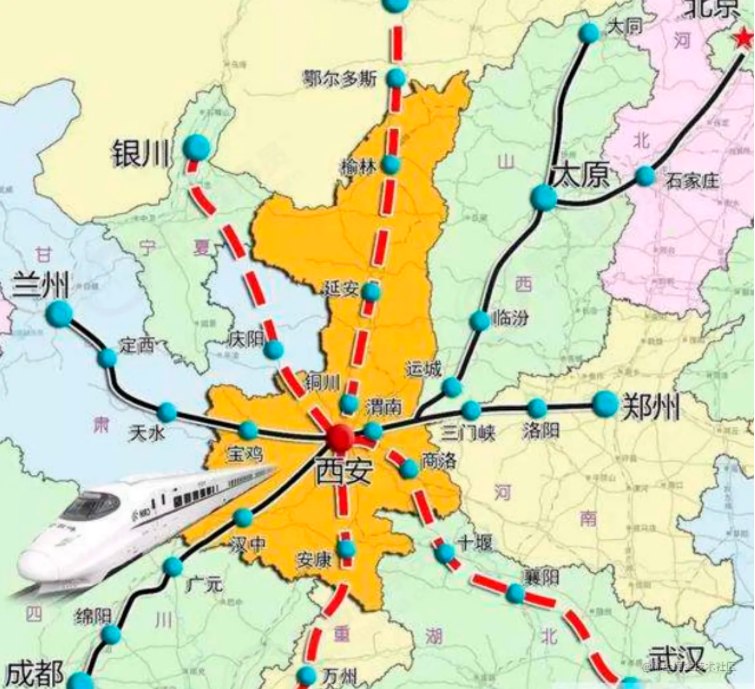
地图:
我们生活中经常使用的地图,基本上是由城市以及连接城市的道路组成,如果我们把城市看做是一个一个的点,把道路看做是一条一条的连接,那么地图就是我们将要学习的图这种数据结构。
图的定义及分类
定义: 图是由一组顶点和一组能够将两个顶点相连的边组成的。
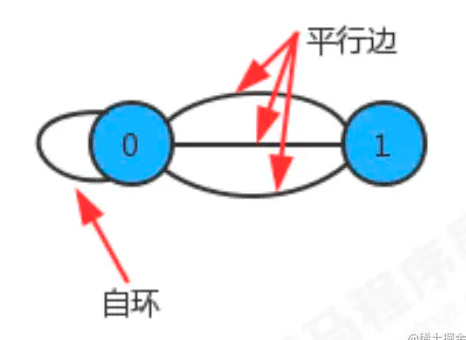
特殊的图:
- 自环:即一条连接一个顶点和其自身的边;
- 平行边:连接同一对顶点的两条边;
图的分类:
按照连接两个顶点的边的不同,可以把图分为以下两种:
无向图:边仅仅连接两个顶点,没有其他含义;
有向图:边不仅连接两个顶点,并且具有方向;
图的相关术语
相邻顶点:
当两个顶点通过一条边相连时,我们称这两个顶点是相邻的,并且称这条边依附于这两个顶点。
度:
某个顶点的度就是依附于该顶点的边的个数
子图:
是一幅图的所有边的子集(包含这些边依附的顶点)组成的图;
路径:
是由边顺序连接的一系列的顶点组成
环:
是一条至少含有一条边且终点和起点相同的路径
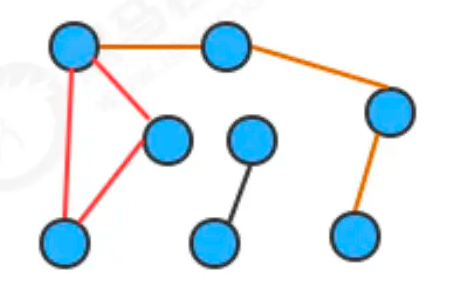
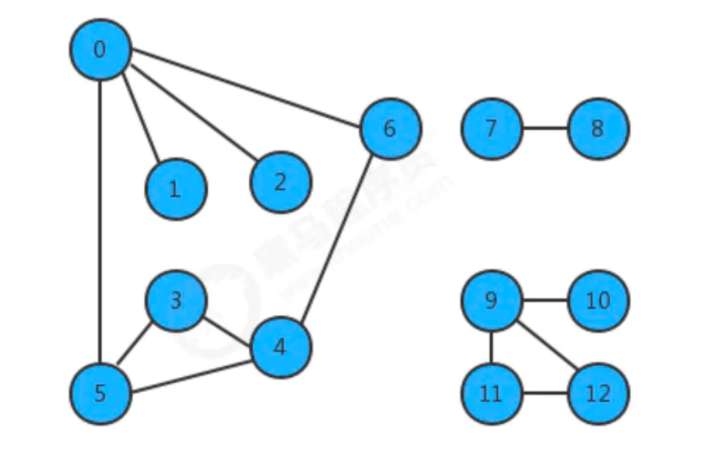
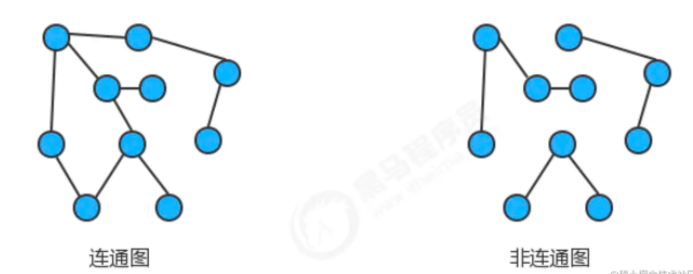
连通图:
如果图中任意一个顶点都存在一条路径到达另外一个顶点,那么这幅图就称之为连通图
连通子图:
一个非连通图由若干连通的部分组成,每一个连通的部分都可以称为该图的连通子图
图的存储结构
要表示一幅图,只需要表示清楚以下两部分内容即可:
- 图中所有的顶点;
- 所有连接顶点的边;
常见的图的存储结构有两种:邻接矩阵和邻接表。
邻接矩阵
- 使用一个V*V的二维数组int[V][V] adj,把索引的值看做是顶点;
- 如果顶点v和顶点w相连,我们只需要将adj[v][w]和adj[w][v]的值设置为1,否则设置为0即可。
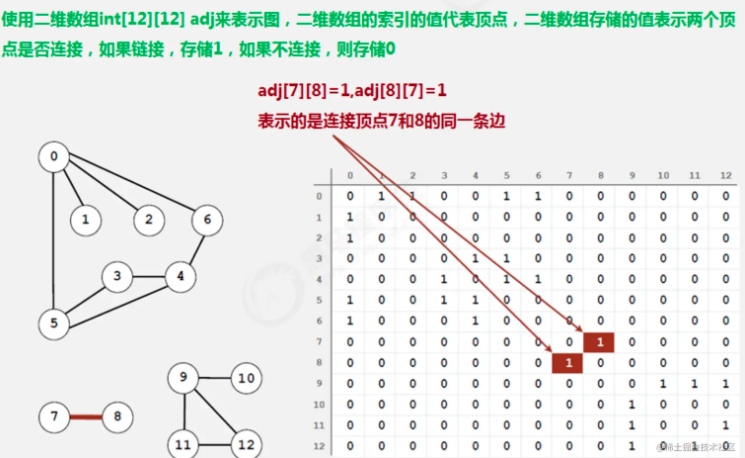
很明显,邻接矩阵这种存储方式的空间复杂度是V^2的,如果我们处理的问题规模比较大的话,内存空间极有可能不够用。
邻接表
1.使用一个大小为V的数组 Queue[V] adj,把索引看做是顶点;
2.每个索引处adj[v]存储了一个队列,该队列中存储的是所有与该顶点相邻的其他顶点。
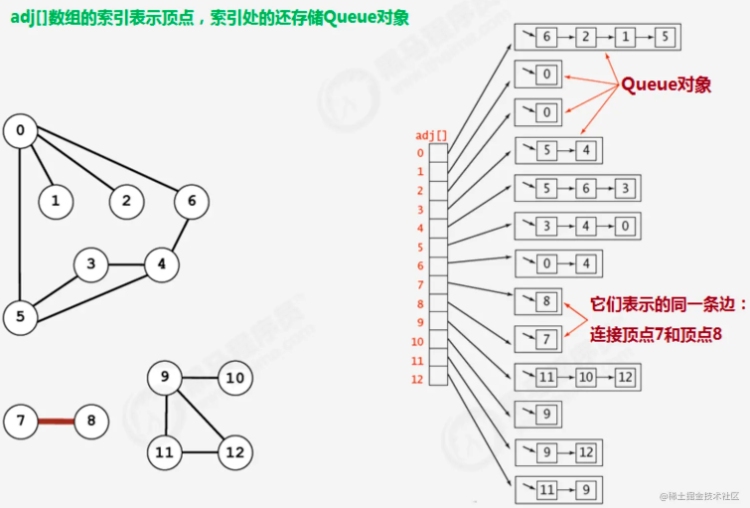
很明显,邻接表的空间并不是是线性级别的,所以后面我们一直采用邻接表这种存储形式来表示图。
图的实现
下面通过代码实现一个无向图。
图的API设计
| 类名 | Graph |
|---|---|
| 成员变量 | 1.private final int V: 记录顶点数量2.private int E: 记录边数量3.private Queue[] adj: 邻接表 |
| 构造方法 | Graph(int V):创建一个包含V个顶点但不包含边的图 |
| 成员方法 | 1.public int V():获取图中顶点的数量2.public int E():获取图中边的数量3.public void addEdge(int v,int w):向图中添加一条边 v-w4.public Queue adj(int v):获取和顶点v相邻的所有顶点 |
代码实现
/**
* 无向图的表示
*
* @author alvin
* @date 2022/10/30
* @since 1.0
**/
public class Graph {
//顶点数目
private final int V;
//边的数目
private int E;
//邻接表,队列的形式
private Queue<Integer>[] adj;
public Graph(int V) {
// 初始化顶点数量
this.V = V;
//初始化边的数量
this.E = 0;
//初始化邻接表
this.adj = new Queue[V];
//初始化邻接表中的空队列
for (int i = 0; i < adj.length; i++) {
adj[i] = new ArrayDeque<>();
}
}
public void addEdge(int v, int w) {
//把w添加到v的链表中,这样顶点v就多了一个相邻点w
adj[v].add(w);
//把v添加到w的链表中,这样顶点w就多了一个相邻点v
adj[w].add(v);
//边的数目自增1
E++;
}
//获取顶点数目
public int V() {
return V;
}
//获取边的数目
public int E(){
return E;
}
//获取和顶点v相邻的所有顶点
public Queue<Integer> adj(int v) {
return adj[v];
}
}
数组adj的索引表示顶点。
到此这篇关于Java数据结构之图的基础概念和数据模型详解的文章就介绍到这了,更多相关Java数据结构 图内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们!

